Pythonで順列、組合せの計算をする

Pythonで順列、組合の配列を作成します。

順列

重複順列のリストを作成し個数を計算する

ユーザー定義関数による方法

\begin{eqnarray*} M_X(t)&=&E(\mathrm{e}^{tk})\\ &=&\sum_{k=0}^{n}\mathrm{e}^{tk}P(X=k)\\ &=&\sum_{k=0}^{n}\mathrm{e}^{tk}\begin{pmatrix}n \\ k\end{pmatrix} p^{k}{(1-p)}^{n-k}\\ &=&\sum_{k=0}^{n}\mathrm{e}^{tk}\ _n C_k p^{k}{(1-p)}^{n-k}\\ &=&\sum_{k=0}^{n}\ _n C_k {(\mathrm{e}^tp)}^{k}{(1-p)}^{n-k}\\ &=&{(\mathrm{e}^tp+1-p)}^n \end{eqnarray*}

\begin{eqnarray*} \left(\int_0^{\infty} e^{-x^2} d x\right)^2 & =\int_0^{\infty} e^{-x^2} d x \int_0^{\infty} e^{-y^2} d y\tag{1} \\ &=\int_0^{\infty} \int_0^{\infty} e^{-\left(x^2+y^2\right)} d x d y \end{eqnarray*} \begin{eqnarray*}m_X(t)&=&E(\mathrm{e}^{tX})\\ &=&\displaystyle \int_{ – \infty }^{ \infty }\mathrm{e}^{tx}f(x)dx\\ &=&\displaystyle \int_{ – \infty }^{ \infty }\frac{1}{\sqrt{2πσ^2}}\exp{[-\frac{(x-\mu)^2}{2σ^2}+tx]}dx\\ &=&\displaystyle \int_{ – \infty }^{ \infty }\frac{1}{\sqrt{2πσ^2}}\exp{[-\frac{1}{2σ^2}(x^2-2\mu x+{\mu}^{2}-2{\sigma}^{2}tx)]}dx\\ &=&\displaystyle \int_{ – \infty }^{ \infty }\frac{1}{\sqrt{2πσ^2}}\exp{[-\frac{1}{2σ^2}({(x-(\mu+{\sigma}^{2}t))}^{2}+2\mu{\sigma}^{2}t+{\sigma}^{4}t^{2})]}dx\\ &=&\displaystyle \int_{ – \infty }^{ \infty }\frac{1}{\sqrt{2πσ^2}}\exp{[-\frac{(x-(\mu+{\sigma}^{2}t))^2}{2σ^2}+\mu t+\frac{{\sigma}^{2}t^2}{2}]}dx\\ &=&{\mathrm{e}}^{\mu t+\frac{{\sigma}^{2}t^2}{2}}\displaystyle \int_{ – \infty }^{ \infty }\frac{1}{\sqrt{2πσ^2}}\exp{[-\frac{(x-(\mu+{\sigma}^{2}t))^2}{2σ^2}]}dx\\ &=&{\mathrm{e}}^{\mu t+\frac{{\sigma}^{2}t^2}{2}}\end{eqnarray*} \begin{eqnarray*} & \int_0^1\left(\_n C_0+\_n C_1 x+\_n C_2 x^2+\cdots \cdots+\_n C_n x^n\right) d x \\ & =\left[\_n C_0 x+\frac{\_n C_1}{2} x^2+\frac{\_n C_2}{3} x^3+\cdots \cdots+\frac{\_n C_n}{n+1} x^{n+1}\right]_0^1 \\ & =\_n C_0+\frac{\_n C_1}{2}+\frac{\_n C_2}{3}+\cdots \cdots+\frac{\_n C_n}{n+1} \\ & \therefore \quad \frac{\mathbf{2}^{\boldsymbol{n}+1}-\mathbf{1}}{\boldsymbol{n}+\mathbf{1}}=\_n C_{\mathbf{0}}+\frac{\_{\boldsymbol{n}} C_{\mathbf{1}}}{f\mathbf{2}}+\frac{\_{\boldsymbol{n}} C_{\mathbf{2}}}{\mathbf{3}}+\cdots+\frac{\_n C_{\boldsymbol{n}}}{\boldsymbol{n}+\mathbf{1}} \end{eqnarray*}

まず、すべての基本となる重複順列のリストを作成します。リンゴ、ミカン、バナナの3種類のくだものを0日目、1日目、2日目の3日に分けて受け取ることを考えます。このとき、それぞれのくだもの数は十分にあり、リンゴの好きな人は3日ともリンゴを選ぶこともできます。すべての組み合わせをリストであらわすプログラムを作成します。ここでは、n種類のくだものから、r日間もらえるので、すべての組み合わせは$n^r$とおりとなります。このことも確認してみます。

重複順列　(sequence with repetition)

product = [[]]
r = 3
n_list = ['リンゴ', 'ミカン', 'バナナ']
for _ in range(r):
temp = product
product = []
for elm in temp:
for fruit in n_list:
product.append(elm + [fruit])
pprint.pprint(product)
print(f'リストの個数:{len(product)},　nのr乗：{len(n_list)**r}')

[['リンゴ', 'リンゴ', 'リンゴ'],
 ['リンゴ', 'リンゴ', 'ミカン'],
 ['リンゴ', 'リンゴ', 'バナナ'],
 ['リンゴ', 'ミカン', 'リンゴ'],
 ['リンゴ', 'ミカン', 'ミカン'],
 ['リンゴ', 'ミカン', 'バナナ'],
 ['リンゴ', 'バナナ', 'リンゴ'],
 ['リンゴ', 'バナナ', 'ミカン'],
 ['リンゴ', 'バナナ', 'バナナ'],
 ['ミカン', 'リンゴ', 'リンゴ'],
 ['ミカン', 'リンゴ', 'ミカン'],
 ['ミカン', 'リンゴ', 'バナナ'],
 ['ミカン', 'ミカン', 'リンゴ'],
 ['ミカン', 'ミカン', 'ミカン'],
 ['ミカン', 'ミカン', 'バナナ'],
 ['ミカン', 'バナナ', 'リンゴ'],
 ['ミカン', 'バナナ', 'ミカン'],
 ['ミカン', 'バナナ', 'バナナ'],
 ['バナナ', 'リンゴ', 'リンゴ'],
 ['バナナ', 'リンゴ', 'ミカン'],
 ['バナナ', 'リンゴ', 'バナナ'],
 ['バナナ', 'ミカン', 'リンゴ'],
 ['バナナ', 'ミカン', 'ミカン'],
 ['バナナ', 'ミカン', 'バナナ'],
 ['バナナ', 'バナナ', 'リンゴ'],
 ['バナナ', 'バナナ', 'ミカン'],
 ['バナナ', 'バナナ', 'バナナ']]
リストの個数:27,　nのr乗：27

4.のforループの中で、リストsequenceにくだものを追加していきます。

5.リストsequenceを順次読みながらそのものを変更するのは難しいので、いったんsequenceを一時的にtempにコピーし、6.でsequenceを空にしてから、順次処理をしていきます。

9.でこれまで作ったリストに、さらにくだものを追加しています。

重複組み合わせは、くだものがたくさんあることを前提としているので、選択する数：rをくだものの数：3より少なくするだけでなく、多くすることもできます。また3.でn_list=range(3)とすることにより、くだものではなく0,1,2のように数字として一般化することできます。

重複組み合わせは、ギリシア文字のΠを使って次のように表現します。

重複順列　(sequence with repetition),

$\ _n\mathrm{\Pi}\ _r = n^r$

モジュールを使った重複順列の計算

itertoolsモジュールで重複順列の配列を生成する

重複順列はitertoolsモジュールを使って表示することもできます。

itertoolsモジュールによる方法

import itertools
list(itertools.product(['リンゴ','ミカン','バナナ'],repeat=3))

[('リンゴ', 'リンゴ', 'リンゴ'),
 ('リンゴ', 'リンゴ', 'ミカン'),
 ('リンゴ', 'リンゴ', 'バナナ'),
 ('リンゴ', 'ミカン', 'リンゴ'),
・・・(中略)
('バナナ', 'バナナ', 'ミカン'),
 ('バナナ', 'バナナ', 'バナナ')]

意味するところは#1と同じですが、1つの組み合わせはタプルになるところが相違点です。

順列のリストを作成し個数を計算する

順列のリストの作成とその個数を計算します。順列は、重複順列とは異なり、各自どのくだものも1回しか選ぶことができません。つまり、いくらリンゴが好きでも1日しか選ぶことができず、他の日はミカンとバナナを1回ずつしか選ぶことができません。数式にすると次のようになります。

順列(permutation)

考え方

$1 \leqq x_1\ne x_2\ne \cdots \ne x_k \leqq n$

順列の個数の計算

$\displaystyle {}_n\mathrm{P}_r = \frac{n!}{(n-r)!}=\overbrace {n(n-1)(n-2)・・・(n-r+1) \quad}^{r個}$

上記の式にもとづき、nこの中からr個を選ぶ順列の数を計算する関数を作成します。

順列の個数を計算する

def nPr(n,r):
npr=1
for i in range(n,n-r,-1):
npr*=i
return npr
nPr(3,2)

2.　変数nprで個数を計算します。次々と掛け算していく場合には、0ではなく1で初期化します。

3.　n,n-1・・・n-r+1まで逆にループするときには、3番目の引数は-1、また「まで」を示す2番目の引数はまでの値-1の値を指定します。この場合は(n-r+1)-1=n+rになります。

順列のリストを生成する

permutation = [[]]
n_list = ['リンゴ','ミカン','バナナ']
r=3
for _ in range(r):
temp=permutation
permutation=[]
for elm in temp:
for fruit in n_list:
if fruit not in elm:
permutation.append(elm + [fruit])
pprint.pprint(permutation)
print(f'リストの個数:{len(permutation)},　nPr：{math.factorial(len(n_list))}')

[['リンゴ', 'ミカン', 'バナナ'],
 ['リンゴ', 'バナナ', 'ミカン'],
 ['ミカン', 'リンゴ', 'バナナ'],
 ['ミカン', 'バナナ', 'リンゴ'],
 ['バナナ', 'リンゴ', 'ミカン'],
 ['バナナ', 'ミカン', 'リンゴ']]
リストの個数:6,　nPr：6

#1とほぼ同じですが、8.ですでに選ばれてリストにあるものと重複した場合には、新しいリストに入れないようにしています。

モジュールを使った順列の計算

順列の計算

順列にはいろいろなモジュールで個数や配列を求めることができます。

scipy.special関数による順列の数の計算

from scipy.special import perm
perm(3,3)

6.0

pythonのバージョンが3.8以上mathモジュールでも順列の個数を計算することができます。

mathモジュールによる順列の計算

import math
math.perm(5,3)

itertoolsで順列を生成する

itertoolsでは順列も生成することができます。

itertoolsツールによる順列の生成

import itertools
list(itertools.permutations(['リンゴ','ミカン','バナナ'],3))

[('リンゴ', 'ミカン', 'バナナ'),
 ('リンゴ', 'バナナ', 'ミカン'),
 ('ミカン', 'リンゴ', 'バナナ'),
 ('ミカン', 'バナナ', 'リンゴ'),
 ('バナナ', 'リンゴ', 'ミカン'),
 ('バナナ', 'ミカン', 'リンゴ')]

簡単に順列の配列を作ることができます。ここでは、個々の順列はtuppleになります。

組合せ

組み合わせの個数を計算し、配列を生成する

組み合わせは、順列に対し順序を気にしないで選ぶ方法です。数式にすると次の通りになります。

組み合わせ (combinations)

考え方

$1 \leqq x_1\lt x_2\lt \cdots \lt x_k \leqq n$

順列の個数の計算

$\displaystyle {}_n \mathrm{C}_r =\frac{_n \mathrm{P} _r}{r!}=\frac{n!}{r!(n-r)!}= \frac{\overbrace {n(n-1)(n-2)\cdots (n-r+1)}^{r個}}{\underbrace {r\times (r-1)\times \cdots 2 \times 1}_{r個}}$

組み合わせの個数を計算する

def nCr(n,r):
factr =1
r = min(r, n-r)
for i in range(r,1,-1):
factr*=i
return nPr(n,r)//factr
nCr(3,2)

6.　組み合わせの個数の計算をすると、分子の個数と分母の個数が同じr個で、なおかつ分母はrから1まで連続しているので、分子のr個の中には分母の数の倍数が含まれているはずです。つまり、組み合わせの数は必ず整数になるので、//演算子を使い整数に変換します。

組み合わせの配列の生成

n_list= ['リンゴ','ミカン','バナナ']
combination=[[item] for item in n_list]
r=2
for _ in range(r-1):
temp=combination
combination=[]
for elm in temp:
for i in range(n_list.index(elm[-1])+1,len(n_list)): #+1
combination.append(elm+[n_list[i]])
pprint.pprint(combination)
print(len(combination),nCr(len(n_list),r))
print(f'リストの個数:{len(combination)},　nCr：{nCr(len(n_list),r)}')

[['リンゴ', 'ミカン'], ['リンゴ', 'バナナ'], ['ミカン', 'バナナ']]
3 3
リストの個数:3,　nCr：3

モジュールによる順列の個数の計算と配列の生成

itertoolsでは順列も生成することができます。

itertoolsによる組み合わせの生成

import itertools
list(itertools.combinations(['リンゴ','ミカン','バナナ','カキ'],r=3))

[('リンゴ', 'ミカン', 'バナナ'),
 ('リンゴ', 'ミカン', 'カキ'),
 ('リンゴ', 'バナナ', 'カキ'),
 ('ミカン', 'バナナ', 'カキ')]

pythonのバージョンが3.8以上mathモジュールでも順列の個数を計算することができます。

mathモジュールによる組み合わせの個数の計算

import math
math.perm(5,3)

scipyモジュールによる組み合わせの個数の計算

from scipy.special import perm
comb(5,3)

10.0

組み合わせの公式

rが増える場合

組み合わせの計算で、nやrを増減させた場合の定理を考えます。

まず、組み合わせの公式に対して、rを1増やした場合の計算を考えます。公式を見れば次の公式が考えられます。

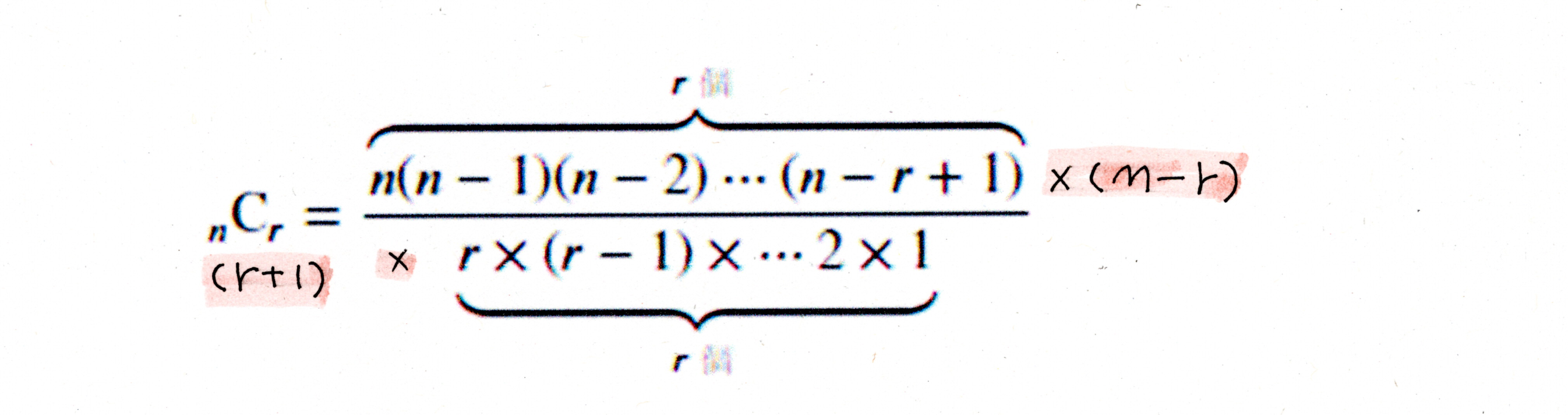
${}_n\mathrm{C}_r$でもう一人選べたらn-r人から1人選べるので順列がn-r倍になる。しかし、選ばれる人がr+1人と1人増えるので重複する順列がr+1倍になってしまうのでr+1で割る必要がある。

$\displaystyle{}_n\mathrm{C}_{r+1}=\frac{n-r}{r+1}{}_n\mathrm{C}_r$

また、${}_n\mathrm{C}_{r-1}$との関係を見る場合、rにr-1を代入して次の通りになります。

$\displaystyle{}_n\mathrm{C}_r=\frac{n-(r-1)}{(r-1)+1}{}_n\mathrm{C}_{r-1}= \frac{n-r+1}{r}{}_n\mathrm{C}_{r-1}$

nが増える場合

公式をしげしげとみればわかります。

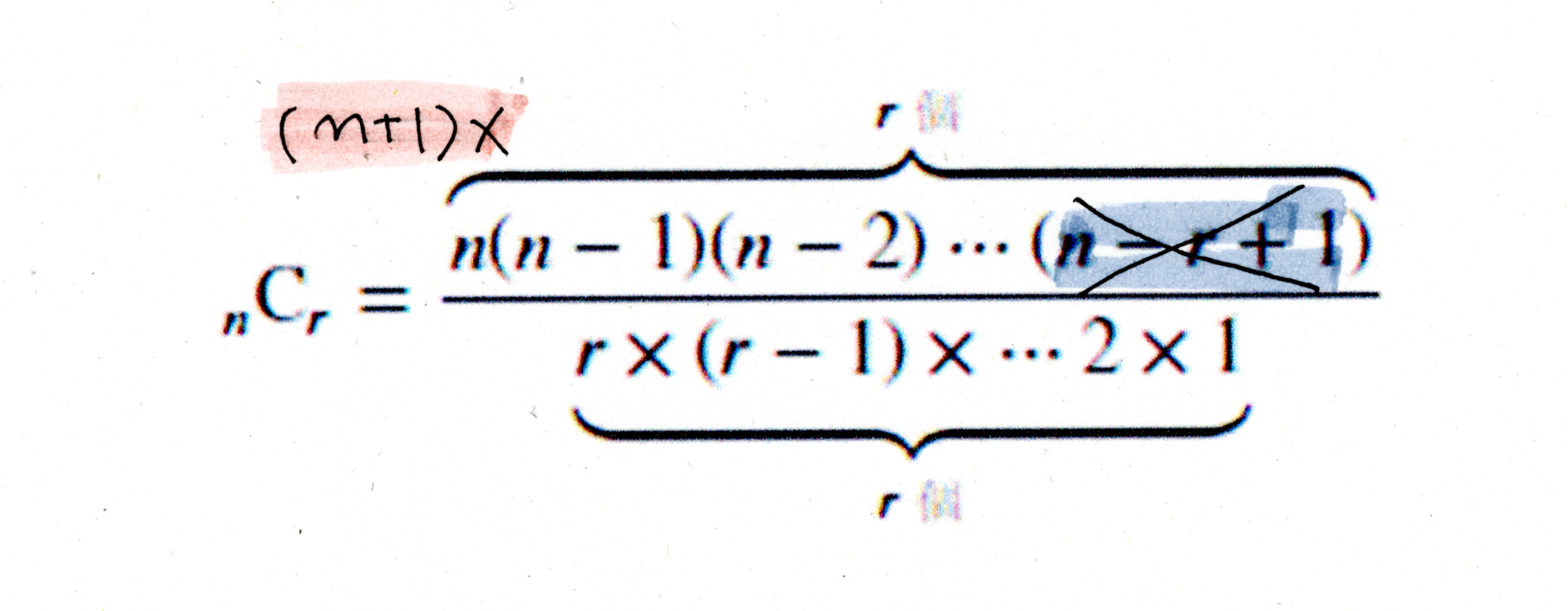
$_n\mathrm{C}_r$に比べ、新しく増えた1人が選ばれない組み合わせは$_n\mathrm{C}_r$と同じ、新しく増えた1人が選ばれた場合$_n\mathrm{C}_r$のうちのr人の1人がはじかれてしまうので、組み合わせは $\frac{r}{n-r+1}$倍になります。このため、

$\displaystyle{}_{n+1}\mathrm{C}_r=\left(1+\frac{r}{n-r+1}\right){}_n\mathrm{C}_r= \frac{n+1}{n-r+1}{}_n\mathrm{C}_r$となります。さらにnにn-1を代入すると次の通りになります。

$ \displaystyle \ _n C_r = \frac{n}{n-r} \ _{n-1}C_r$

#nもrもiずつ増える場合

やはり式を見れば

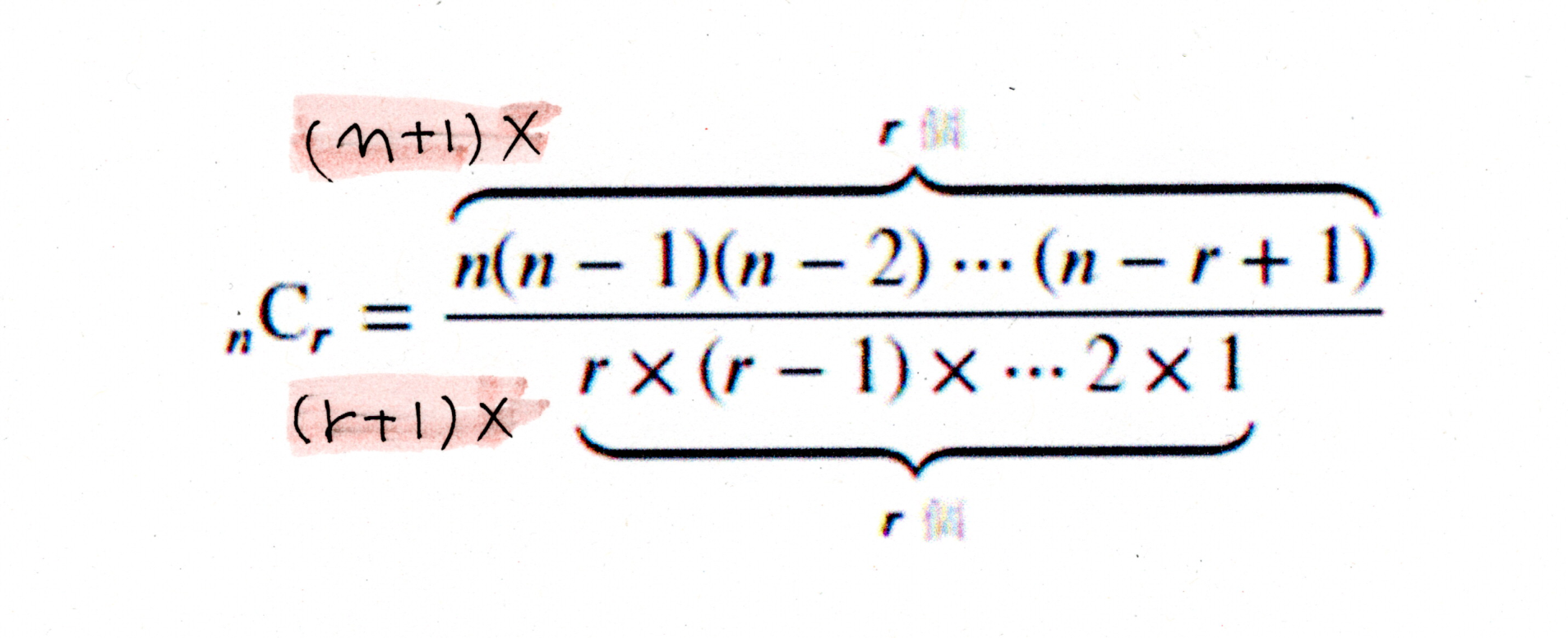
${}_{n+1}\mathrm{C}_{r+1}=\displaystyle\frac{n+1}{r+1} \ _n\mathrm{C}_r$

nにn-1、rにr-1を代入すると次の通りシンプルな式になります。

${}_{n}\mathrm{C}_{r}=\displaystyle\frac{n}{r} \ _{n-1}\mathrm{C}_{r-1}$

n人からr人を選んで、選ばれたr人から代表を決めることと、n人の中から代表を選び、代表以外のメンバーとして残ったn-1人からr-1人を選ぶことは同じです。

$r\;{}_n\mathrm{C}_r=n\;{}_{n-1}\mathrm{C}_{r-1}$

こんな素敵な導き方もあります。

期待値の計算に重宝する式

${}_{n+1}\mathrm{C}_{r+1}$において、背番号1からn+1からr+1人選ぶことを考えます。選ばれた中で背番号が一番大きい人で分類し、その中で残りのr人を選ぶと

$n+1\longrightarrow {}_{n}\mathrm{C}_{r}$

$n\longrightarrow {}_{n-1}\mathrm{C}_{r}$

$n-1\longrightarrow {}_{n-2}\mathrm{C}_{r}$

$r+1\longrightarrow {}_{r}\mathrm{C}_{r}$

ここから次の式を導くことができます。

$\sum\limits_{k=r}^{n}{}_k\mathrm{C}_r={}_{n+1}\mathrm{C}_{r+1}$

数学的には次の通り証明することができます。

${}_{k+1} \mathrm{C}_{r+1}={ }_k \mathrm{C}_{r+1}+{ }_k \mathrm{C}_r$

$\therefore \quad{ }_k \mathrm{C}_r={ }_{k+1} \mathrm{C}_{r+1}-{ }_k \mathrm{C}_{r+1}$

$\sum\limits_{k=r}^{n}{}_k\mathrm{C}_r=\sum\limits_{k=r}^n{ }_{k+1} \mathrm{C}_{r+1}-\sum\limits_{k=r}^n{ }_k \mathrm{C}_{r+1}$

$=\sum\limits_{k=r+1}^{n+1}{ }_k \mathrm{C}_{r+1}-\sum\limits_{k=r}^n{ }_k \mathrm{C}_{r+1}$

$={ }_{n+1} \mathrm{C}_{r+1}-{ }_{r} \mathrm{C}_{r+1}$

$={ }_{n+1} \mathrm{C}_{r+1}$

ただしここで$n\lt r:→{}_k\mathrm{C}_r=0$という条件が必要です。