重複順列、順列（N:ラベルあり K:ラベルあり）

重複順列、順列について、写像とPythonを使って整理します。制約なしの重複順列、単射の順列は最も基本的な位置づけとなりますが、全射の条件となると複雑な計算をする必要があります。この考え方は包除原理といいとても奥深いものがあります。

全射でも単射でもない制約なしの重複順列

重複順列（product sequence with repetition）について理解するため、次の問題を考えます。

問題1

5人の学生が合宿で2つの部屋に分かれて泊まることとします。各学生は、どちらの部屋でも自由に選ぶことができます。5人の学生は出席番号で表し、N={0, 1, 2, 3, 4}とします。また、部屋名はK={A, B}としたとき、部屋割りとして考えられる重複順列の一覧を生成し、その個数を計算してください。

重複順列の考え方

写像からみた重複順列

重複順列など場合の数では、慣習的に定義域を集合N、終域を集合Kとして、集合Nから集合Kへの写像として捉えます。図表1の１は、$A =\{0, 1\}$、$B=\{2, 4\}$となり、２は全員がAに泊まり$A=\{0, 1, 2, 3, 4\}$、Bには誰も泊まらず、$B=\emptyset$であることを示しています。

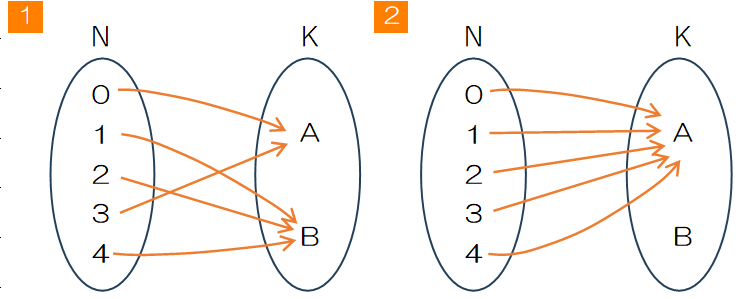
ここで次のものは写像になりせん。

集合Nの要素に対して対応する集合Kの要素がない、つまり野宿はできないということです。
集合Nの要素に対して集合K中に対応する要素が複数あることは許されません。つまり部屋Aで騒いで部屋Bで寝るということはできません。

一方、写像について全射や単射の制約なしの場合、次のものは問題ありません。

1つの集合Kの要素に対して複数の集合Nが対応すること、つまり相部屋OKということです。ここでは集合Kの要素Aは集合Nの0,1,3に対応しており単射ではないことがわかります。
集合Kの要素の中に対応する要素がないこと、つまり空き部屋OKということです。このことから、全射でないものも許されます。

上記のことから、重複順列は制約なし（unrestricted）の写像ということができます。

重複順列の生成と個数の計算

重複順列の生成手順を図にすると次のようになります。

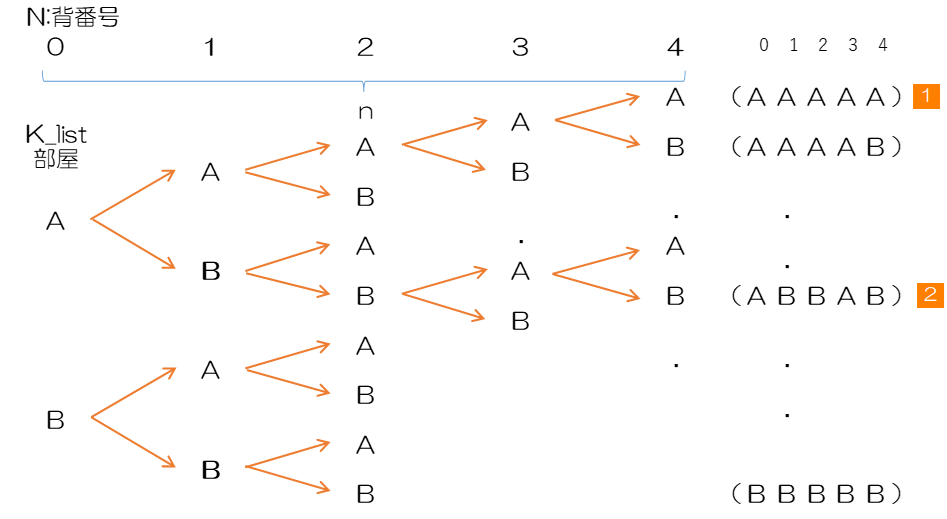
0がA,Bの2通りの部屋を選ぶことができ、その各々に対して1が2通り、さらにその各々について2が$2\times2=2^2=4$通り、・・・というように4までの5人に繰り返すので、$2^5=32 $通りとなります。最終的には、図の右側のように５人がどの部屋に泊まるかをタプルとして生成し、32個のタプルを1つのリストとしてまとめます。このように、重複順列の個数はkをn乗ずることにより求めることができるので、Pythonの標準モジュールには関数は用意されていません。この計算式は"k to the n-th power"と読み$\prod$はproductの略号です。

重複順列の個数

$_k\prod{_n}=k^n$

Pythonによる重複順列の生成と個数の計算

itertoolsモジュールのproduct関数による重複順列の生成

Pythonではitertoolsモジュールのproduct関数を使うと重複順列を出力することができます。itertoolsモジュールはPythonのFunction Programming Moduleに分類されており、イテレータといわれるデータを1つずつ順番に取り出す仕組みを生成する機能が盛り込まれています。Pythonの標準ライブラリの1つなので、Pythonがインストールされていれば使うことができます。ただし、ビルドイン関数ではないので、使用する都度、インポートする必要があります。

product関数で重複順列を生成するときは、集合の要素と、nの個数をrepeat=nの形式で引数を渡します。

戻り値として0,1,・・・が選んだ部屋AかBかを表すイテレータが生成されます。また、リストはpprint関数を使うと見やすく表示することができるので、あらかじめpprintをインポートしておきます。

itertoolsモジュールによる重複順列のリストの生成

import itertools
import pprint
k_list = ['A', 'B']
itertools_product_list = list(itertools.product(k_list, repeat = 5))
print('itertools product(2, 5) =',len(itertools_product_list))
pprint.pprint(itertools_product_list)

itertools product(2, 5) = 32
[('A', 'A', 'A', 'A', 'A'),
 ('A', 'A', 'A', 'A', 'B'),
（中略）
 ('A', 'B', 'B', 'A', 'A'),
 ('A', 'B’, 'B', 'A', 'B'),
（中略）
('B', 'B', 'B', 'B', 'A'),
('B', 'B', 'B', 'B', 'B')]

4.　イテレータをリストとして扱うときにはlist関数を使いリスト型に変換する必要があります。

6.　生成した重複順列は、pprint関数で出力すると行ごとに表示され見易くなります。

product関数は、直積、（デカルト積cartesian product）を生成する関数で、2つ以上の集合の要素間で総当たりの組み合わせを生成することができます。ここではk_listを集合と考え、このk_listを別の集合として5つ並べて直積を取るものと考え、repeat=5としています。その意味ではproduct関数の特殊な使い方捉えることもできます。

重複順列を生成する関数

重複順列を生成する関数の流れ

図表2のような重複順列を配列arrayに作成する場合、次の2つの考え方があります。

① n回forループを回し、arrayに各人がどの部屋を選ぶかを順次、追加

初期の定義時: array = [(, )]

1回目のループ: array = [(A, ), (B, )]

2回目のループ: array = [(A, A), (A, B), (B, A), (B, B)]

3回目のループ: array = [(A, A, A), (A, A, B), (A, B, A), (A, B, B) , (B, A, A), (B, A, B), (B, B,A), (B, B,B)]

・・

のように追加します。少し専門的になりますが、このような方法を幅優先探索（BFS = Breadth-First Search）といいます。

② はじめに1つ配列を作成し、そこから要素を入れ替え

1つ目　(A, A, A, A, A)

2つ目　(A, A, A, A, B)

3つ目　(A, A, A, B, A)

・・のように追加します。このような方法を深さ優先探索（DFS = Depth-First Search）といいます。

ここでは、流れがシンプルな①の幅優先探索でプログラムを作成します。重複順列を生成する流れは図表3のとおりです。

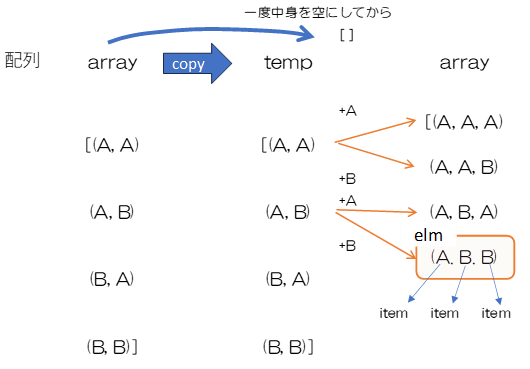
arrayの中の作成途中の重複順列をelmとして順次読み込み、itemは各人がどの部屋に入るかを表します。1つのelmに対しAを追加したものとBを追加したものというように複数個のタプルをarrayに追加します。この流れでは配列arrayを読み込みながら、そのarrayに重複順列を追加するという処理が必要になり、永久ループに陥る恐れがあります。そこで図表3のように、arrayの内容を1度リストtempにコピーし、arrayをクリアしたのちtempから順次読み込み、Aを使加えた重複順列と、Bを付け加えたタプルをarrayに追加していきます。

重複組み合わせを生成する関数

前節の考え方に沿って、重複順列を生成するPythonの関数を作成します。関数名は制約なし(unrestricted)の順列(permutation)という意味でperm_unrestricted_funcとし、itertoolsと同様にk_listとnの2つの引数として渡します。なお、重複順列の各重複順列は、タプルにします。タプルはリストとは異なり、1度作ると変更することができません。このような性質をイミュータブル（変更不可）といい、ミュータブル（変更可能）であるリストよりも構造が単純であるため、マシンへの負荷が少なることが期待できます。また、イミュータブルであることは不便な気もしますが、作成した配列を使っていろいろな処理をする場合、途中で勝手に変えられないので、予測不能なエラーが発生するリスクが少なくなるというメリットもあります。

重複組み合わせを生成する関数

引　数

k_list

集合Kの要素をタプルで指定

集合Nの要素の個数を指定

返り値

perm_unrestricted_list

重複順列を2重リスト形式で返す。

引　数

k_list

集合Kの要素をタプルで指定

引　数

集合Nの要素の個数を指定

返り値

perm_unrestricted_list

重複順列を2重リスト形式で返します。

def perm_unrestricted_func(k_list, n):
array = [()]
for _ in range(n):
temp = array
array = []
for elm in temp:
for item in k_list:
array.append(elm + (item,))
return array
n = 5
k_list= ['A', 'B']
perm_unrestricted_list = perm_unrestricted_func(k_list, n)
print('perm_unrestricted_func(2, 5) =',len(perm_unrestricted_list))
if perm_unrestricted_list == itertools_product_list:
print('perm_unrestricted_list == itertools_product_list')

perm_unrestricted_func(2, 5) = 32
perm_unrestricted_list == itertools_product_list

2.　arrayを初期化する際に、空のタプルを要素として持つリストとして定義します。次の4.でtempにコピーし6.で制作途中の重複順列を読み込む際に何かしらのタプルがないとエラーになるためです。

3.　定義域の数だけ4.～8.の処理をn回繰り返します。

1回目のループ: temp = [()], array = [(A ,), (B, )]

2回目のループ: temp = [(A,), (B,)], array = [(A, A), (A, B), (B, A), (B, B)]

3回目のループ: temp =[(A, A), (A, B), (B, A), (B, B)], array = [(A, A, A), (A, A, B), (A, B, A),・・のように推移します。

8.　リストtempからこれまで作成した1つ1つをelmとして取り出し、k_listの要素をitemとして取り出したitemを右側にitemを結合して新しいタプルとし、arrayに追加します。要素が1つだけのタプルは(item,)のように要素にカンマを付けます。

このことにより、arrayが、k_listからなる長さnの順列のリストを戻り値として返します。最終的にproduct関数と同じ結果になります。

単射としての順列

場合の数の中で最もよく使われる順列(permutation)を写像の視点から見るために、次の問題を考えます。

問題2

3人の学生が合宿でそれぞれ個室に泊まることとします。宿舎にはK={A, B, C, D, E}の5部屋が用意されており、学生は出席番号で表し、N={0, 1, 2}としたときの部屋割りとして考えられる順列を一覧にし、その場合の数を計算してください。

順列についても、Pythonに用意されている関数を使い個数を求め生成するとともに、関数を作成し結果を比較します。

写像からみた順列と個数の計算

写像から見た順列の考え方

こんな時代なのでみんな個室がよい、ということで誰もが同じ部屋に泊まらないような部屋割りも考えられます。写像の視点で見ると、終域に属する要素はすべてその定義域の要素にただ一つだけ対応させる単射(injective)となります。図にすると次の通りです。

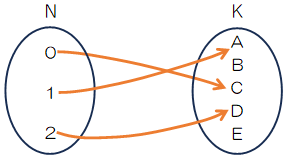
SciPyライブラリ、mathモジュールのperm関数による順列の場合の数の計算

SciPyライブラリのspecial サブモジュールにあるperm関数により順列の場合の数を計算することができます。このほか新しいバージョンではmathモジュールにもperm関数が追加されました。なお、組み合わせについては次章で扱いますが、ここでも必要になるのでcomb関数もご紹介しておきます。

math関数、SciPyライブラリを使い順列の個数を計算する

from scipy.special import perm, comb
import math
print(f'scipy.special.perm(2, 5) = {perm(n, len(k_list), exact = True)}')
print(f'scipy.special.comb(2, 5) = {comb(n, len(k_list), exact = True)}')
print(f'math.perm(2, 5) = {math.perm(n, len(k_list))}')
print(f'math.comb(2, 5) = {math.comb(n, len(k_list))}')

scipy.special.perm(2, 5) = 20
scipy.special.comb(2, 5) = 10
math.perm(2, 5) = 20
math.comb(2, 5) = 10

1.　perm関数、comb関数はSciPyライブラリのscipy.specialモジュールからインポートします。

2.　mathモジュールはモジュール全体をimportするのが一般的です。

3.　SciPyライブラリのperm関数は組み合わせの数を小数点で返します。整数で戻り値を返すときは、exact = Trueを指定します。

4.　同様に、SciPyライブラリのcomb関数により組み合わせの個数を計算します。

5.　mathモジュールのperm関数は返り値として整数で組み合わせの数を返します。同様に6.においてcom関数で組み合わせの個数を計算します。ただし、Pythonのバージョン3.8以降でないと使うことはできません。

順列、組み合わせおよび階乗を計算する関数を作成する

通常、順列はn個からr個を重複なく選ぶと考え$\ _n P_r$と表記しますが、写像では$\ _k P_n$とするのが一般的です。

順列の個数の計算

$\displaystyle \ _n P_r = \frac{n!}{(n-r)!}=\;\overbrace {n(n-1)(n-2)・・・(n-r+1) \quad}^{r個}$

$\displaystyle \ _n C_r =\frac{\ _n P_r}{n!}=\frac{n!}{r!(n-r)!} = \frac{\overbrace {n(n-1)(n-2)\cdots (n-r+1)}^{r個}}{\underbrace {r\times (r-1)\times \cdots 2 \times 1}_{r個}}$

$\displaystyle \ _k C_n =\frac{\ _k P_n}{n!}=\frac{k!}{n!(k-n)!} = \frac{\overbrace {k(k-1)(k-2)\cdots (k-n+1)}^{n個}}{\underbrace {n\times (n-1)\times \cdots 2 \times 1}_{n個}}$

$\displaystyle \ _k P_n = \frac{k!}{(k-n)!}=\;\overbrace {k(k-1)(k-2)・・・(k-n+1) \quad}^{n個}$

$\displaystyle \ _k C_n =\frac{\ _k P_n}{n!}=\frac{k!}{n!(k-n)!} = \frac{\overbrace {k(k-1)(k-2)\cdots (k-n+1)}^{n個}}{\underbrace {n\times (n-1)\times \cdots 2 \times 1}_{n個}}$

順列、組み合わせの個数を計算する関数を作成しますが、これらの計算では階乗の計算が必要になります。そこで、階乗を計算するfactorial関数を作成し、factorial関数を使って順列を計算するP関数、組み合わせを計算するC関数を作成します。これらの関数はよく使われるので、英字1文字にします。

①階乗：factorial 関数

引数を正の整数nとして、nから1までを掛け合わせます。ただし$ _ 5 P_3=5\times 4\times 3$のような計算をする場合には途中で止めても構いません。そこで、2つ目のrという引数を追加し、デフォルトをNoneとしておきます。階乗は0!=1となることが必要です。

②順列：P関数

引数として集合Kの個数kと集合Nの個数nを指定します。つまりk個から選んで並べる順列の個数を計算します。P関数は$k \lt p$の場合は0、$n=0$の場合は1となることが必要です。

③：C関数

P関数と同様に組み合わせの個数を計算します。C関数は$k \lt n$の場合は0、$n=0$の場合は1となることが必要です。

階乗、順列、組合せを計算する関数

def factorial(n, r=None):
if r is None:
r = n
result = 1
for i in range(n, n-r, -1):
result *= i
return result
def P(k, n):
if k < n:
return 0
return factorial(k, n)
def C(k, n):
if k < n:
return 0
return factorial(k, n) // factorial(n)
print(f'0!={factorial(0)} 1!={factorial(1)} 5!={factorial(5)} 5X4X3={factorial(5,3)}')
print(f'5P5={P(5,5)} 5P3={P(5,3)} 5P1={P(5,1)} 5P0={P(5,0)} 5P6={P(5,6)}')
print(f'5C5={C(5,5)} 5C3={C(5,3)} 5C1={C(5,1)} 5C0={C(5,0)} 5C6={C(5,6)}')

0!=1  1!=1  5!=120  5X4X3=60
5P5=120  5P3=60  5P1=5  5P0=1  5P6=0
5C5=1  5C3=10  5C1=5  5C0=1  5C6=0

1.　2番目の仮引数r=Noneと指定することでrを指定しない場合は初期値でNone、指定した場合はその値がrに代入されます。

2.　1.を受けてrがNoneであれば3.でnをrに代入されます。このことにより、n!の計算ができるようになります。

5.　階乗の計算式は$n\times(n-1)\times(n-2)\times\cdots(n-r+1)$です。この計算を実現するためfor i in range(n, n -r, -1)とします。3つ目の引数が-1の場合、降順にiを回しますが2番目の引数は1つ先まで指定するので、n-rとするとn-r+1で止まります。

9.　順列は基本的にはfactorial関数を適用しますがk < nの場合は0になるように明記します。

k,n,rが正の整数であれば、階乗、順列、組合せの計算が正しくできることがわかりました。

itertoolsモジュールのpermutations関数による順列の生成

Pythonの標準モジュールであるitertoolsモジュールのpermutations関数により、順列を生成することができます。引数は重複順列と同様です。

itertoolsモジュールによる順列のリストの作成

k_list = ['A', 'B', 'C', 'D', 'E']
n = 3
itertools_perm_list = list(itertools.permutations(k_list,n))
print('itertools.permutations(5, 3) = ',len(itertools_perm_list ))
pprint.pprint(itertools_perm_list)

itertools.permutations(5, 3) =  60
[('A', 'B', 'C'),
 ('A', 'B', 'D'),
 （中略）
('E', 'D', 'A'),
 ('E', 'D', 'B'),
 ('E', 'D', 'C')]

2.　itertoolsモジュールのpermutations関数により、順列のリストを出力することができます。

順列の個数は$5\times4\times3=60$となります。

順列を生成する関数を作成

順列を生成する関数を自作します。順列は単射になるのでperm_injective_funcという関数名にします。重複順列を生成するperm_unrestricted_func関数とほぼ同じ流れになりますが、単射にするため、itemをelmに結合する時点で先客がいる場合、候補から外れるのでarrayに追加しないようにします。

順列を生成する関数

引　数

k_list

集合Kの要素をタプルで指定

集合Nの要素の個数を指定

返り値

perm_unrestricted_list

順列を2重リスト形式で返す。

引　数

k_list

集合Kの要素をタプルで指定

引　数

集合Nの要素の個数を指定

返り値

perm_injective_list

順列を2重リスト形式で返します。

def perm_injective_func(k_list, n):
array = [()]
for cnt in range(n):
temp = array
array = []
for elm in temp:
for item in k_list:
if item not in elm:
array.append(elm + (item,))
return array
k_list = ['A', 'B', 'C', 'D', 'E']
n = 3
perm_injective_list = perm_injective_func(k_list, n)
print('unrestricted count = ',len(k_list)**n,'perm_injective_func(3, 5) = ',len(perm_injective_list))
if perm_injective_list == itertools_perm_list:
print('perm_injective_list == itertools_perm_list')

unrestricted count =  125 perm_injective_func(3, 5) =  60
perm_injective_list == itertools_perm_list

8.　if item not in elmの条件文で、入ろうとした部屋に誰かが入っていないかを判断します。

9.　8.により単射の要件を満たす可能性のある場合に限り、elmにitemを結合しarrayに追加します。

perm_injective_func関数では、学生1人1人についてリストに追加するときに単射の判断をしていますが、最後の1人のところで判断する方法も考えられます。この場合、8行目の判断の回数が少なくてすむ代わりに、終了直前までarrayに単射の要件を満たさないタプルも候補として残しておく必要があるので、どちらの効率が良いか一概には言えません。

集合Kに重複する要素がある場合の順列

itertoolsのpermutations関数と#6のperm_injective_func関数を使い、k_list = ['A', 'A', 'A', 'B', 'B']のように要素が重複させた場合の順列を生成します。

重複のある要素から順列を生成する

k_list = ['A', 'A', 'A', 'B', 'B']
n = 3
itertools_perm_dup_list = list(itertools.permutations(k_list,n))
perm_injective_dup_list = perm_injective_func(k_list, n)
print('itertools.permutations(3, 5) with duplication = ',len(itertools_perm_dup_list))
print('perm_injective_func(3, 5) with duplication = ',len(perm_injective_dup_list))

itertools.permutations(3, 5) with duplication =  60
perm_injective_func(3, 5) with duplication =  0

3.　itertoolsのpermutationsの結果は、perm_injective_dup_listというリストに代入します。dupはduplicateの略です。

4.　同様にperm_injective_funcの結果はリストperm_injective_dup_listに代入します。

itertoolsの場合は問題なく順列を生成しましたが、perm_injective_func関数は0件（空のリスト）になってしまいます。同じ要素があると順列の候補から外してしまうので当然の結果です。

このようなケースはそう多くはありませんが、次のような問題を解く場合、重複する要素の順列を作成できると非常にありがたいです。

多項定理による順列

問題

青いボールが3個、赤いボールが2個、緑色のボールが2個あります。これらの7個上ボールを一列に並べると、その並べ方は何通りになりますか。ただし、青、赤、緑のボールはそれぞれ区別しないものとします。

意外と難しい問題です。多項定理（multinomial theorem）が何かはさておいて、ここでの問題に絞って計算します。

7個のボールをいったんすべて区別があるとして順列で並べます。例えば青の3個を青1、青２、青３のようにラベルを付ければ、7!通りになります。ところが、青の３つは区別しない前提なので3!個は同じ順列として扱います。

同じように赤、緑が2個なので2!で割り返すことで計算することができます。

$n=p_1 + p_2 + p_3 + \cdots + p_k$

$\displaystyle \frac{n!}{p_1! \cdot p_2! + \cdot p_3! + \cdots + p_k!}$

この考え方によると、重複する要素がある順列を生成して、同じ順列がある場合は1つにまとめることで多項定理の計算をすることができます。関数名は順列から多項展開するのでmultinomial_by_perm_funcとし、k_listには色が、n_listにはそれぞれの個数を入れて引数として渡します。順列は、以前作成したperm_injective_funcを使いますが、この関数はk_listに同じ文字列があるとうまく動かないので、いったん数字で順番を生成し、この順番に番号を指定して要素を取り出します。ここで作成したリストから新しいリストを作成しますが、すでに新しいリストにある組み合わせは追加しないようにすることで重複をなくすようにします。

重複する要素に対応する順列を生成する

def perm_injective_dup_func(k_list, n):
perm_seq = []
for elm in perm_injective_func(range(len(k_list)),n):
perm_seq.append(tuple([k_list[i] for i in elm]))
return perm_seq
k_list = ['A', 'A', 'A', 'B', 'B']
n = 3
perm_injective_dup_list = perm_injective_dup_func(k_list, n)
print('unrestricted count = ',len(k_list)**n,'perm_injective_dup_func(3, 5) = ',len(perm_injective_list))
if perm_injective_dup_list == itertools_perm_dup_list:
print('perm_injective_dup_list == itertools_perm_dup_list')

unrestricted count =  125 perm_injective_dup_func(3, 5) =  60
perm_injective_dup_list == itertools_perm_dup_list

3.　 perm_injective_func関数を実行するときに、引数k=listを集合Kの要素ではなく、要素の個数の大きさの(range(len(k_list)),n)とします。このことにより、k_listに重複した要素があっても、要素の順番で順列を生成することができます。

5.　最終的には、k_listでの順番から実際の値に変換する必要があるので(k_list[item]としてリストを作り直します。

このように、itertoolsと同じように重複のある順列を生成することができました。つぎにいよいよ多項定理による順列を生成する関数を作成します。引数としては辞書形式で渡して、これをいったんリストに変換したのち、重複のある順列を生成しarrayに追加しますが、ここから同じ並びのものははじくようにします。この際に順列を生成するときに同じ要素があったら追加しない、というような手順を使います。

重複要素を含む順列を生成する

def multinomial_by_perm_func(dict):
k_list=[]
for key, value in dict.items():
k_list.extend([key] * value)
array=[]
for elm in perm_injective_dup_func(k_list, len(k_list)):
if elm not in array:
array.append(elm)
return array
dict = {'青':2, '赤':3, '緑':2}
multinomial_by_perm_list = multinomial_by_perm_func(dict)
len(multinomial_by_perm_list)
return array

[('青', '青', '青', '赤', '赤', '緑', '緑'),
 ('青', '青', '青', '赤', '緑', '赤', '緑'),
 ('青', '青', '青', '赤', '緑', '緑', '赤'),
 ('青', '青', '青', '緑', '赤', '赤', '緑'),
 ('青', '青', '青', '緑', '赤', '緑', '赤'),
 ('青', '青', '青', '緑', '緑', '赤', '赤'),
 ('青', '青', '赤', '青', '赤', '緑', '緑'),

2.　順列を生成するためk_list=["青","赤","緑"]、n_list=[3, 2, 2]ならば、elements=[‘青’, ‘青’, ‘青’,’赤”, ’赤”,”緑”, ”緑”]となるようなリストを作成します。[k] * n for kとなっているので[[‘青’, ‘青’, ‘青’],[’赤”, ’赤”],[”緑”, ”緑”]]のように色ごとにリストが分かれてしますので、sum関数にリストと[]を適用することで余計なかっこを外します。

4.　 perm_injective_funcでは、単射の条件を適用するため、同じ要素を選ぶことができません。そこで、いったんの0からボールの個数-1までのn個について、リストを作成したのちた順列を生成し、番号を色の記号に戻します。

8.　 perm_injective_funcで作成したperm_injective_listに対し、同じ組み合わせの要素があったときは、新しいリストarrayに追加しないようにします。

重複組み合わせを全射にする

全射の考え方と生成するプログラム

写像からみる全射の考え方

ここからが山場です。全射の考え方を理解するため次の問題を考えてみましょう。

問題3

5人の学生が合宿で2つの部屋に分かれて泊まることとします。各学生は、どの部屋を自由に選んでよいものとしますが、空き部屋が出ることは許されません。5人の学生は出席番号で表し、N={0, 1, 2, 3, 4}とします。また、部屋名はK={“A”, ”B”}としたとき、部屋割りとして考えられる重複順列を生成し、場合の数を計算してください。

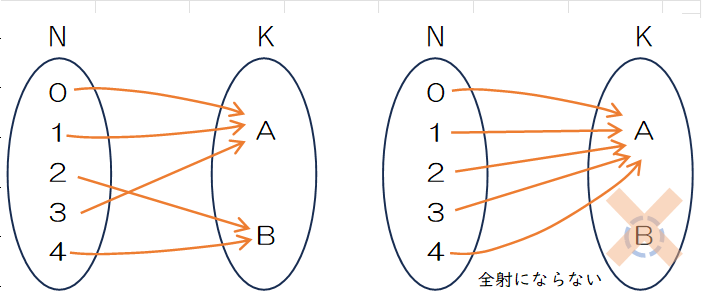
#2では全学生が部屋A、または部屋Bに集中している重複順列が見られます。宿の方がせっかく2部屋を確保してくれたのに空き部屋にしてしまうのでは、品格を疑われてしまいます。そこで、少なくとも1部屋に1人は泊まるような重複順列を考えます。集合Kに集合Nから対応つけられない要素が存在することを許さないのが全射(surjective)このため、図表5の左のような(A, A, B, A, B)は問題ありませんが、右のように(A, A, A, A, A)や、図にはありませんが、(B, B, B , B, B)のような重複順列は対象になりません。

全射の重複順列を生成する関数

Pythonの標準ライブラリには、全射の重複順列の生成や個数の計算をする関数が見当たらないので自作します。重複組み合わせの全射という意味で関数名をperm_surjective_funcとします。引数は重複順列を生成する関数と同じです。全射の条件を満たしているかは最後の1人にならないと判断できないので、itemをelmに追加するところをn-1とそれ以前に分けて、最後の1人で全射かどうかを判断します。

重複順列を配列として出力

def perm_surjective_func(k_list, n):
array = [()]
for cnt in range(n):
temp = array
array = []
for elm in temp:
for item in k_list:
if cnt < n-1:
array.append(elm + (item,))
else:
if set(k_list).issubset(set(new_elm := elm + (item,))) :
array.append(new_elm)
return array
n = 5
k_list= ['A', 'B']
perm_surjective_list = perm_surjective_func(k_list, n)
print('unrestricted = ',len(k_list)**n,'surjective = ',len(perm_surjective_list))
pprint.pprint(perm_surjective_list)

unrestricted =  32 surjective =  30
[('A', 'A', 'A', 'A', 'B'),
 ('A', 'A', 'A', 'B', 'A'),
 ('A', 'A', 'A', 'B', 'B'),
 ('A', 'A', 'B', 'A', 'A'),
 （中略）
('B', 'B', 'B', 'A', 'B'),
 ('B', 'B', 'B', 'B', 'A')]

8.　n=4の場合、0 から3人目の2までについては、無条件にnew_elmをarrayに追加します。このため、n<1が条件になります。

11. 最後の1人は9.にあてはまらないので、12.で作成した重複順列が全射の要件を満たすnew_elmのみを要素をarrayに追加します。なおnew_elm := elm + (item,)は、new_elmにelm + (item,)を代入したうえで、この中にk_listの要素が含まれているかを判断します。このような”:=”を:ウォルラス演算子（Walrus operator）といい、形からセイウチ演算子と呼ばれます。ただし、ウォルラス演算子はPythonのPythonの v3.8以降でないと使うことはできないので、その場合は次のようにコーディングします。

for elm in temp:

for item in k_list:

new_elm = elm + (item,)

if cnt < n-1:

array.append(new_elm)

else:

if set(k_list).issubset(new_elm):

array.append(new_elm)

全射の重複順列を集合(set)に変換すると{A, B}となり、k_listの個数と等しくなります。これに対して全射でない(A, A, A, A, A)は{A}となり、k_listの個数よりも小さくなります。このように、全射の判断をするために、作成した配列を集合に変換し、その個数と要素の種類を比較するのが定石です。この例では、制約なしの32通りに対し、(A, A, A, A, A)、(B, B, B, B, B)の2通りが取り除かれ、30通りが全射の場合の数であることがわかりました。

全射の重複順列を集合で考える

k=2のような簡単な例であれば、直ぐに計算することはできますが、kの数が増えるにしたがって話は複雑になります。そこで、集合の考え方を使って整理し、kがどんなに大きくなっても対応できるようにしたいと思います。

ここから、全射の重複順列の個数を計算します。ここでのコツはAが空室になる事象を集合A、Bが空室になる事象を集合B、というように空室になる事象を考えることです。

重複順列では、集合Kの要素Aが集合Nと対応付けられない重複順列を集合Aと定義します。この場合、(B, B, B, B, B)が当てはまります。一方(A, A, A, A, A)のように要素Bが集合Nと関連付けられない重複順列を集合Bと定義します。ここから、全射の条件を満たさない重複順列は$A \cup B$になり、2個になります。これに対して全ての重複順列は全体集合(universe)といい集合Uで表します。ここでは集合Uの要素数は32個になります。したがって求める全射の重複順列は集合Aでも集合Bでもないものを数えればよいことになります。これは$\overline{A\cup B})$のようになり、個数は全体集合Uの個数から$A\cup B$の個数を差し引いた30個になります。

2つの集合の演算

全射の計算をする前提として2つの集合演算の一般的な公式を具体例を使い整理します。まず、次の3つの集合を定義します。

全体集合Uとして1から20までの整数を定義します。

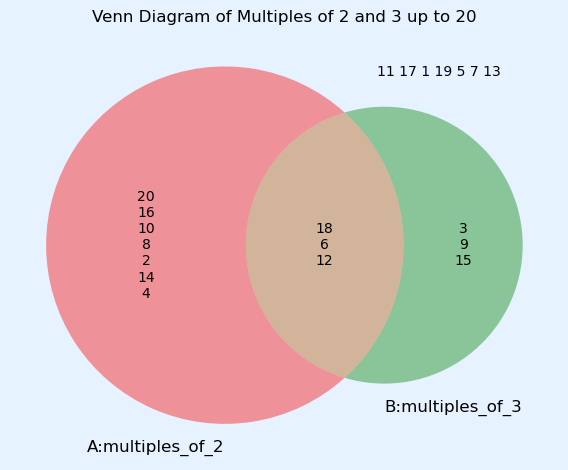
2の倍数：集合A={2, 4, 6, 8,10, 12, 14, 16, 18, 20}の10個

3の倍数の集合をB={3, 6, 9, 12, 15, 18}の6個

集合Aと集合Bの共通部分は積集合（intersection)といい、 $A \cap B=\{6, 12, 18\}$の3個になります。6の倍数なので簡単に求めることができます。また、集合Aには含まれるが集合Bに含まれない要素の集合を差集合（difference)といい$A-B=A\setminus B=A\cup \overline{B}=\{2, 4 , 8, 10, 14, 16, 20\}$の7個になります。同様に$B-A=B\setminus A=B\cup \overline{A}=\{3, 9, 15\}$の3個になります。ここまでは簡単ですが、集合Aか集合Bのいずれかに含まれている要素である和集合（union）$A \cup B=\{2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20\}$の13個、またAでもBでもない集合Uの補集合$\overline{A \cup B}=U\setminus (A \cup B)=\{1, 5, 7, 11, 13, 17, 19\}$の7個となりここまでくるとこれは数えるのには少し骨が折れます。

操作	英語	演算子	記号	内包的記法
和集合	union	\|	$A\cup B$	$\{x \mid x \in A \vee x \in B\}$
積集合	intersection	&	$A\cap B$	$\{x \mid x \in A \wedge x \in B\}$
差集合	difference	-	$A\cap B$	$\{x \mid x \in A \wedge x \notin B\}$
補集合	(complement )		$A \overline A$ $U \setminus A$	$\{x \mid x \in U \wedge x \notin A\}$

Pythonを使って集合演算を行う際、Pythonでは3列目の演算子を使うと、それぞれの集合演算をすることができます。

2つの集合の演算

n = 20
U = set(range(1, n + 1))
A = set(range(2, n + 1, 2))
B = set(range(3, n + 1, 3))
union = A | B
intersection = A & B
difference_AB = A - B
difference_BA = B - A
symmetric_difference = A ^ B
complement = (U - (A | B))
print(f'A | B = {union}')
print(f'A & B = {intersection}')
print(f'A - B = {difference_AB}')
print(f'B - A = {difference_BA}')
print(f'U - (A | B)= {complement}')

A | B = {2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20}
A & B = {18, 12, 6}
A - B = {2, 4, 8, 10, 14, 16, 20}
B - A = {9, 3, 15}
U - (A | B)= {1, 5, 7, 11, 13, 17, 19}

2.　整数を要素とする集合を定義するため、range関数で範囲を定めset関数で集合に変換します。

3.　集合Aは2の倍数2の倍数の集合を定義するため、range関数で(2,n+1,2)とすることにより、2から始まり2つおきに整数を設定することができます。

4.　同様に集合Bは3から始まり3つおきの整数としてset(range(3, n + 1, 3))と定義します。

5.　これ以降は、定義した集合に対して演算を行います。

2つの集合のベン図

これらの関係はベン図にするとわかりやすくなります。2集合のベン図はmatplotlibライブラリの拡張ライブラリであるvenn2で描くことができます。なお、venn2は使用する際、一度だけpip install matplotlib_vennによりインストールする必要があります。

２つの集合のベン図を描く

from matplotlib import pyplot as plt
from matplotlib_venn import venn2
fig,ax = plt.subplots()
diagram2 = venn2([ A , B], set_labels=('A:multiples_of_2', 'B:multiples_of_3'))
plt.title('Venn Diagram of Multiples of 2 and 3 up to 20')
diagram2.get_label_by_id('10').set_text('\n'.join(map(str,difference_AB)))
diagram2.get_label_by_id('01').set_text('\n'.join(map(str,difference_BA)))
diagram2.get_label_by_id('11').set_text('\n'.join(map(str,intersection)))
plt.text(0.6, 0.5, ' '.join(map(str,complement)), ha='right', va='top')
fig.patch.set_facecolor('#e6f2ff') #fig.patch.set_facecolor('#e6f2ff'):
plt.tight_layout()
plt.show()

2.　venn2はmatplotlibとは別にインポートする必要があります。

4.　venn2関数は2つの集合（AとB）を引数として受け取り、ベン図を描画します。set_labelsパラメータで各集合のラベルを指定しています。

6.　ベン図の各領域へのテキスト追加: get_label_by_idメソッドを使用して、ベン図の特定の領域にアクセスし、set_textで内容を設定しています。8行目までIDは以下のように対応します：

'10': Aのみの領域

'01': Bのみの領域

'11': AとBの共通部分テキストは'\n'.join(map(str,intersection))を使用して複数の要素を改行で区切って表示しています。

集合intersectionには積集合が整数で列挙されていますが、文字として表示するため、全て文字列に変換します

intersection（集合）の各要素を文字列に変換します。

str関数がintersectionの各要素に適用されます。

変換された文字列の要素を改行文字（\n）で結合します。

なお、集合（set）の場合、要素が昇順に並ぶとは限らないので注意が必要です。

和集合と補集合の個数の計算

ベン図を見ると、集合Aと集合Bの和集合の数は、集合Aと集合Bの個数から積集合を引いた数になることがわかります。なお、集合Aの要素の数をn(A)と定義します。

\begin{align*} n(\overline{A\cup B}) &= n(U) - n(A \cup B) && \text{補集合の性質} \\ &= n(U) - \{n(A) + n(B) - n(A \cap B)\} && \text{包除原理} \\ &= n(U) - \{n(A) + n(B)\} + n(A \cap B) && \text{括弧の展開} \end{align*}

集合演算で確認します。

和集合、和集合の補集合の要素の個数

print(f'n(A | B)={len(A|B)}')
print(f'n(A)+n(B)-n(A & B)={len(A)+len(B)-len(A&B)}')
print(f'n(U)-n(A & B)={len(U-(A|B))}')

n(A | B)=13
n(A)+n(B)-n(A & B)=13
n(U)-n(A & B)=7

1.　$n(A \cup B)$を計算すると13個となり正しく計算することができました。

2.　$n(A)+n(B)-n(A \cap B)=10+6-3=13$となり、1と一致することがわかります。

3.　全体集合の個数n(U)=20から、$n(A \cup B)$を差し引くと7となり正しく計算できたことがわかります。

例題への適用

集合で考えると、全事象Uは$2^5=32$通り、Aは(B, B, B, B, B)の$1^5=1$通り、Bも (A, A, A, A, A)も$1^5=1$通りになります。AもBも空室はありえないので、$n(A\cap B) =\varnothing$、となります。UからAとBを差し引き、32-1-1=30通りになります。集合演算では次のようになります。なお、一般に集合Aの個数はn(A)のように表現します。

n=5,k=2のときの全射の重複順列の個数

$n(U)=2^5=32$

$n(A)= n(B)=1^5$

$n(A\cap B)=0$

$n(A\cup B)=n(A) + n(B) - n(A\cap B) = 1 + 1 - 0=2$

$n(\overline{A\cup B})=n(U)-\{n(A)+n(B)-n(A\cap B)\}=30$

計算結果が合致しました。

部屋数k=3の場合

写像による計算

集合Kの要素が3つになると、話がむつかしくなります。例として、n={0, 1, 2, 3, 4}、k={A, B, C} としてリストを作成します。

図の左のような(A, A, C, A, C)のようにBが選ばれない重複順列はもとより右のように(A, A, A, A, A)は全射になりません。

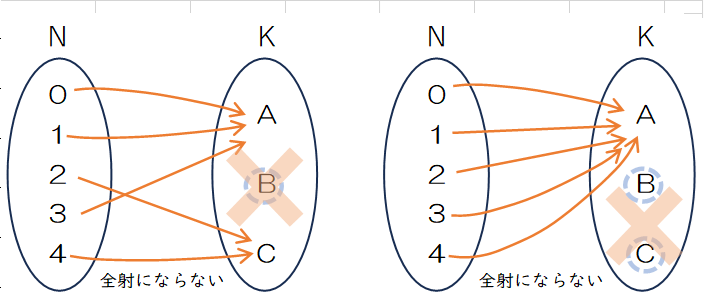
早速#6で作成したperm_surjective_func関数を使い、重複順列を生成したのち個数を数え、制約なしの重複縦列と比べます。

K=3の場合の全射の計算

n = 5
k_list= ['A', 'B', 'C']
perm_surjective_list = perm_surjective_func(k_list, n)
print('unrestricted = ',len(k_list)**n,'surjection = ',len(perm_surjective_list))
pprint.pprint(perm_surjective_list)

unrestricted =  243 surjection =  150
[('A', 'A', 'A', 'B', 'C'),
 ('A', 'A', 'A', 'C', 'B'),
 ('A', 'A', 'B', 'A', 'C'),
 ('A', 'A', 'B', 'B', 'C'),
 ('A', 'A', 'B', 'C', 'A'),
 ('A', 'A', 'B', 'C', 'B'),
（中略）
('C', 'C', 'C', 'C', 'C'),

2.　perm_surjective_func関数で計算した結果を、リストperm_surjective_listに代入します。

3.　重複順列$3^5=243$通りのうち、全射は150通りになります。この差の分析をして、個数の計算方法を考えます。

3つの集合の演算

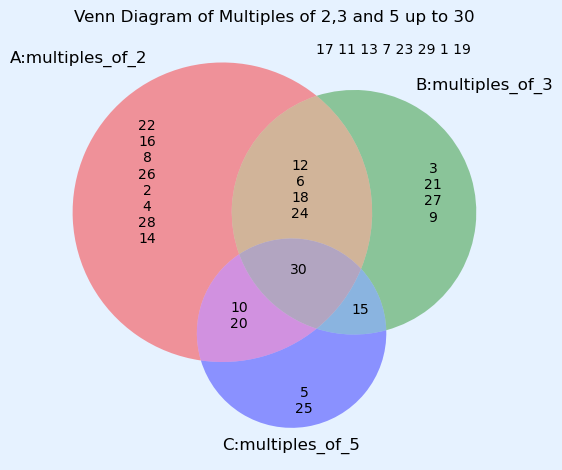
全体集合Uとして1から30までの整数を定義します。これに対して、

2の倍数の集合A={2, 4, 6, 8,10, 12, 14, 16, 18, 20, 22, 24,26,28,30}の10個、

3の倍数の集合をB={3, 6, 9, 12, 15, 18,21,24,27,30}の6個、

5の倍数の集合をB={5, 10, 15, 20, 25, 39}

とします。

集合A集合B集合Cの共通部分（intersection) $A \cap B=\{30\}$の1個になります。30の倍数なので簡単に求めることができます。

次に3つの集合の場合の複雑な例として集合A、集合Bの要素ではあるが集合Cの要素ではないような集合が考えられます。特にきまった名称はありませんが、ここではAとBの「積集合からCを除いた部分」と呼ぶことにします。このようなケースは次の3つが考えられます。

AとBの積集合からCを除いた部分　$A \cap B \cap \overline{C}=\{6, 12, 18, 12, 24\}$

AとCの積集合からBを除いた部分$A \cap C \cap \overline{B}=\{10, 20\}$

BとCの積集合からAを除いた部分$B \cap C \cap \overline{A}=\{15\}$

次に集合Aには含まれるが、その他の集合には含まれないような集合を相対的補集合(relative_complement)といいます。このような集合も次の3つのケースがあります。

$A \cap\overline{B}\cap\overline{C}=A \setminus B \setminus C={2, 4, 8, 14, 16, 22, 26, 28}$

$B \cap\overline{A}\cap\overline{C}=B \setminus A \setminus C={3, 9, 21, 27}$

$C \cap\overline{A}\cap\overline{B}=C \setminus A \setminus B={5, 25}$

1から30までの整数

n = 30
U = set(range(1, n + 1))
A = set(range(2, n + 1, 2))
B = set(range(3, n + 1, 3))
C = set(range(5, n + 1, 5))
union_ABC = A | B | C
intersection_ABC = A & B & C
intersection_AB_minus_C = A & B - C
intersection_BC_minus_A = B & C - A
intersection_AC_minus_B = A & C - B
difference_A_minus_BC = A - B - C
difference_B_minus_AC = B - A - C
difference_C_minus_AB = C - A - B
complement_ABC = (U - (A | B | C))
print(f'A | B | C ={union_ABC}')
print(f'A & B & C = {intersection_ABC}')
print(f'A & B - C = {intersection_AB_minus_C}')
print(f'B & C - A = {intersection_BC_minus_A}')
print(f'A & C - B = {intersection_AC_minus_B}')
print(f'A - (B | C) = {difference_A_minus_BC}')
print(f'B - (A | C) = {difference_B_minus_AC}')
print(f'C - (A | B) = {difference_C_minus_AB}')
print(f'U - (A | B | C) = {complement_ABC}')

A | B | C ={2, 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30}
A & B & C = {30}
A & B - C = {24, 18, 12, 6}
B & C - A = {15}
A & C - B = {10, 20}
A - (B | C) = {2, 4, 8, 14, 16, 22, 26, 28}
B - (A | C) = {27, 9, 3, 21}
C - (A | B) = {25, 5}
U - (A | B | C) = {1, 7, 11, 13, 17, 19, 23, 29}

2.　全体集合として1からn =30までの整数を集合Uとして定義します。定義するときはrangeで定義した範囲にset関数を適用します。同様に2から5で次の通り集合を定義します。

U: 1から30までのすべての整数

A: 2の倍数（2, 4, 6, ..., 30）

B: 3の倍数（3, 6, 9, ..., 30）

C: 5の倍数（5, 10, 15, ..., 30）

6.　積集合の演算子を使って、A,B,Cの積集合を計算します。変数名はintersection_ABCとします。

7.　積と差集合の演算子を使い「積集合からCを除いた部分」を計算します。変数名はintersection_AB_minus_C とします。同様に、Bを除いた部分、Aを除いた部分を計算します。 = A & B & C intersection_AB_minus_C = A & B - C intersection_BC_minus_A = B & C - A intersection_AC_minus_B = A & C - B 集合の交差と差集合を計算しています。&演算子は交差を、-演算子は差集合を表します。

11.　 AではあるがBでもCでもない集合、変数をdifference_A_minus_BC = A - B - Cとします。ここでは$A \setminus (B \cup C)$の式で計算していますが、次の式でも計算することができます。

14.　complement = (U - (A | B | C)) 全体集合Uに対するA, B, Cの和集合の補集合を計算しています。

15.　print(f'A & B & C = {intersection_ABC}') ... print(f'U - (A | B | C) = {complement}') 計算結果を出力しています。f-stringを使用して、各集合演算の結果を見やすく表示しています。

3つの集合のベン図

3つの集合の関係を見るためにベン図を描いてみます。

venn3による3つの集合のベン図を描く

from matplotlib import pyplot as plt
from matplotlib_venn import venn3
fig ,ax = plt.subplots()
diagram3= venn3([A , B, C], set_labels = ('A:multiples_of_2', 'B:multiples_of_3', 'C:multiples_of_5'))
plt.title('Venn Diagram of Multiples of 2,3 and 5 up to 30')
diagram3.get_label_by_id("100").set_text( "\n".join(map(str,difference_A_minus_BC)))
diagram3.get_label_by_id("010").set_text( "\n".join(map(str,difference_B_minus_AC)))
diagram3.get_label_by_id("001").set_text( "\n".join(map(str,difference_C_minus_AB)))
diagram3.get_label_by_id("110").set_text( "\n".join(map(str,intersection_AB_minus_C)))
diagram3.get_label_by_id("011").set_text( "\n".join(map(str,intersection_BC_minus_A)))
diagram3.get_label_by_id("101").set_text( "\n".join(map(str,intersection_AC_minus_B)))
diagram3.get_label_by_id("111").set_text( "\n".join(map(str,intersection_ABC)))
plt.text(0.6, 0.6, ' '.join(map(str,U- (A | B | C))), ha='right', va='top')
fig.set_facecolor('#e6f2ff')
plt.tight_layout()
plt.show()

Matplotlib（グラフ描画ライブラリ）の拡張ライブラリをインポートします。

6-12. diagram3.get_label_by_id("xxx").set_text("\n".join(yyy)) get_label_by_id メソッドを使用して、ベン図の特定の領域にアクセスし、set_text で内容を設定しています。"xxx" の部分は以下のように対応します：

"100": A のみの領域

"010": B のみの領域

"001": C のみの領域

"110": A と B の共通部分（C を除く）

"011": B と C の共通部分（A を除く）

"101": A と C の共通部分（B を除く）

"111": A, B, C の共通部分テキストは '\n'.join() を使用して複数の要素を改行で区切って表示しています。

plt.show() 作成したベン図を表示します。

$ n(A \cup B \cup C)$

$= n(A)+n(B)+n(C)- n(A \cap B) -n(A \cap C) -n(B \cap C)+n(A \cap B \cap C)$

$n(\overline{A\cup B \cup C})=n(U)-n(A \cup B \cup C)$

$=n(U)-n(A)-n(B)-n(C)+ n(A \cap B) +n(A \cap C) +n(B \cap C)-n(A \cap B \cap C)$

これは、ベン図を見ればよくわかります。

3つの集合での法則

3つの集合の積集合、和集合を3つ以上つなげた場合は、計算する順序によらず同じ結果になります。

結合法則 associative property

$A \cup B \cup C=(A \cup B) \cup C=A \cup(B \cup C)$

$A \cap B \cap C=(A \cap B) \cap C=A \cap(B \cap C)$

この法則は、ベン図を見れば明らからで、今後の計算で適用できるものとして考えます。ただし、結合法則が成り立つのは、和集合、積集合が同じ記号が並んだ時だけです。記号が混在するときには、次の分配法則が成り立ちます。

和集合と積集合が混在する場合は次のような法則が成り立ちます。

分配法則 distributive law

$A \cup(B \cap C)=(A \cup B) \cap(A \cup C)$

$A \cap(B \cup C)=(A \cap B) \cup(A \cap C)$

$(A \cap B) \cup C=(A \cup C) \cap(B \cup C)$

$(A \cup B) \cap C=(A \cap C) \cup(B \cap C)$

また、当たり前のようですが、冪等法則も注意が必要です。冪等法則は和集合と積集合についての法則がありますが、ここでは積集合の冪等法則を使います。

和集合の冪等法則　Idempotency of Union

$A \cup A =A$

積集合の冪等法則 Idempotency of Intersection

$A \cap A =A$

$(A \cap C) \cap (B \cap C) = A \cap B \cap C$

ここから、集合の数が3の場合の方除原理の計算は次の通りになります。

\begin{aligned} n(A \cup B \cup C) &= n((A \cup B) \cup C) \\ &= n(A \cup B) + n(C) - n((A \cup B) \cap C) \\ &= n(A)+n(B)- n(A \cap B) +n(C)-n((A \cap C) \cup (B \cap C)) \\ &= n(A)+n(B)- n(A \cap B) +n(C)-(n(A \cap C) +n(B \cap C)-n(A \cap C) \cap (B \cap C)) \\ &= n(A)+n(B)+n(C)- n(A \cap B) -n(A \cap C) -n(B \cap C)+n(A \cap B \cap C) \end{aligned}

写像からみた包除原理

①全体集合

空室も許した制約なしの重複順列$k^n$を計算します。全体集合Uは5人が3部屋を自由に選ぶことができるので$3^5=243$通りになります。

$n(U)= 3^5=243$

②1部屋以上空き部屋になる場合

Aが空き部屋になる集合Aの場合の数は5人をB, Cの部屋に割り振ることになるので、$2^5=32$通りになります。同じように、集合Bも集合Cも32通りになります。そこで空室が出ない重複順列は、全体集合からこれらA, B, Cの3つの集合の数の合計($32\times3=96$)を差し引くことで計算することができます。

$n(A)=n(B)=n(C)=2^5=32$

$243-32\times3=147$

③2部屋以上空き部屋になる場合

②で差し引いた中には (C, C, C)のように集合Aにも集合Bにも含まれる$n(A\cap B)$があり、その場合の数は$1^5=1$になります。$n(A\cap B)$は②で2重に差し引かれているので、逆に足し戻してやる必要があります。このようなものは$n(B\cap C)である(A, A, A), n(C\cap A)$である(B, B,B)の３つあります。

$n(A\cap B)=n(B\cap C)=n(C\cap A)=1^5=1$

$147+1\times3=150$

④3部屋以上空き部屋になる場合

集合の考え方からすると、ＡもＢもＣも空室の場合、$A\cap B\cap C$があれば、③で足し戻し過ぎになるので、さらに差し引く必要が生じます。もっとも今回は、全室空室はありえませんからここは0になります。

$n(A\cap B\cap C)=0^5=0$

$150-0 =150$

ベン図を課題に適用する

計算式は次の通りになります。

n=5,k=3のときの全射の重複順列の個数

$n(\overline{A\cup B\cup C})$

$=n(U)-\{n(A)+n(B)+n(C)\}$

$+\{n(A\cap B)+n(B\cap C)+n(C\cap A)\}-n(A\cap B\cap C)$

$=243-32\times3+1\times3-0=150$

部屋数が4の場合

関数による計算

k=4になると、さらに複雑になります。kがさらに増えることも見据えて検討します。組み合わせと件数を確認します。ここではn=7、k_list= ['A', 'B', 'C', 'D']とします。

４部屋の場合

n = 7
k_list= ['A', 'B', 'C', 'D']
perm_surjective_list = perm_surjective_func(k_list, n)
print('unrestricted = ',len(k_list)**n,'surjection = ',len(perm_surjective_list))
pprint.pprint(perm_surjective_list)

unrestricted =  16384 surjection =  8400
[('A', 'A', 'A', 'A', 'B', 'C', 'D'),
 ('A', 'A', 'A', 'A', 'B', 'D', 'C'),
 ('A', 'A', 'A', 'A', 'C', 'B', 'D'),
 ('A', 'A', 'A', 'A', 'C', 'D', 'B'),
  ・
・
('D', 'D', 'D', 'D', 'C', 'B', 'A')]

1.　#7と同じことをn=7,k=4として実行します。

集合論からk=4の包除原理を計算する

はじめに集合の定理から包除原理を計算します。まずは結論からいうと次のような式になります。

K=4の方除原理

$ n(A \cup B \cup C \cup D)$

$= n(A)+n(B)+n(C)+n(D)$

$-\{n(A \cap B)+n(A \cap C)+n(A \cap D)+n(B \cap C)+n(B \cap D)+n(C \cap D)\}$

$+\{n(A \cap B \cap C)+n(A \cap B \cap D)+n(A \cap C \cap D)+n(B \cap C \cap D)\}$

$-n(A \cap B \cap C \cap D)$

この計算式は次の通り、結合法則、分配法則、和集合の冪等法則を繰り返し適用することにより求めることができます。

\begin{aligned} n(A \cup B \cup C \cup D) &= n((A \cup B \cup C) \cup D) \\ &= n(A \cup B \cup C) + n(D) - n((A \cup B \cup C) \cap D) \\ &= [n(A)+n(B)+n(C)- n(A \cap B) -n(A \cap C) -n(B \cap C)+n(A \cap B \cap C)] \\ &\quad + n(D) - n((A \cup B \cup C) \cap D) \\ &= n(A)+n(B)+n(C)- n(A \cap B) -n(A \cap C) -n(B \cap C)+n(A \cap B \cap C) \\ &\quad + n(D) - n((A \cap D) \cup (B \cap D) \cup (C \cap D)) \\ &= n(A)+n(B)+n(C)- n(A \cap B) -n(A \cap C) -n(B \cap C)+n(A \cap B \cap C) \\ &\quad + n(D) - [n(A \cap D) + n(B \cap D) + n(C \cap D) \\ &\quad - n(A \cap B \cap D) - n(A \cap C \cap D) - n(B \cap C \cap D) + n(A \cap B \cap C \cap D)] \\ &= n(A)+n(B)+n(C)+n(D) - n(A \cap B) -n(A \cap C) -n(A \cap D) \\ &\quad -n(B \cap C) -n(B \cap D) -n(C \cap D) + n(A \cap B \cap C) \\ &\quad + n(A \cap B \cap D) + n(A \cap C \cap D) + n(B \cap C \cap D) \\ &\quad - n(A \cap B \cap C \cap D) \end{aligned}

かなり複雑な数式になります。さすがに地道に計算するのはここまでで、何かもっとうまい方法を見付けたくなります。

k=4の全射の重複順列を写像から計算する

k=4ともなると、matplotlibライブラリにも描くためのサブパッケージはありませんし、ベン図では対応できそうもありません。こんなときは写像の出番です。

①全体集合

空室も許した制約なしの重複順列$k^n$を計算します。全体集合Uは7人を4部屋に割り振る重複順列になるので$4^7=16384$通りになります。

$n(U)=4^7=16384$

②1部屋以上空き部屋になる場合

1部屋以上が空きになるのは、図の左側のようにAが空きになるケースや、右のようにBが空きになるケースが考えられます。このほか、当然C,Dが空き部屋になる場合もあるので合計4ケースになります。

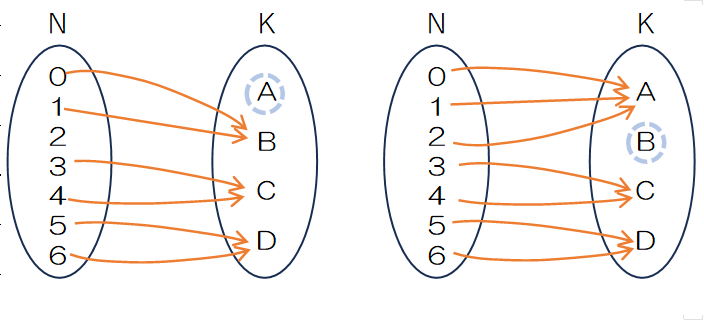
この4つのケースのうち1つ、図の左側のように7人をB, C, Dの3部屋に割り振るので、$3^7=2187$通りになります。同じように、集合B、C、Dも2187通りになるので、空室が出ない重複順列は全体集合 ($2187\times4=8748$)を差し引くことで計算することができます。

$ n(A)=n(B)=n(C) =n(D)= 3^7=2187$

$16384-2187\times4=7636$

一般論として、全射の計算をするため全体集合から加減するときには、次の式で計算します。

空室以外の部屋の組み合わせ（A,B,C,Dのうち3つ$\ _4 C_3 $）×組み合わせ毎の重複組み合わせの数($3^7$)

③2部屋以上が空きになる重複順列を足し戻す

図のようにAもBも空き部屋になる$A\cap B$のようなケースでは、①では1でカウントされていますが、②ではAとBでも二重に差し引かれてしまいます。この不都合を解消するために、いったん差し引いたものを足し戻す必要があります。同様に$A\cap C, A\cap D,B\cap C, B\cap D, C\cap D $を合わせて6ケース、つまり4つの部屋から2つを選ぶので$\ _4 C_2 $通りとなります。

その6ケースのうち1つ、$A\cap B$では C,Dの2部屋に7人が泊まることになるので$2^7=128$通りとなります。このため、6ケース×128=768通りを足し戻す必要があります。

$ n(A\cap B)=n(A\cap C)=n(A\cap D) =n(B\cap C) =n(B\cap D) =n(C\cap D)=n2^7=128$

$7636+128\times6=8404$

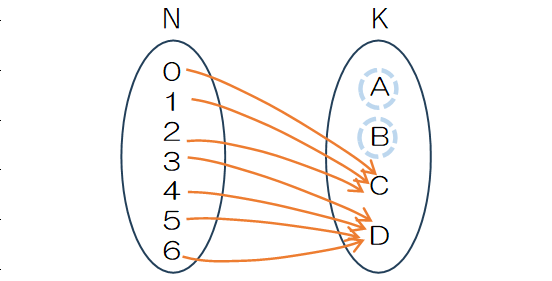
④3部屋以上が空きになる重複順列を再び差し引く

図のようにAもBもCも空き部屋$A\cap B\cap C$では③で重複して「足し戻し過ぎ」の状態にあるので、再び差し引く必要があります。

同様に$A\cap B\cap D, A\cap C\cap D, B\cap C\cap D $を合わせて4ケース、つまり4つの部屋から3つを選ぶので$\ _4 C_3 $通りとなります。

その4ケースのうち1つ、$A\cap B\cap C$では Dの1部屋に7人が泊まることになるので$1^7=1$通りとなります。このため、4ケース×1=4通りを再度、差し引く必要があります。

$ n(A\cap B\cap C)= n(A\cap B\cap D)= n(A\cap C\cap D)= n(B\cap C\cap D) =1^7=1$

$8404-1\times4=8400$

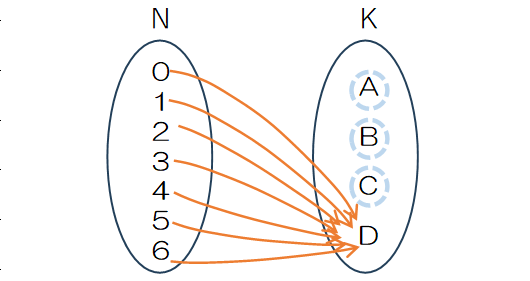
⑤4部屋以上が空きになる重複順列があれば差し引く

もし、AもBもCもDも空き部屋という重複順列があれば、引きすぎたものを再度足し戻す必要があります。もっともn=4の場合は0になるので、考える必要はありません。

$n(A\cap B\cap C\cap D)=0^7=0$

重複順列$4^5=16384$通りのうち、全射のものは8400通りになります。

$ n(A \cup B \cup C \cup D)$

$= n(A)+n(B)+n(C)+n(D)$

$-\{n(A \cap B)+n(A \cap C)+n(A \cap D)+n(B \cap C)+n(B \cap D)+n(C \cap D)\}$

$+\{n(A \cap B \cap C)+n(A \cap B \cap D)+n(A \cap C \cap D)+n(B \cap C \cap D)\}$

$-n(A \cap B \cap C \cap D)$

$n(U)=4^7=16384$

$n(A)=n(B)=n(C)=n(D)=3^7=2187$

$n(A\cap B)=n(A\cap C)=n(A\cap D)=n(B\cap C)=n(B\cap D)=n(C\cap D)=2^7=128$

$n(A\cap B\cap C)=n(A\cap B\cap D)=n(A\cap C\cap D)=n(B\cap C\cap D)=1^7=1$

$n(A\cap B\cap C\cap D)=0^7=0$

$n(A \cup B \cup C \cup D)=2187\times4-128\times 6+1\times 4-0=7984$

$n(\overline{A\cup B\cup C\cup D})=n(U)-n(A \cup B \cup C \cup D)=16384-7984=8400$

全射の場合の数の計算

ここまで複雑になると何度も引いたり足し戻したりしていて、本当に正しく計算されているか不安になります。そこで、全射の条件を満たさない2例について最終的に差し引かれるまでの流れを整理します。

(D, D, D, D, D, D, D)のようなに集合A,B,Cに当てはまるケース

①では制約なしの全体集合を計算しているので1でカウントされていますが、全射の条件を満たしていないの②～④の計算の結果、最終的に0に落ち着かせることが必要になります。

②では集合A,B,Cとして3回（$\ _3 C_1 $）差し引かれています。

③では$A\cap B$、$A\cap C$と$B\cap C$の3回（$\ _3 C_2 $）で足し戻されています。

④では$A\cap B\cap C$（$\ _3 C_3 $）で1回、再度差し引かれます。

よって1-3+3-1=0となり思った通りの結果になります。

ここで①は常に1なので$\ _3 C_0$と考えることができます。ところで、$\ _3 C_0 - \ _3 C_1+ \ _3 C_2 - \ _3 C_3 =1-3+3-1=0$となるのでうまく計算できたことがわかります。

(C, D, D, D, D, D, D)のようなに集合A,Bに当てはまるケース

①では制約なしの全体集合を計算しているので1でカウントされています。

②では、A,Bとして2回（$\ _2 C_1 $）差し引かれています。③では、$A\cap B$として足し戻されます。結果$\ _2 C_0 - \ _2 C_1+ \ _2 C_2=1-2+2=0$となりやはり正しく計算されています。

この考え方を拡張するとkがもっと大きくなっても、空き部屋の数をv、差し引く集合の重複数をiとすると、最終的に重複順列としてカウントされるのは、次の式で計算することができます。この式の値は$(x-1)^x$を二項定理にあてはめて展開し、$x=1$を代入して計算することができます。

空き部屋がいくつでカウントされるか

$\sum\limits_{i=0}^{x}(-1)^i\,\ _{x}C_i=\ _x C_0 -\ _x C_1+\ _x C_2-\ _x C_3+\cdots \pm\ _x C_x=0 $ただし$x=0$のときは1

vが奇数の時はマイナス、偶数の時はプラス

二項定理と重複順列の全射が思わぬところで結びつきました。

重複順列の全射の場合の数を計算する関数

最後に、全射の重複順列の場合の数の計算方法を一般化してみます。

部屋の数k=4に対して空き部屋の数をiとします。人数が6人なので、制約なしの場合、重複順列は$4^6$となります。

①の制約なしの場合、$k^n$となりますが、このとき空き部屋は0なのでi=0となります。これ以降の加減は表の通りになります。タイプには、代表的なものを示していますが、これを見ればそれぞれの組み合わせが$\ _k C_i$であることがわかります。また、k=0のときに＋、これ以降は交互にプラスとマイナスを繰り返すので$(-1)^i$であらわします。表を見ると数式は図の通りになります。

このような計算方法を包除原理（Inclusion-exclusion principle）といい、全射の計算で威力を発揮します。

これまで例で取り上げた重複順列について、前節の式をあてはめてみました。

重複組み合わせの全射の個数

$\sum\limits_{i=0}^{k}(-1)^i\,\ _{k} C_i(k-i)^n=\ _{k} C_0k^n-\ _{k} C_1(k-1)^n+\ _{k} C_2(k-2)^n- \cdots\pm\ _{n} C_n(n-n)^n $

上記の計算式を使い、全射の重複順列の個数を計算する関数を作成します。関数名は順列の全射という意味で、perm_surjection_countとし、引数はこれまでと同じようにk,nとします。また、関数を使い、これまで検討した3ケースについて計算し検証します。

# 全射の重複組み合わせの件数を計算

def perm_surjection_count(k, n):
sigma = 0
for i in range(k+1):
sigma += ((-1)**i) * comb(k,i) * (k-i)**n
return int(sigma)
print(perm_surjection_count(2, 5))
print(perm_surjection_count(3, 5))
print(perm_surjection_count(4, 7))

30
150
8400

4.　数式を当てはめます。

これまでに3つの例を挙げて計算してきましたが、結果は合致していることがわかります。計算式は正しそうですが、さらに詳しい証明も欲しくなります。このあたりはまた別の機械に譲ります。

全単射としてのn=kの順列

N=kの順列

重複順列、順列の仕上げとして全射と単射の両方の要件を満たす全単射の例を取り上げます。概要を把握するため、次の問題を考えます。

問題4

4人の学生が合宿でそれぞれ個室に泊まることとします。宿舎にはK={A, B, C, D}の4部屋が用意されており、学生は出席番号で表し、N={0, 1, 2, 3}としたときの部屋割りとして考えられる順列を生成し、その場合の数を計算してください。

写像で表すと次のようになります。

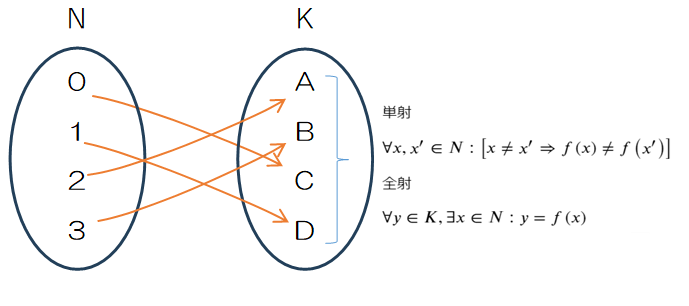
個室になるということは単射である順列になり、なおかつn=kであることから空き部屋が出ることがないので全射の重複順列になり、併せて全単射になります。

そこで、順列を生成するperm_injective_func関数を使いperm_injective_listを、全射の重複順列を生成するperm_surjective_func関数を使いperm_surjective_listを生成し比較します。

N=Kの場合の全単射の考え方

k_list = ['A', 'B', 'C', 'D']
n = 4
perm_injective_list = perm_injective_func(k_list, n)
perm_surjective_list = perm_surjective_func(k_list, n)
if perm_surjective_list == perm_injective_list:
print('surjective == injective')
print('surjective = ',len(perm_surjective_list))

surjective == injective
surjective =  24

perm_surjective_list == perm_injective_listの場合はその旨を表示します。

結果は包除原理を使った全射による個数も順列の計算を使った単射による個数も一致することがわかりました。

全射の個数

$\sum\limits_{i=0}^{n}(-1)^n\,\ _{n} C_i(n-i)^n=\ _{n} C_0n^n-\ _{n} C_1(n-1)^n+\ _{n} C_2(n-2)^n-\cdots\pm\ _{n} C_n(n-n)^n $

$=\ _{4} C_0 4^4-\ _{4} C_1 3^4+\ _{4} C_2 2^4-\ _{4} C_3 1^4+\ _{4} C_4 0^4=24$

単射の個数

$n!=4!=24$

上記のように、生成する重複順列は一致し、個数は24個になります。上記の式が包除原理の結果と階乗の計算結果が等しくなるは不思議ですが、このあたりを突き詰めていくと面白い世界が見えてきます。

モンモール問題の概要

モンモール問題の計算

n=kの順列で特殊なものとして、モンモール問題という興味深いものがあります。フランスの数学者ピエール・モンモールにちなむもので、突き詰めていくと非常に興味深い洞察を得ることができます。ここでは、そのさわりのみをご紹介します。

問題5

5人でプレゼントの交換会をします。N={A, B, C, D, E}の5人が１つずつ別々のプレゼントを持ち寄り、でたらめに交換します。この際、自分が持参したプレゼントを受け取ることが1人もないような場合の数を計算してください。

ここで生成される順列を完全順列complete permutations、攪乱順列（derangement）といろいろな呼び方がありますが、今後は、攪乱順列という名前で通します。また、攪乱順列の個数をモンモール数（Montmort number）といいます。攪乱順列は写像にすると次のようになります。集合Nから同じ要素の集合Kへの対応となりますが、このような写像を自己写像（self-map）といいます。要素A,B・・の後にある数字はプログラムを作成するときに使用する要素の順番を付けたものです。

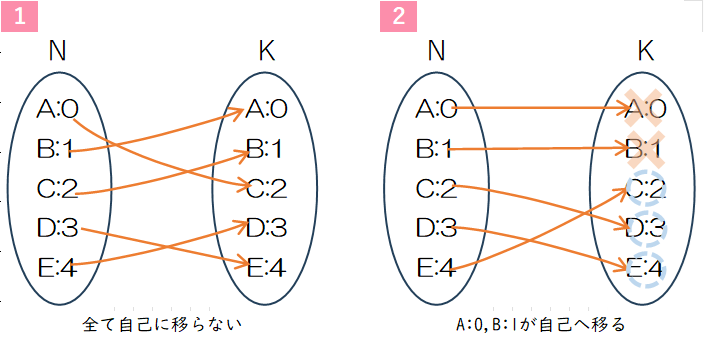
図表の１は攪乱順列の例で、全ての人がほかの人からプレゼントをもらっています。一方２は、AとBが自分は持ち寄ったプレゼントを受け取ることを示しており、順列ではあるけど錯乱順列ではない例になります。

モンモール問題についてはSymPyライブラリのsubfactorial関数を使い、モンモール数を計算することができます。subfactorialはまさにモンモール数を表す階乗の1つで!nのように会場の逆の表記の方法もあります。

subfactorial関数は集合の要素数を引数とします。一方、generate_derangements関数を使い、完全順列を生成することができます。この場合、集合の要素をリストなどの形式を引数とします。

モンモール数を生成する関数

from sympy import subfactorial
from sympy.utilities.iterables import generate_derangements
k_list=['A','B','C','D','E']
n=len(k_list)
sympy_derangements_list = list(generate_derangements(k_list))
print('sympy_derangements(5) =',subfactorial(n))
pprint.pprint(sympy_derangements_list)

sympy_derangements(5) = 44
[['B', 'A', 'D', 'E', 'C'],
 ['B', 'A', 'E', 'C', 'D'],
 ['B', 'C', 'A', 'E', 'D'],
・・
['C', 'A', 'B', 'E', 'D'],
・・
['E', 'D', 'A', 'C', 'B'],
 ['E', 'D', 'B', 'A', 'C'],
 ['E', 'D', 'B', 'C', 'A']]

1.　subfactorial関数はSymPyライブラリからインポートします。

2.　generate_derangements関数はSymPyライブラリのsympy.utilities.iterablesモジュールからインポートします。

要素数5のモンモール数は44であることがわかります。

次に、完全順列を生成する関数を作成します。順列を生成するperm_injective_funcをもとに、次の変更を加えます。

引数はn=kより集合Nのリストを渡すのみとします。順列の候補として配列に追加する際に、順列にするために同じ要素のものとともに配列のインデックスと要素の順番が同じ場合は配列に加えないようにします。

完全順列を生成する関数

def perm_derangements_func(k_list):
array = [[]]
for cnt in range(len(k_list)):
temp = array
array = []
for elm in temp:
for num,item in enumerate(k_list):
if item not in elm and cnt != num:
array.append(elm + [item])
return array
perm_derangements_list = perm_derangements_func(k_list)
if perm_derangements_list == sympy_derangements_list:
print('perm_derangements_lis == sympy_derangements_list')

perm_derangements_lis == sympy_derangements_list

8.　リストでの順番とk_listの順番が等しい場合は攪乱順列にならないのでarrayには追加しません。

モンモール数の計算と包除原理

モンモール数は包除原理を使って計算することができます。

はじめに、n=5のときの集合Nから集合Kへの順列は$5!=120$になります。これに対して、Aの1人だけ自分が持ち寄ったプレゼントを受け取ってしまうケースは３のようになるので、4!通りになります。おなじように４はBが同じ目に遭うケースです。このように、$5!-5\times 4!$で計算することができます。ところが、前図の２のように上記の計算ではA,Bが自分が持ち寄ったプレゼントを受け取ることになるので、その数3!を足し戻す必要があります。

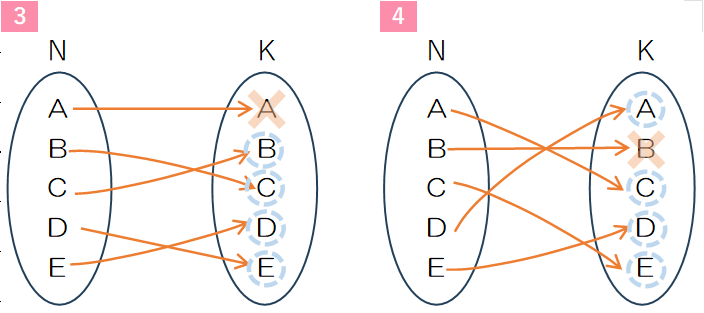
この計算は最終的には、全ての人が自分が持ち寄ったプレゼント受け取るという稀有なケースまで続きます。

この結果、モンモール数は次の式により計算することができます。

$\sum\limits_{i=0}^{n}(-1)^i\,\ _{n} C_i(n-i)!=\ _{n} C_0n!-\ _{n} C_1(n-1)!+\ _{n} C_2(n-2)!-\cdots\pm\ _{n} C_n(n-n)!$

$=\ _{5} C_0 5!-\ _{5} C_1 4!+\ _{5} C_2 3!-\ _{5} C_3 2!+\ _{5} C_4 1!-_{5} C_5 0!=$

$=120-12-+60-20+5-1=44$

それでは、モンモール数を生成する関数を作成します。

包除原理でモンモール数を計算する関数

def montmort_number_count(n):
sigma = 0
for i in range(n+1):
sigma += ((-1)**i) * comb(n,i) * factorial(n-i)
return int(sigma)
montmort_number_count(5)

4.　n=kなのでそのまま計算します。

まとめ

これまで、区別のある学生を区別のある部屋に割り振ることを題材に写像の考え方を見てきました。重複順列、順列を写像という視点でまとめてみました。この際に、特に制限の場合、全射、単射の3つのパターンがあることを見てきました。個数は次の式により計算することができます。

制約なし	単射	全射
重複順列	順列	包除理論による全射
$_k\prod{_n}=k^n$	$\ _k P_n =\frac{k!}{(k-n)!}$	$\sum\limits_{i=0}^{k}(-1)^i\,\ _{k} C_i(k-i)^n$