重複順列を写像で捉え、Pythonで生成する
重複順列の考え方
重複順列(permutation with repetition)について理解するため、次の問題を考えます。
Example 1.1
5人の学生が合宿で2つの部屋に分かれて泊まることとします。各学生はどの部屋でも自由に選ぶことができるので、空き部屋ができることもあります。5人の学生は出席番号で表し、$N=\{0, 1, 2, 3, 4\}$とします。また、部屋名は$K=\{A, B\}$としたとき、部屋割りとして考えられる重複順列を生成し、その数を計算してください。
初歩的な問題ですが、写像の概念を使って整理していきます。
写像からみた重複順列
重複順列などの場合の数においては、定義域を集合 $N$ 、終域を集合 $K$ として、集合 $N$ から集合 $K$ への写像と捉えます。
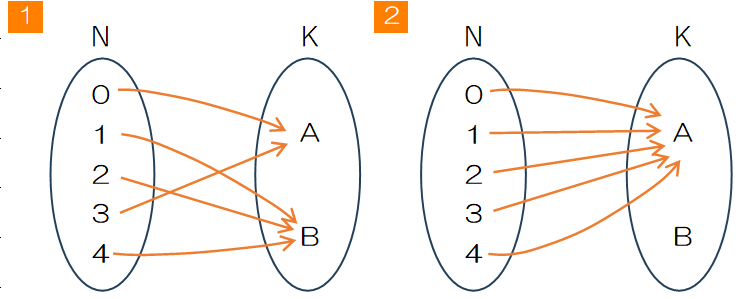
Figure 1.1の
Figure 1.1の
このため、重複順列は集合$N$、$K$ともに相異なる集合について全射・単射の制限がない任意写像になります。
重複順列の生成と個数の計算方法
0 が A,B の 2通りの部屋を選び、その各場合について 1 が 2通り、さらにその各場合について 2 が $2\times2=2^2=4$通り、というように 0 から 4 までの 5 人に対して繰り返すので、$2^5=32 $通りになります。
Equation 1.1 重複順列の個数
最終的には、図の右側のように5人がどの部屋に泊まるかを 32 個のタプルとして生成し、1 つのリストとしてまとめます。重複順列の数は $k^n$ (k の n 乗)により計算することができ、この計算式は"k to the n-th power"と読みます。なお、$\prod$ は積を表す数学記号です。
Python による重複順列の生成と個数の計算
Python の関数の分類
重複順列を生成する関数について論じる前に、前提知識としてPython の関数の4つの分類を確認しておきます。
① 組み込み関数
print関数や len関数、input関数など頻繁に使用する関数です。Python を起動時に主記憶装置にロードされ、すぐに使用することができます。
② 標準ライブラリにある関数
今回使用するitertools関数を提供するモジュール関数型プログラミング用モジュール(Functiona Programming Modules)や math モジュールを提供する数値と数学モジュール(Numeric and Mathematical Modules)などがあります。Python 本体に含まれていますが、使用する場面は組み込み関数ほど多くありません。そこで、Pythonを起動するごとに1度だけimport文を使い読みこまないと使用できない仕組みとなっています。このことにより、Pythonの起動時間を短縮するとともに、使用しない機能が主記憶装置を占有することを防いでいます。
③ 外部ライブラリにある関数
数式処理や代数計算を行う SymPyライブラリ や、科学技術計算を行う SciPyライブラリになど、さまざまな組織が特化したニーズに対応した外部ライブラリを開発しています。外部ライブラリにある関数を使用するためには、PyPI (Python Package Index)というサイトから追加でインストールし、さらにPython を起動するごとに import 文を使って読み込む必要があります。このテキストでは、②の標準ライブラリと③の外部ライブラリのうち広く使われているものを合わせて既存のライブラリと呼ぶこととします。
④ 自作関数
既存のライブラリでは実現できない処理が必要な場合には、Python の機能を組合せて自分で関数を作成します。
このテキストでは、写像に関わる様々な計算を既存のライブラリを使って実行し、その後で自作関数を作成して結果を照合し、正しく計算できているか確認します。さらに、既存のライブラリでは実現できないような計算へと発展させます。
既存のライブラリによる重複順列の生成
itertools モジュールの product関数による重複順列の生成
itertools モジュールが提供する product関数を使用することにより重複順列を生成することができます。product関数は出力結果がリストではなく、イテレータと呼ばれるデータを 1 つずつ順番に取り出す形式で出力する仕様になっています。
product関数で重複順列を生成するときは、集合 $N$ の要素数 n を引数 repeat=n として渡します。戻り値として $0,1, \cdots 4$ が選んだ部屋が A か B かを表すイテレータが生成されます。
Code 1.1 itertools モジュールの product 関数による重複順列の生成
- import itertools
- k_list = ['A', 'B']
- n = 5
- itertools_product = itertools.product(k_list, repeat = n)
- print(f'type of itertools_product = {type(itertools_product)}')
- for product in itertools_product:
- print(product)
type(itertools_product) = class itertools.product
[('A', 'A', 'A', 'A', 'A'),
('A', 'A', 'A', 'A', 'B'),
(中略)
('A', 'B', 'B', 'A', 'A'),
('A', 'B’, 'B', 'A', 'B'),
(中略)
('B', 'B', 'B', 'B', 'A'),
('B', 'B', 'B', 'B', 'B')]
1. product関数は標準ライブラリのitertoolsモジュールの1つなので、使用するためにはPythonを起動するごとに1度だけインポートする必要があります。
4. product関数でk_listのn回の直積を計算し、戻り値を変数itertools_productに代入します。
5. product関数の型を出力します。itertools.product classという特殊なイテレータの形式になります。
6. イテレータの内容を出力するためには、for文を使って要素を1つずつ順番に取り出し、print関数で出力する必要があります。
itertools.product は、イテレータと呼ばれる特別なデータ型で、データをあらかじめ全て主記憶領域(メモリ)に保存するのではなく、必要なときに 1 つずつ順番に作って処理し、使い終わったデータは消える仕組みです。このため、主記憶領域を無駄なく使えるという利点がありますが、同じデータを再度参照するためには、もう一度最初から生成し直す必要があります。このため、出力結果を何度も参照する場合には list関数を使いリストに変換します。
Code 1.2 イテレータをリストに変換し個数を数える
- itertools_product_list = list(itertools.product(k_list, repeat=n))
- print(
- f'count of itertools.product ({len(k_list)}, {n}) : '
- f'{len(itertools_product_list)}'
- )
count of itertools.product (2, 5) : 32
1. イテレータをリスト形式に変換するためにはlist関数を使用します。
2. print関数のコードが長くなる場合は、”print(“として、”(“をつけて行を分割します。
5. 行を分割した場合、最後の行で”)”を記述します。
$2^5=32$ 通りと結果が一致しました。
シーケンスによる写像の表現
このテキストでは、さまざまな種類の順列や組合せを生成します。ある条件を満たす順列や組み合わせは複数個あるのが通常なので、リストの中に複数のタプルやリストを包み込む入れ子(nest)構造にします。入れ子がn段階になっているリストをn次元リストと呼び、ネストの階層は外側の大きなリスト”[ ]”が第1階層、内側の写像を表すタプルが第2階層というように表現します。今後、さまざまな写像を生成しますが、多くの場合には2次元リストになりますが、写像がさらに深い階層になり、全体で3次元以上のリストになることも考えられます。
[ ・第1階層開始 タプルのリスト
('A', 'A', 'A', 'A', 'A') , 第2階層 タプルorリスト →シーケンス
('A', 'A', 'B', 'A', 'B'),
・・・
('B', 'B', 'B', 'B', 'B')
] ・第1階層終了
プログラムを作成する上では第一階層をタプルのリスト (list of tuples)と呼び、変数名は順列の場合はperm_list、組合せの場合はcomb_listというように命名します。原則タプル(一部リストの場合もある) で('A', 'A', 'B', 'A', 'B')のように表記し,インデックスが集合$N$の要素となり、各々がどの集合Kの要素に対応付けられるかをしめします。多くの場合には集合$N$は0からn-1のn個の要素の集合として、その要素に対応づけられる集合Kの要素を示すタプルを(A,B,B,A,B)は2に該当します。つまり0→Aの対応を示します。
Pythonではリストやタプルなど一定の条件を満たすものをシーケンス(sequence)と呼んでいます。そこで、今後はシーケンスの名称としてseqという変数にします。
各シーケンスの中で'B'のような個々の要素elementですがelemという変数を使います。一方、k_list=['A', 'B']とした場合は要素のリストの要素という意味でitemという変数を使います。したがって、プログラムにおいてはk_listの中からitemを選び出しseqのelemに追加する処理を繰り返すことになります。
Pythonのシーケンスの特徴とその特徴により写像を表す際に便利で理由を示します。
①for文で順次読み込むことができる
このことにより集合Nに対応づけられる集合Kの要素を順を追ってもれなく調べることができます。
②インデックスアクセス、スライスを使うことができる
インデックスが使えるので集合Nの特定の要素に対応づけられる集合Kの要素を直接に調べることができます。
③len関数を使い個数を数えることができる
ある条件を設定した場合、それを満たす写像が複数存在するのが一般的です。このとき、その個数を数えることとがテーマになります。このとき、第1階層のリストにlen関数を適用すると写像の個数を簡単に調べることができます。
なお、リストやタプルの他、シーケンスには文字列 (string)や数字の範囲を示すrangeオブジェクトがあります。
重複順列を生成する自作関数
重複順列を生成する関数を作成し、product関数と実行結果を比べます。
重複順列を生成する自作関数の流れ
この関数は、指定された要素リスト k_list に基づいて、要素数 n の重複順列(順序付きの直積)を生成します。生成のために n 回ループを行い、次の通り各ループで 1 つずつ要素を追加していきます。
たとえば k_list = ['A', 'B'] のとき、
1 回目のループ後: [(A,), (B,)]
2 回目のループ後: [(A, A), (A, B), (B, A), (B, B)]
3 回目のループ後: [(A, A, A), (A, A, B), (A, B, A), (A, B, B), …]
4 回目のループ後: [(A, A, A, A), (A, A, A, B), (A, A, B, A), (A, A, B, B), …]
ここでは次の樹形図に従い重複順列を生成します。なお、
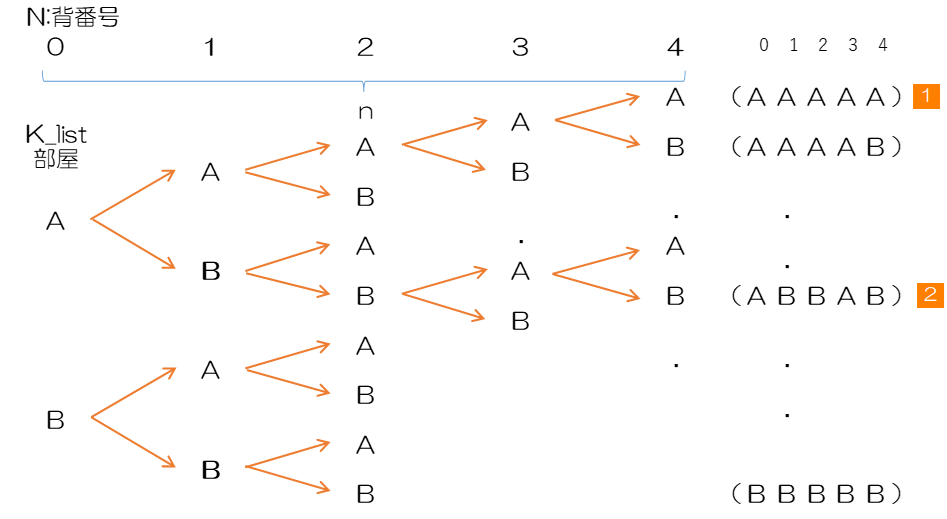
上記の流れで重複順列を生成するために、プログラムの流れを考えます。
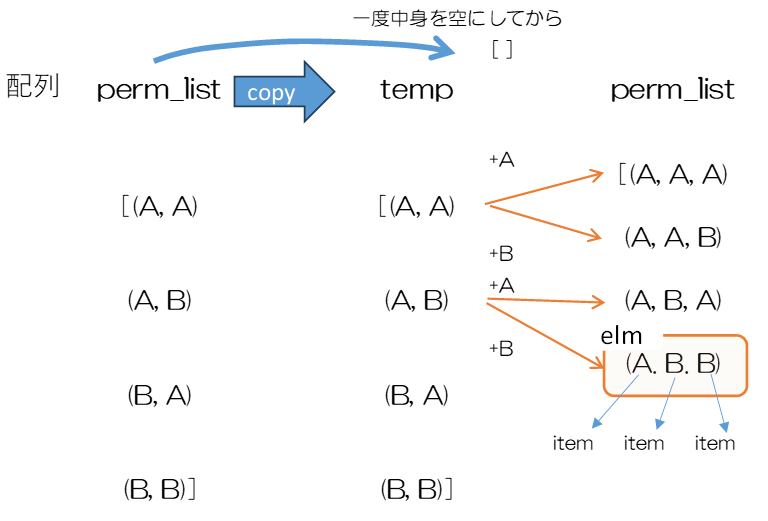
2 回目の要素の生成が完了し、3 回目のループの流れを示しています。
このように、要素数を増やすたびに perm_list と next_perm を切り替えながら処理を続けます。2 つのリストを使うので記憶領域が 2 倍必要になりますが、1つのリストで済まそうとすると、シーケンスを順次読み込みながら、同じリストにシーケンスを追加する必要があるので、永久ループに陥る恐れがあります。このため、リストに読み込みながら同じリストにデータを追加することは避けるのが原則です。
重複順列を生成する関数の作成
重複順列を生成する関数を作成します。関数名は全体写像( arbitrary)の順列(permutation)という意味で generate_ arbitrary_perm関数とし、itertools と同様に k_list と n の 2 つの引数として渡します。
Code 1.3 重複順列を生成する関数
- def generate_arbitrary_perm(k_list, n):
- perm_list = [()]
- for _ in range(n):
- next_perm = []
- for seq in perm_list:
- for item in k_list:
- next_perm.append(seq + (item,))
- perm_list = next_perm
- return perm_list
- arbitrary_perm_list = generate_arbitrary_perm(k_list, n)
- print(
- f'generate_arbitrary_perm({len(k_list)}, {n}) ='
- f'{len(arbitrary_perm_list)}'
- )
generate_ arbitrary_perm(2, 5) : 32
2. perm_list を初期化する際に、空のタプルを要素として持つリストとして定義します。4.で next_perm にコピーし、6.で制作途中の重複順列を読み込む際に何かしらのタプルがないとエラーになるためです。タプルは()+(1,)→(1,)となります。
3. for 文において、繰り返す回数を指定すればよく、処理中に何回目という管理が不要な時は、for _ のようにアンダースコアを使用します。
4.~8.により次のように、重複順列の生成途中のタプルを追加する処理を n 回繰り返します。
5. リスト perm_list から作成途中のタプルを seq として取り出し、k_list から取り出した item を右側に結合し next_perm に追加します。要素が 1 つだけのタプルは (item,) のように括弧の中で変数にカンマを付けます。
重複順列の各重複順列は、タプルにします。タプルはリストとは異なり、1 度作ると変更することができません。このような性質をイミュータブル(変更不可)と呼び、ミュータブル(変更可能)であるリストよりも構造が単純であるため、マシンへの負荷が少なくなります。また、イミュータブルであることは不便な面もありますが、作成したシーケンスを参照しながらいろいろな処理をする過程で、意図せず変更されてしまうようなエラーが発生するリスクが少なくなるというメリットもあります。
itertools の product関数と結果を比較
Code 1.2において itertools の product関数で生成しリストに変換した arbitrary_perm_list と、Code 1.3において自作関数で生成した arbitrary_perm_list を比較し、一致していればその旨を表示します。
Code 1.4 product関数と自作関数の結果を比較
- if arbitrary_perm_list == itertools_product_list:
- print('perm_ arbitrary_list == itertools_product_list')
perm_ arbitrary_list == itertools_product_list
1. 2 つのリストが示す重複順列は同じでも、並び順が異なると等しいと判断されません。この場合には、リストを並べ替えて比較し、等しくなれば重複順列は等しいと判断します。
ここでは、ソートをしなくても等しいと判断されました。両者とも同じ考え方でリストを生成していることが伺えます。
このことにより、perm_list が長さ $n$ の重複順列のリストとして返します。最終的に product関数の結果と一致します。作成の過程のリストを next_perm で仮置きして、perm_list と置き換えながら重複順列を生成するので、今一つ洗練されていない印象がありますが、これ以上シンプルなプログラムを作成するのは意外と困難です。
デカルト積を生成する関数
itertools によるデカルト積の計算
product 関数はそもそも、直積、デカルト積、Cartesian product)を生成する関数で、2 つ以上の集合の要素間で総当たりの組合せを生成します。例えば、洋服のタイプとして、T-Shirt, Sweater があり、それぞれにサイズと色があり、これらの全ての組合せがデカルト積になります。
Code 1.5 itertoolsモジュールのproduct関数でデカルト積を生成
- types = ['T-Shirt', 'Sweater']
- sizes = ['L', 'M', 'S']
- colors = ['Red', 'Blue', 'Green']
- itertools_product = list(itertools.product(types, sizes, colors))
- itertools_product
[('T-Shirt', 'L', 'Red'),
('T-Shirt', 'L', 'Blue'),
('T-Shirt', 'L', 'Green'),
('T-Shirt', 'M', 'Red'),
('T-Shirt', 'M', 'Blue'),
('T-Shirt', 'M', 'Green'),
('T-Shirt', 'S', 'Red'),
('T-Shirt', 'S', 'Blue'),
('T-Shirt', 'S', 'Green'),
('Sweater', 'L', 'Red'),
('Sweater', 'L', 'Blue'),
('Sweater', 'L', 'Green'),
('Sweater', 'M', 'Red'),
('Sweater', 'M', 'Blue'),
('Sweater', 'M', 'Green'),
('Sweater', 'S', 'Red'),
('Sweater', 'S', 'Blue'),
('Sweater', 'S', 'Green')]
4. types, sizes, colors の 3 つのリストを引数として指定すると 3 つのリストの各要素の直積を生成することができます。
重複順列と同様にここでは k_list を 5 つの集合として捉え、直積を取るので repeat=5 としています。その意味では product関数の特殊な使い方といえます。
デカルト積を生成する関数を作成
itertoolsのproduct関数と同じようにデカルト積をリストで生成する関数を作成します。ここで”*k_list”のように”*”からはじまる仮引数を可変長引数と呼びます。デカルト積のように、対象とする集合の数が可変であるときに使用され、引数をカンマ(”,”)で区切って関数に渡すと、関数の中では複数のリストを指定することができます。関数名は generate_cartesian_product とし、同じ条件でデカルト積を生成し、product 関数の出力結果と比較します。デカルト積では例のように 2 つ以上のリストについて計算する場合もあるので、リストの数が定まりません。この場合、仮引数に * を付け *k_lists とすると、引数の数を必要に応じて指定することができます。関数の中では*を取り k_lists という変数名になり、引数として渡した複数のオブジェクトの外側に包んだタプルになり、 for 文で順次取り出し処理することができます。
Code 1.6 デカルト積を生成する関数
- def generate_cartesian_product(*sets):
- product_list = [()]
- for current_set in sets:
- next_product = []
- for seq in product_list:
- for item in current_set:
- next_product.append(seq + (item,))
- product_list = next_product
- return product_list
- if (
- itertools_product
- == generate_cartesian_product(types, sizes, colors)
- ):
- print('itertools_product == generate_cartesian_product')
itertools_product == generate_cartesian_product
1. 引数は複数のリストという意味を込めて *k_lists とします。
3. k_lists から current_list としてリストを順次取り出します。
両者が一致していることを確認することができました。
