全射の重複順列

全射の重複順列について、写像と Python を使って整理します。制約なしの場合に比べ全射となると複雑な計算が必要になります。

ここからが山場です。全射の考え方を理解するため次の問題を考えてみましょう。

Example 1.4

学生が合宿で複数の部屋に分かれて泊まることとします。各学生は、どの部屋を自由に選んでよいものとしますが、空き部屋が出ることは許されません。学生は出席番号を集合$N$とし、部屋を集合$K$として、次の場合の部屋割りとして考えられる重複順列を生成し、その数を計算してください。

(1)$N=\{0, 1, 2, 3, 4\}$ $K=\{A, B \}$

(2)$N=\{0, 1, 2, 3, 4, 5\}$ $K=\{A, B , C\}$

(3)$N=\{0, 1, 2, 3, 4, 5, 6\}$ $K=\{A, B , C, D\}$

この考え方は包除原理と呼び、とても奥深いものがあります。

任意の写像の重複順列を全射にする

任意の写像から全射の写像の抽出

写像で見る全射の重複順列

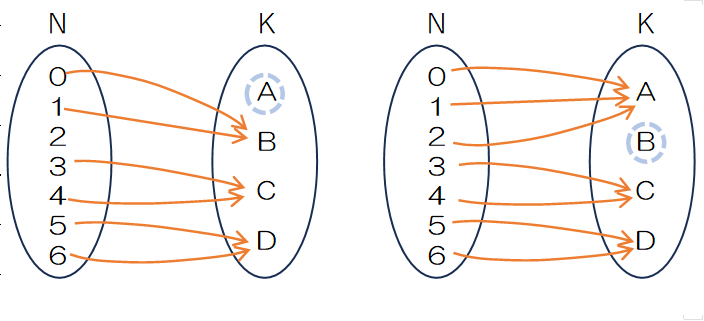
Figure 1.13 では全学生が部屋 A 、または部屋 B に集中している重複順列が見られます。宿の方がせっかく 2部屋を確保してくれたのに、空き部屋にしてしまうのでは品格を疑われてしまいます。そこで、少なくとも 1部屋に 1 人は泊まるような重複順列を考えます。全射とは、写像の終域のすべての要素が、定義域のある要素から対応づけられていることを要求する、すなわち、終域の中に、対応する定義域の要素が存在しない要素があってはならないのが全射（surjective）です。Figure 1.13 の１のような (A, A, B, A, B) は問題ありませんが、２のように (A, A, A, A, A) や、(B, B, B , B, B) のような重複順列は対象になりません。

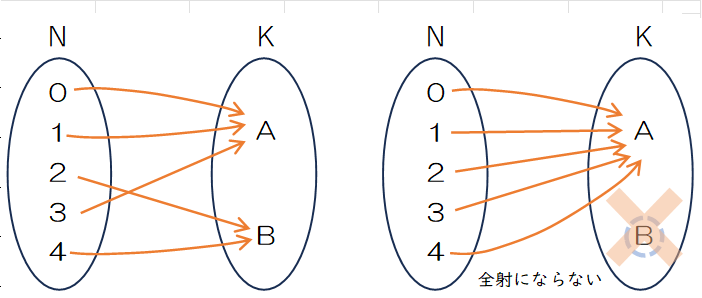
このことから、n=5, k=2のときの全射の重複順列の数は、全射・単射の制限がない任意の写像の $2^5=32$通りに対し、$(A, A, A, A, A)$、$(B, B, B, B, B)$ の 2通りが取り除かれ、30通りが全射の場合の数であることがわかりました。

全射の重複順列を抽出するプログラム

任意の写像から全射の写像を抽出

全射の重複順列を生成するため、ある写像が全射の要件を満たすかを判断する必要があります。そこで、全射の場合には単射とは異なり、写像だけではなく集合$K$の要素がないと判断できませんそこで、引数として、写像をseq、全射であるかの判断の基準となる集合$K$の要素をtargetとします。

Code 1.17　写像が全射の要件を満たすかを判断

def is_surjective(seq, target):
for idx in target:
if idx not in seq:
return False
return True
seq1 = (5, 3, 3, 4, 1, 3)
print(f'cycle of {seq1} = {is_surjective(seq1,(1,2,3))}')
seq2 = (5, 4, 2, 1, 3, 0)
print(f'cycle of {seq2} = {is_surjective(seq2,(1,2,3))}')

cycle of (5, 3, 3, 4, 1, 3) = False
cycle of (5, 4, 2, 1, 3, 0) = True

2.　すべてのtargetの要素は、数なくとも一つはseqの要素と対応している必要があります。このため、taegtの要素をidxとして順次読み込みます。

3.　idx not in seqはidxがシーケンスseqの中に存在しなければTrueが返されます。

4.　3.がTrueになったときは全射ではなくなるのでFalseを返します。

5.　targetの全ての要素でseqとの対応が見られた場合、2行目のループから抜けるのでTrueを返します。

さっそく、is_surjective関数を使い抽出します。

Code 1.18　重複順列から全射の写像を抽出

k_list= ['A', 'B']
n = 5
arbitrary_perm_list = generate_arbitrary_perm(k_list, n)
surjective_list_from_arbitrary = []
for perm in arbitrary_perm_list:
if is_surjective(perm, k_list ):
surjective_list_from_arbitrary.append(perm)
surjective_list_from_arbitrary
print(
f'arbitrary_perm_list({len(k_list)}, {n}) :'
f'count = {len(arbitrary_perm_list)}'
)
print(
f'surjective_list_from_arbitrary({len(k_list)}, {n}) :'
f' count = {len(surjective_list_from_arbitrary)}'
)

arbitrary_perm_list(2, 5) :count = 32
surjective_list_from_arbitrary(2, 5) : count = 30

4.　 generate_arbitrary_perm関数を使い重複順列を生成し、結果をarbitrary_perm_listに代入します。

7.　 is_surjective関数を使い、全射の要件を満たす写像のみをinjective_listに追加します。

この例では、全射の条件を満たしているかは最後の 1 人にならないと判断できないので、 item を elm に追加するところを n-1 とそれ以前に分けて、最後の 1 人で全射かどうかを判断します。

この原理を使い、全射の重複分割を生成する関数を作成します。さっそく、is_surjective関数を使い抽出します。

Code 1.18では、重複順列をすべて作ってから全射のものを絞り込んでいましたが、ここでは、n-1 個目までは制限なしにリストを生成し、重複分割を生成し、最後の 1 つで全射の要件を満たさない写像のみを追加するようにします。このことにより少しではありますが、効率よく処理することが期待されます。

全射の重複順列を直接生成する関数

これまでの結果から、全射の重複順列を直接生成する関数を作成します。

Code 1.19　全射の重複分割を生成

def generate_surjective_perm(k_list, n):
perm_list = [()]
for _ in range(n - 1):
next_perm = []
for elm in perm_list:
for item in k_list:
next_perm.append(elm + (item,))
perm_list = next_perm
result = []
for elm in perm_list:
for item in k_list:
if is_surjective(new_elm := elm + (item,), k_list):
result.append(new_elm)
return result
perm_surjective_list = (
generate_surjective_perm(k_list, n)
)
if (
surjective_list_from_arbitrary
== perm_surjective_list
):
print(
f'surjective_list_from_arbitrary'
f'== perm_surjective_list'
)

surjective_list_from_arbitrary== perm_surjective_list

3.　n-1 個までは重複順列を同じように無条件にリストに追加します。

9.　最終的に戻り値にするリストを result として初期化します。

10. 最後のn個めは、is_surjective関数を使い全射の写像のみを result に追加します。

2つの結果は一致し、場合の数も30通りと一致し正しく作成できていることが確認できました。

上記のプログラムは、最後 1 つの要素を追加する際に全射か否かを判断する is_surjective関数を適用し、全射の写像を抽出しました。この方法は単純ではありますが、最後の最後で全射でない写像を切り捨てるので、n が大きくなると記憶を多く消費します。次に、改善したプログラムを作成します。

写像を作成する過程で、この後全射の要件を満たすことができないことがあきあらかな作成過程も最後まで残ってしまうので、効率の面で課題が残ります。

全射の重複順列を集合で考える

Example 1.4 (1)のように $k=2$ であれば、簡単に計算することができますが、数が増えるにしたがって計算が格段に複雑になります。そこで、 $k$ の数を 2,3,4 と増やしていきながら集合の考え方に沿って全射の重複順列の個数を計算し、最終的に $k$ がどんなに大きくなっても対応できるよう一般化します。

要素が2 つの集合の演算

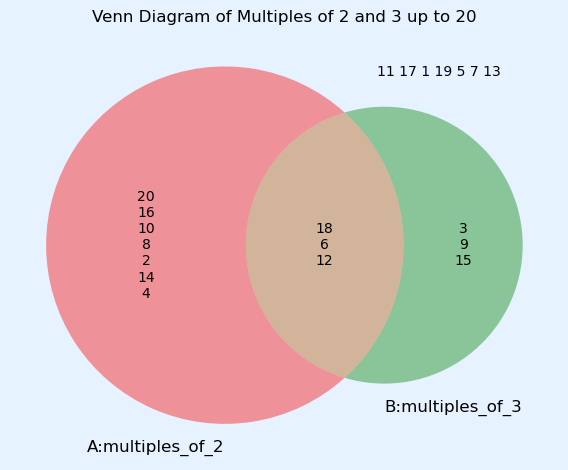
全体集合 U として 1 から 20 までの整数を定義します。次に 2 つの集合を定義します。

2 の倍数：集合 $A=\{2, 4, 6, 8,10, 12, 14, 16, 18, 20\}$ の 10 個

3 の倍数：集合 $B=\{3, 6, 9, 12, 15, 18\}$ の 6 個

これらの集合から、2 つの集合についての集合演算を行います。

集合 A と集合 B の共通部分は積集合（intersection)と呼び、 $A \cap B=\{6, 12, 18\}$ の 3 個になります。6 の倍数なので簡単に求めることができます。
集合 A か集合 B のいずれかに含まれている要素は和集合（union）呼び、$A \cup B=\{2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20\}$ の 13 個になります。
集合 A ではない要素は、集合の補集合（complement）と呼び、$\overline{A}$ と表記します。
集合 A には含まれるが集合 B に含まれない要素の集合を差集合（difference)と呼び $A-B=A\setminus B=A\cap \overline{B}=\{2, 4 , 8, 10, 14, 16, 20\}$ の 7 個になります。同様に $B-A=B\setminus A=B\cap \overline{A}=\{3, 9, 15\}$ の 3 個になります。また$ \overline{A} =U\setminus A$ となります。
A でも B でもない集合は、全体集合 U の補集合と呼び、$\overline{A \cup B }=U\setminus (A \cup B)=\{1, 5, 7, 11, 13, 17, 19\}$ の 7 個となります。

操作	英語	演算子	演算子	内包的記法
和集合	union	\|	$A\cup B$	$\{x \mid x \in A \vee x \in B\}$
積集合	intersection	&	$A\cap B$	$\{x \mid x \in A \wedge x \in B\}$
差集合	difference	-	$A\setminus B$	$\{x \mid x \in A \wedge x \notin B\}$
補集合	(complement)		$ \overline A$または $U \setminus A$	$\{ x \mid x \in U \land x \notin A \}$

Pythonによる集演演算とベン図の描画

Python による集合演算

Python を使って集合演算を行う際、Python では表の3 列目にある演算子を使うと、それぞれの集合演算をすることができます。

Code 1.20　2 つの集合の演算

n = 20
U = set(range(1, n + 1))
A = set(range(2, n + 1, 2))
B = set(range(3, n + 1, 3))
union = A | B
intersection = A & B
difference_AB = A - B
difference_BA = B - A
complement = (U - (A | B))
print(f'A | B = {union}')
print(f'A & B = {intersection}')
print(f'A - B = {difference_AB}')
print(f'B - A = {difference_BA}')
print(f'U - (A | B)= {complement}')

A | B = {2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20}
A & B = {18, 12, 6}
A - B = {2, 4, 8, 10, 14, 16, 20}
B - A = {9, 3, 15}
U - (A | B)= {1, 5, 7, 11, 13, 17, 19}

2.　整数を要素とする集合を定義するため、range関数で範囲を定めset関数で集合に変換します。

3.　集合Aは2の倍数2の倍数の集合を定義するため、range関数で(2,n+1,2)とすることにより、2から始まり2つおきに整数を設定することができます。

4.　集合Bは3から始まり3つおきの整数としてset(range(3, n + 1, 3))と定義します。

2つの集合のベン図

集合の関係を視覚的に理解するには、ベン図（Venn diagram）視覚的に理解しやすくなります。

集合の関係は、ベン図（Venn diagram）を用いることでベン図は、Pythonのグラフ描画ライブラリである matplotlib に依存する独立したベン図描画専用のパッケージである matplotlib-venn を使用することで描画できますこのうちvenn2 関数は、2つの集合のベン図を描画する関数として提供されています。

Code 1.21　2つの集合のベン図を描く

from matplotlib import pyplot as plt
from matplotlib_venn import venn2
fig, ax = plt.subplots()
diagram2 = venn2(
[A, B],
set_labels=('A: multiples_of_2', 'B: multiples_of_3')
)
plt.title('Venn Diagram of Multiples of 2 and 3 up to 20')
diagram2.get_label_by_id('10').set_text(
'\n'.join(map(str, difference_A_minus_B))
)
diagram2.get_label_by_id('01').set_text(
'\n'.join(map(str, difference_B_minus_A))
)
diagram2.get_label_by_id('11').set_text(
'\n'.join(map(str, intersection_AB))
)
plt.text(
0.6, 0.5,
' '.join(map(str, complement_AB)),
ha='right', va='top'
)
fig.patch.set_facecolor('#e6f2ff')
plt.tight_layout()
plt.show()
plt.show()

4.　venn2関数は 2 つの集合（$A$ と $B$）を引数として受け取り、ベン図を描画します。またset_labels パラメータで各集合の内容を説明するラベルを指定することができます。

6.　ベン図の各領域へのテキスト追加: get_label_by_id メソッドを使用して、ベン図の特定の領域にアクセスし、set_text で内容を設定しています。get_label_by_id メソッドの引数である10. ID は1桁目の1は1番目の集合Aの要素を表示するという意味です。同様に2桁目の0は2番目の集合Bの要素ではないことを示します。したがって、それぞれのIDは次の領域を表します。

　'10': $A$ のみの領域　 $A - B = \{2, 4, 8, 10, 14, 16, 20\}$

　'01': $B$ のみの領域　 $B - A = \{9, 3, 15\}$

　'11': $A$ と $B$ の共通部分 $A \cap B = \{18, 12, 6\}$

11. 10行目のset_texrメソッドは集合の要素を出力することはできないので、各要素にmap関数を使い、各要素に str関数を適用して文字列を要素とする map オブジェクトに変換したのち文字列'\n'に対して join メソッドの引数に指定します。Join メソッドはイテラブルを引数として取ることができます。なお、’\n ’は改行を表す特殊文字で、要素を横に並べるために使用しています。

19. venn2 には補集合を出力する機能がないので、注釈のようにテキストとして表示します。

$U - (A | B)= \{1, 5, 7, 11, 13, 17, 19\}$

plt.text(x, y, ' '.text, ha='right', va='top')において

x はテキストの表示場所の水平方向の位置を示します。グラフはおおむね-0.8 から 0.8 の範囲で描画されていますが、その中での座標を示します。Ha は horizontal alignment（水平方向の配置）の略で、right とした場合、文字列の右端が 0.6 の場所に来ることをしめしています。

同様に、垂直方向は y が-0.5 から 0.5 の範囲の中での表示位置を示します。

Va は vertical alignment（垂直方向の配置）の略で top とした場合、文字列は 0.5 を上端として表示することを示します。

なお、グラフの表示位置はplt.xlim(-1, 1)plt.ylim(-1, 1)

のように明示的に示すこともできます。なお、集合（set）の場合、要素が昇順に並ぶとは限らないので注意が必要です。

和集合と補集合の個数の計算

包除原理

全体集合$U$は、$A \cap \overline{B}$、$B \cap \overline{A}$、$A \cap B$,$ U\cap(\overline{A \cup B})$の4つの部分集合に分けることができます。この4つの部分集合は全体集合$U$は

要素 $x$ が $U$ の任意の要素である場合、 $x$ は必ずこれら 4 つの集合のいずれか 1 つだけに属することになり

互いに素（重なりがない） pairwise disjoint
すべてを合わせると全体集合 $U$ になる collectively exhaustive"

となり、全体集合 U の完全な分割（partition）といわれています。

これに対して、集合の要素の数を$n(U)$、集合 $A$、集合 $B$ の要素数は $n(A)$、$n(B)$、また$A \cap B$の要素数は$n(A \cap B)$と表記します。

このため次の式が成り立ちます。

$n({A \cup B})=n(A \cap \overline{B})+n(B \cap \overline{A})+n({A \cap B})=n(A)+n(B)-n({A \cap B})$

この式を包除原理といいます。また包除原理から

$n(\overline{A \cup B})=n(U)-n(A)-n(B)+n({A \cap B})$

となります。

\begin{align*}

n(\overline{A\cup B}) &= n(U) - n(A \cup B) && \text{補集合の性質} \\

\end{align*}

Equation 1.3　包除原理

\begin{align*}

n(\overline{A\cup B}) &= n(U) - n(A \cup B) && \text{complement} \\

&= n(U) - \{n(A) + n(B) - n(A \cap B)\} && \text{PIE} \\

&= n(U) - n(A) - n(B)\} + n(A \cap B) && \text{括弧の展開}

\end{align*}

このように $n(A \cup B)$ を計算する方法を包除原理（principle of inclusion and exclusion）、または頭文字をとってPIE（パイ /paɪ/）と呼びます。それでは包除原理を確認します。

Code 1.22　和集合、和集合の補集合の要素の個数

print(f'n(A | B)={len(A|B)}')
print(f'n(A)+n(B)-n(A & B)={len(A)+len(B)-len(A&B)}')
print(f'n(U)-n(A & B)={len(U-(A|B))}')

n(A | B)=13
n(A)+n(B)-n(A & B)=13
n(U)-n(A & B)=7

1.　$n(A \cup B)$を計算すると13個となり正しく計算することができました。

2.　$n(A)+n(B)-n(A \cap B)=10+6-3=13$となり、1.と一致することがわかります。

3.　全体集合の個数n(U)=20と$n(A \cup B)$の差が7となり、正しく計算できたことがわかります。

写像による計算との比較

全射の重複順列の個数を計算します。はじめに全体集合$U$は$2^5=32$になります。これに対してAが空室になる事象を集合Aとし、(B, B, B, B, B)が当てはまります。また、Bが空室になる事象を集合$B$とし、(A, A, A, A, A)が当てはまります。そこで、AもBも空室になることはありえないもので$n(A\cap B) =\varnothing$となり、重複順列は$A \cup B=2$になります。したがって求める全射の重複順列は集合$A$でも集合$B$でもないものを数えればよいことになります。これは$\overline{A\cup B}$のようになり、個数は全体集合$U$の個数32から$A\cup B$の2個を差し引いた30個になります。

このように集合論からアプローチしても計算結果が合致することがわかりました。

3つの集合の演算

３つの集合の写像

写像からみた包除原理

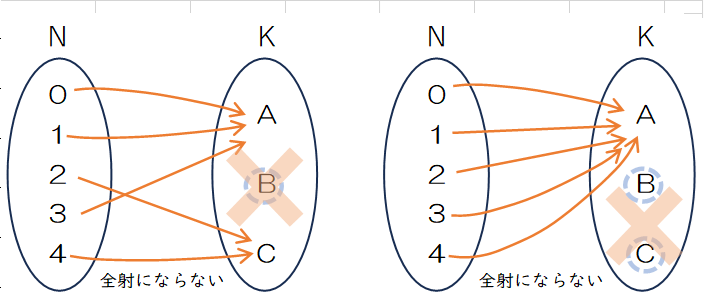
集合Kの要素が3つになると、話がむつかしくなります。例として、$n=\{0, 1, 2, 3, 4\}$、$k=\{A, B, C\}$ としてリストを作成します。

図の左のような(A, A, C, A, C)のようにBが選ばれない重複順列はもとより右のように(A, A, A, A, A)は全射になりません。

generate_surjective_perm関数を使い、重複順列を生成したのち個数を数え、任意の写像の重複縦列と比べます。

全射ではない写像では、定義域対応していない終域の要素が存在します。このような要素を未対応要素（non-attained element）と呼び、その数を未対応要素数（defect）と呼びます。そので、未対応要素数defectをキーワードに包除原理による場合の数を計算します。

①全体集合

空室も許した制約なしの重複順列$k^n$を計算します。全体集合Uは5人が3部屋を自由に選ぶことができるので$3^5=243$通りになります。

②1部屋以上空き部屋になる場合（defect）

Aが空き部屋になる集合Aの場合の数は5人をB, Cの部屋に割り振ることになるので、$2^5=32$通りになります。同じように、集合Bも集合Cも32通りになります。そこで空室が出ない重複順列は、全体集合からこれらA, B, Cの3つの集合の数の合計($32\times3=96$)を差し引くことで計算することができます。

③2部屋以上空き部屋になる場合

②で差し引いた中には (C, C, C)のように集合Aにも集合Bにも含まれる$n(A\cap B)$があり、その場合の数は$1^5=1$になります。$n(A\cap B)$は②で2重に差し引かれているので、逆に足し戻してやる必要があります。このようなものは$n(B\cap C)$である(A, A, A), $n(C\cap A)$である(B, B, B)の３つあります。

④3部屋以上空き部屋になる場合

集合の考え方からすると、ＡもＢもＣも空室の場合、$A\cap B\cap C$があれば、③で足し戻し過ぎになるので、さらに差し引く必要が生じます。もっとも今回は、全室空室はありえませんからここは0になります。

プログラムでの確認

上記の結果とgenerate_surjective_permの計算結果を比較します。

Code 1.23　K=3の場合の全射の計算

n = 5
k_list= ['A', 'B', 'C']
perm_surjective_list = generate_surjective_perm(k_list, n)
print(
f'generate_arbitrary_perm({len(k_list)}, {n}) = {len(k_list)**n} '
)
print(
f'generate_surjective_perm ({len(k_list)}, {n}) = {len(perm_surjective_list)}'
)
perm_surjective_list

generate_arbitrary_perm(3, 5) = 243 
generate_surjective_perm  (3, 5) = 150
[('A', 'A', 'A', 'B', 'C'),
 ('A', 'A', 'A', 'C', 'B'),
 ('A', 'A', 'B', 'A', 'C'),
 ('A', 'A', 'B', 'B', 'C'),
 ('A', 'A', 'B', 'C', 'A'),
 ('A', 'A', 'B', 'C', 'B'),
（中略）
('C', 'C', 'C', 'C', 'C'),

2.　perm_surjective_func関数で計算した結果を、リスト perm_surjective_list に代入します。

3.　重複順列 $3^5=243$通りのうち、全射は 150通りになります。この差の分析をして、個数の計算方法を考えます。

3つの集合の演算

集合演算の考え方

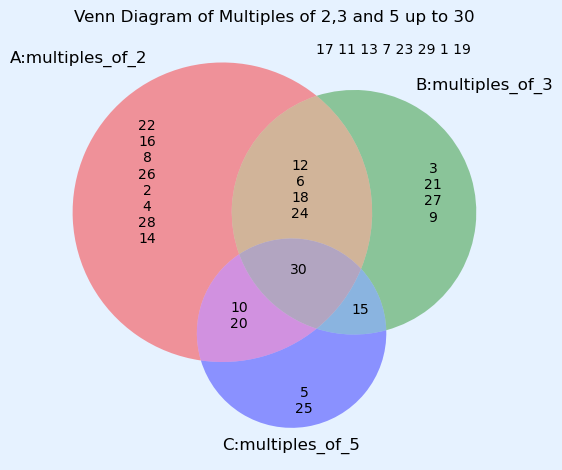
全体集合$U$として1から30までの整数を定義します。これに対して、

2の倍数の集合$A=\{2, 4, 6, 8,10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30\}$の15個、

3の倍数の集合$B=\{3, 6, 9, 12, 15, 18, 21, 24, 27, 30\}$の10個、

5の倍数の集合$C=\{5, 10, 15, 20, 25, 30\}$の5個

とします。

これに対して、次の積集合は簡単に計算ることができます。

6の倍数の集合$A\cap B=\{6, 12, 18, 24, 30\}$

15の倍数の集合$B\cap C=\{15, 30\}$

10の倍数の集合$C\cap A=\{10, 20, 30\}$

30の倍数の集合$A\cap B\cap C=\{30\}$

ここから完全な分割を

集合$A$集合$B$集合$C$の共通部分（intersection) $A \cap B=\{30\}$の1個になります。30の倍数なので簡単に求めることができます。

次に3つの集合の場合の複雑な例として集合$A$、集合$B$の要素ではあるが集合$C$の要素ではないような集合が考えられます。特にきまった名称はありませんが、ここではAとBの「A,Bの積集合からCを除いた部分」と呼ぶことにします。このようなケースは次の3つが考えられます。

A,Bの積集合からCを除いた部分　$A \cap B \cap \overline{C}=\{6, 12, 18, 24\}$

AとCの積集合からBを除いた部分$A \cap C \cap \overline{B}=\{10, 20\}$

BとCの積集合からAを除いた部分$B \cap C \cap \overline{A}=\{15\}$

さらに集合$A$には含まれるが、その他の集合には含まれないような集合を相対的補集合(relative_complement)といいます。このような集合も次の3つのケースがあります。

$A \cap\overline{B}\cap\overline{C}=A \setminus B \setminus C=\{2, 4, 8, 14, 16, 22, 26, 28\}$

$B \cap\overline{A}\cap\overline{C}=B \setminus A \setminus C=\{3, 9, 21, 27\}$

$C \cap\overline{A}\cap\overline{B}=C \setminus A \setminus B=\{5, 25\}$

プログラムで確認

これらの演算を行うと次のようになります。

Code 1.24　 3つの集合間の関係を分析

n = 30
U = set(range(1, n + 1))
A = set(range(2, n + 1, 2))
B = set(range(3, n + 1, 3))
C = set(range(5, n + 1, 5))
union_ABC = A | B | C
intersection_ABC = A & B & C
intersection_AB_minus_C = A & B - C
intersection_BC_minus_A = B & C - A
intersection_AC_minus_B = A & C - B
difference_A_minus_BC = A - B - C
difference_B_minus_AC = B - A - C
difference_C_minus_AB = C - A - B
complement_ABC = (U - (A | B | C))
print(f'A | B | C ={union_ABC}')
print(f'A & B & C = {intersection_ABC}')
print(f'A & B - C = {intersection_AB_minus_C}')
print(f'B & C - A = {intersection_BC_minus_A}')
print(f'A & C - B = {intersection_AC_minus_B}')
print(f'A - (B | C) = {difference_A_minus_BC}')
print(f'B - (A | C) = {difference_B_minus_AC}')
print(f'C - (A | B) = {difference_C_minus_AB}')
print(f'U - (A | B | C) = {complement_ABC}')

A | B | C ={2, 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30}
A & B & C = {30}
A & B - C = {24, 18, 12, 6}
B & C - A = {15}
A & C - B = {10, 20}
A - (B | C) = {2, 4, 8, 14, 16, 22, 26, 28}
B - (A | C) = {27, 9, 3, 21}
C - (A | B) = {25, 5}
U - (A | B | C) = {1, 7, 11, 13, 17, 19, 23, 29}

2.　全体集合として1からn =30までの整数を集合Uとして定義します。定義するときはrangeで定義した範囲にset関数を適用します。同様に2から5で次の通り集合を定義します。

U: 1から30までのすべての整数

A: 2の倍数（2, 4, 6, ..., 30）

B: 3の倍数（3, 6, 9, ..., 30）

C: 5の倍数（5, 10, 15, ..., 30）

6.　積集合の演算子を使って、A,B,Cの積集合を計算します。変数名はintersection_ABCとします。

7.　積と差集合の演算子を使い「積集合からCを除いた部分」を計算します。変数名はintersection_AB_minus_C とします。同様に、Bを除いた部分、Aを除いた部分を計算します。 = A & B & C intersection_AB_minus_C = A & B - C intersection_BC_minus_A = B & C - A intersection_AC_minus_B = A & C - B 集合の交差と差集合を計算しています。&演算子は交差を、-演算子は差集合を表します。

11.　 AではあるがBでもCでもない集合、変数をdifference_A_minus_BC = A - B - Cとします。ここでは$A \setminus (B \cup C)$の式で計算していますが、次の式でも計算することができます。

14.　complement = (U - (A | B | C)) 全体集合Uに対するA, B, Cの和集合の補集合を計算しています。

15.　print(f'A & B & C = {intersection_ABC}')

3つの集合のベン図

3つの集合の関係を見るためにベン図を描いてみます。

Code 1.25　venn3による3つの集合のベン図を描く

from matplotlib import pyplot as plt
from matplotlib_venn import venn3
fig, ax = plt.subplots()
diagram3 = venn3(
[A, B, C],
set_labels=(
'A: multiples_of_2',
'B: multiples_of_3',
'C: multiples_of_5'
)
)
plt.title('Venn Diagram of Multiples of 2, 3 and 5 up to 30')
diagram3.get_label_by_id("100").set_text(
'\n'.join(map(str, difference_A_minus_BC))
)
diagram3.get_label_by_id("010").set_text(
'\n'.join(map(str, difference_B_minus_AC))
)
diagram3.get_label_by_id("001").set_text(
'\n'.join(map(str, difference_C_minus_AB))
)
diagram3.get_label_by_id("110").set_text(
'\n'.join(map(str, intersection_AB_minus_C))
)
diagram3.get_label_by_id("011").set_text(
'\n'.join(map(str, intersection_BC_minus_A))
)
diagram3.get_label_by_id("101").set_text(
'\n'.join(map(str, intersection_AC_minus_B))
)
diagram3.get_label_by_id("111").set_text(
'\n'.join(map(str, intersection_ABC))
)
plt.text(
0.6, 0.6,
' '.join(map(str, U - (A | B | C))),
ha='right', va='top'
)
fig.set_facecolor('#e6f2ff')
plt.tight_layout()
plt.show()

2.　Matplotlib（グラフ描画ライブラリ）の拡張ライブラリをインポートします。

6.　diagram3.get_label_by_id("xxx").set_text("\n".join(yyy)) get_label_by_id メソッドを使用して、ベン図の特定の領域にアクセスし、set_text で内容を設定しています。"xxx" の部分は

"100":$A \cap\overline{B}\cap\overline{C}=A \setminus B \setminus C=\{2, 4, 8, 14, 16, 22, 26, 28\}$

"010": $\overline{A}\cap B \cap\overline{C}=B \setminus A \setminus C=\{3, 9, 21, 27\}$

"001": $\overline{A}\cap\overline{B} \cap C =C \setminus A \setminus B=\{5, 25\}$

"110": A,Bの積集合からCを除いた部分　$A \cap B \cap \overline{C}=\{6, 12, 18, 12, 24\}$

"011": AとCの積集合からBを除いた部分$A \cap C \cap \overline{B}=\{10, 20\}$

"101": BとCの積集合からAを除いた部分$B \cap C \cap \overline{A}=\{15\}$

"111": A, B, C の共通部分テキストは '\n'.join() を使用して複数の要素を改行で区切って表示し

plt.show() 作成したベン図を表示します。

この計算から、3つの集合の包除原理は次の式になります。

3つの要素の集合での集合演算

ここで計算した包除原理をkが増えても対応できるように、一般化します。このときに、k=2の包除原理の公式に次の法則を適用してk=3の公式にします。

集合演算

3つの集合の積集合、和集合を3つ以上つなげた場合は、計算する順序によらず同じ結果になります。

Equation 1.4　結合法則 associative property

$A \cup B \cup C=(A \cup B) \cup C=A \cup(B \cup C)$

$A \cap B \cap C=(A \cap B) \cap C=A \cap(B \cap C)$

この法則は、ベン図を見れば明らからで、今後の計算で適用できるものとして考えます。ただし、結合法則が成り立つのは、和集合、積集合が同じ記号が並んだ時だけです。記号が混在するときには、次の分配法則が成り立ちます。

和集合と積集合が混在する場合は次のような法則が成り立ちます。

Equation 1.5　分配法則 distributive law

$A \cup(B \cap C)=(A \cup B) \cap(A \cup C)$

$A \cap(B \cup C)=(A \cap B) \cup(A \cap C)$

$(A \cap B) \cup C=(A \cup C) \cap(B \cup C)$

$(A \cup B) \cap C=(A \cap C) \cup(B \cap C)$

また、当たり前のようですが、冪等法則も注意が必要です。冪等法則は和集合と積集合についての法則がありますが、ここでは積集合の冪等法則を使います。

また、これも当然ですが、つぎのような法則も演算に必要になります。

Equation 1.6　交換法則　commutative law

$A \cup B = B \cup A$

$A \cap B = B \cap A$

当然ですが次の法則もあります。

Equation 1.7　冪等法則　Idempotency of Union

$A \cup A =A$

$A \cap A =A$

ここでは結合法則と積集合の冪等法則と交換法則を使って次のような変形が必要になります。A,Bの2つの包除原理にＣを追加することで発展させていきます。

$(A \cap C) \cap (B \cap C) = A \cap B \cap C$

ここから、集合の数が3の場合の方除原理の計算は次の通りになります。

\begin{align*} n(A \cup B \cup C)&= n((A \cup B) \cup C))) && \text{結合法則} \\ &= n(A \cup B) +n(C) - n((A\cup B) \cap C)) && \text{包除原理} \\ \end{align*}

ここで$n(A \cup B)$については、k=2の包除原理を使うことができます。$n((A\cup B) \cap C))$については次の通り展開します。

\begin{align*} n((A\cup B) \cap C))&= n(A \cap C) \cup (B \cap C )) && \text{分配法則} \\ &= n(A \cap C) +n(B \cap C)-n((A \cap C) \cap (B \cap C )) && \text{包除原理} \\ &= n(A \cap C) +n(B \cap C)-n(A \cap B \cap C) && \text{以下参照} \\ \end{align*}

このうち$n((A \cap C) \cap (B \cap C ))$については

\begin{align*} n((A \cap C) \cap (B \cap C ))&=n(A \cap C \cap B \cap C ) && \text{結合法則} \\ &=n(A \cap B \cap C \cap C )&& \text{交換法則} \\ &=n(A \cap B \cap C)&& \text{冪等法則} \\ \end{align*}

となります。

まとめると次の通りになります。

\begin{align*} n(A \cup B \cup C)&= n((A \cup B) \cup C))) \\ &= n(A \cup B) +n(C) - n((A\cup B) \cap C)) \\ &= n(A)+n(B)- n(A \cap B)+n(C)\\ &-\{n(A \cap C) +n(B \cap C)-n(A \cap B \cap C )\} \\ &= n(A)+n(B)+n(C) \\ &-n(A \cap B)-n(A \cap C) -n(B \cap C) \\ &+n(A \cap B \cap C ) \\ \end{align*}

次のことがいえます。集合が同時に交わる箇所の数集合の結合の個数（交わりの次数としますDegree of Intersection）ごとに整理します。

deg=1

n(A),n(B),n(C)は1の合計になります。

deg=2

A,BおよびCの3つの要素から2つを選んだ組み合わせはA,Bの組み合わせとA,BとCの組み合わせになります。

deg=3

2の中でA,B,Cの3つの積になります。

\begin{align*} n(\overline{A \cup B \cup C}) &= n(U) - n(A \cup B \cup C) \\ &= n(U) - n(A) - n(B) - n(C) \\ &\quad + n(A \cap B) + n(A \cap C) + n(B \cap C) \\ &\quad - n(A \cap B \cap C) \end{align*}

これは、ベン図を見ればよくわかります。

Equation 1.8　3つの集合の包除原理

$ n(A \cup B \cup C)$

$= n(A)+n(B)+n(C)- n(A \cap B) -n(A \cap C) -n(B \cap C)+n(A \cap B \cap C)$

$n(\overline{A\cup B \cup C})=n(U)-n(A \cup B \cup C)$

$=n(U)-n(A)-n(B)-n(C)+ n(A \cap B) +n(A \cap C) +n(B \cap C)-n(A \cap B \cap C)$

ベン図を課題に適用する

計算式は次の通りになります。

Equation 1.9　n=5,k=3のときの全射の重複順列の個数

$n(\overline{A\cup B\cup C})$

$=n(U)-\{n(A)+n(B)+n(C)\}$

$+\{n(A\cap B)+n(B\cap C)+n(C\cap A)\}-n(A\cap B\cap C)$

$=243-32\times3+1\times3-0=150$

4つの集合の演算から一般化する

写像で4つの集合の全射の重複順列を表記

k=4の全射の重複順列を写像から計算する

k=4ともなると、matplotlibライブラリにも描くためのサブパッケージもなく、そもそも複雑すぎてベン図では対応できません。こんなときは写像の出番です。①で重複順列を計算し、②から④で全射の要件を満たさない重複順列を加減します

①全体集合

空室を許容する制約なし写像である重複順列$k^n$を計算します。全体集合Uは7人を4部屋に割り振る重複順列になるので$4^7=16384$通りになります。

②1部屋以上空き部屋になる場合

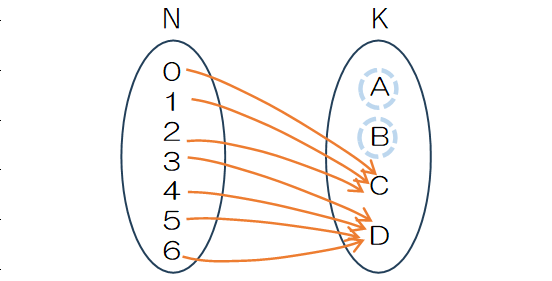
1部屋以上が空きになるのは、図の左側のようにAが空きになるケースや、右のようにBが空きになるケースが考えられます。このほか、当然C,Dが空き部屋になる場合もあるので合計4ケースになります。

この4つのケースのうち1つ、図の左側のように7人をB, C, Dの3部屋に割り振るので、$3^7=2187$通りになります。同じように、集合B、C、Dも2187通りになるので、空室が出ない重複順列は全体集合 ($2187\times4=8748$)を差し引くことで計算することができます。

③2部屋以上が空きになる重複順列を足し戻す

図のようにAもBも空き部屋になる$A\cap B$のようなケースでは、①では1でカウントされていますが、②ではAとBでも二重に差し引かれてしまいます。この不都合を解消するために、いったん差し引いたものを足し戻す必要があります。同様に$A\cap C, A\cap D,B\cap C, B\cap D, C\cap D $を合わせて6ケース、つまり4つの部屋から2つを選ぶので${}_4 C_2 $通りとなります。

その6ケースのうち1つ、$A\cap B$では C,Dの2部屋に7人が泊まることになるので$2^7=128$通りとなります。このため、6ケース×128=768通りを足し戻す必要があります。

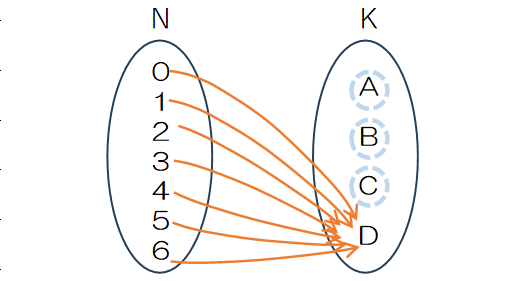
④3部屋以上が空きになる重複順列を再び差し引く

図のようにAもBもCも空き部屋$A\cap B\cap C$では③で重複して「足し戻し過ぎ」の状態にあるので、再び差し引く必要があります。

同様に$A\cap B\cap D, A\cap C\cap D, B\cap C\cap D $を合わせて4ケース、つまり4つの部屋から3つを選ぶので${}_4 C_3 $通りとなります。

その4ケースのうち1つ、$A\cap B\cap C$では Dの1部屋に7人が泊まることになるので$1^7=1$通りとなります。このため、4ケース×1=4通りを再び差し引く必要があります。

⑤4部屋以上が空きになる重複順列があれば差し引く

もし、AもBもCもDも空き部屋という重複順列があれば、引きすぎたものを再度足し戻す必要があります。もっともn=4の場合は0になるので、考える必要はありません。

重複順列$4^5=16384$通りのうち、全射のものは8400通りになります。

まとめると次のようになります。

$n(U)=4^7=16384$

$n(A)=n(B)=n(C)=n(D)=3^7=2187$

$n(A\cap B)=n(A\cap C)=n(A\cap D)=n(B\cap C)=n(B\cap D)=n(C\cap D)=2^7=128$

$n(A\cap B\cap C)=n(A\cap B\cap D)=n(A\cap C\cap D)=n(B\cap C\cap D)=1^7=1$

$n(A\cap B\cap C\cap D)=0^7=0$

$n(A \cup B \cup C \cup D)=2187\times4-128\times 6+1\times 4-0=7984$

$n(\overline{A\cup B\cup C\cup D})=n(U)-n(A \cup B \cup C \cup D)=16384-7984=8400$

関数による計算

k=4になると、さらに複雑になります。kがさらに増えることも見据えて検討します。組合せと件数を確認します。ここではn=7、k_list= ['A', 'B', 'C', 'D']とします。

Code 1.26　４部屋の場合

n = 7
k_list= ['A', 'B', 'C', 'D']
perm_surjective_list = generate_surjective_perm (k_list, n)
print('arbitrary = ',len(k_list)**n,'surjection = ',len(perm_surjective_list))
pprint.pprint(perm_surjective_list)

arbitrary =  16384 surjection =  8400
[('A', 'A', 'A', 'A', 'B', 'C', 'D'),
 ('A', 'A', 'A', 'A', 'B', 'D', 'C'),
 ('A', 'A', 'A', 'A', 'C', 'B', 'D'),
 ('A', 'A', 'A', 'A', 'C', 'D', 'B'),
  ・
・
('D', 'D', 'D', 'D', 'C', 'B', 'A')]

全射の場合の数の計算

n=4にもなると何度も加減を繰り返すので、本当に正しく計算されているか不安になります。そこで、全射の条件を満たさない2例について最終的に差し引かれるまでの流れを整理します。

(D, D, D, D, D, D, D)のようなに集合A,B,Cに当てはまるケース

①では制約なしの全体集合を計算しているので1でカウントされていますが、全射の条件を満たしていないの②～④の計算の結果、最終的に0に落ち着かせることが必要になります。

②では集合A,B,Cとして3回（${}_3 C_1 $）差し引かれています。

③では$A\cap B$、$A\cap C$と$B\cap C$の3回（${}_3 C_2 $）で足し戻されています。

④では$A\cap B\cap C$（${}_3 C_3 $）で1回、再度差し引かれます。

よって1-3+3-1=0となり思った通りの結果になります。

ここで①は常に1なので${}_3 C_0$と考えることができます。ところで、${}_3 C_0 – {}_3 C_1+ {}_3 C_2 – {}_3 C_3 =1-3+3-1=0$となるのでうまく計算できたことがわかります。

(C, D, D, D, D, D, D)のようなに集合A,Bに当てはまるケース

では制約なしの全体集合を計算しているので1でカウントされています。

②では、A,Bとして2回（${}_2 C_1 $）差し引かれています。

では、$A\cap B$として足し戻されます。

結果${}_2 C_0 – {}_2 C_1+ {}_2 C_2=1-2+2=0$となりやはり正しく計算されています。

この考え方を拡張するとkがもっと大きくなっても、空き部屋の数を、差し引く集合の重複数をiとすると、最終的に重複順列としてカウントされるのは、次の式で計算することができます。

$\sum\limits_{i=0}^{x}(-1)^i\,{}_xC_i={}_x C_0 –{}_x C_1+{}_x C_2-{}_x C_3+\cdots \pm{}_x C_x$

この式の値は$(1-x)^n$を二項定理にあてはめて展開し、$x=1$を代入して計算することができます。ここで空き部屋の数をd（defect）とします。

$\displaystyle (1-x)^d=\sum_{i=0}^{d} {}_dC_i x^i={}_dC_0x^0-{}_dC_1x^1+{}_d C_2x^2-{}_dC_3x^3+\cdots {}_d C _d x^d$

$x=1$を代入すると

$( 1-1)^d=\sum\limits_{i=0}^{d}{}_dC_i={}_dC_0-{}_dC_1+{}_dC_2-{}_dC_3+\cdots{}_dC_d=0$ $

(A, A, B, B, C, C, D)のようなにどの集合にも当てはまらない場合

この場合は空き部屋がでないので、最終的に1でカウントされます。これを式に当てはめると$0^0=_0C_0=0!/(0!\times0!)=1$となります。整数の0乗は1というのはわかるとして$0^0=1$というのは違和感を感じますが、この例を見ると確かに頷けます。

まとめると次のようになります。

Equation1.10　空き部屋がいくつでカウントされるか

$\sum\limits_{i=0}^{x}(-1)^i\,{}_{x}C_i={}_x C_0 –{}_x C_1+{}_x C_2-{}_x C_3+\cdots \pm{}_x C_x=0 $ただし$x=0$のときは1

集合演算による4つの集合の包除原理

3つの集合の包除原理の計算式を発展させ、$n(A \cup B \cup C \cup D)$を求めます。

この計算式は次の通り、結合法則、分配法則、和集合の冪等法則を繰り返し適用することにより求めることができます。

はじめに、包除原理により、次の通り分解することができます。

\begin{align*} n(A \cup B \cup C \cup D) &= n((A \cup B \cup C) \cup D) && \text{Associative Law} \\ &= n(A \cup B \cup C) + n(D) - n((A \cup B \cup C) \cap D) && \text{PIE} \\ &= n(A \cup B \cup C) + n(D) \\ &\quad - n((A \cap D) \cup (B \cap D) \cup (C \cap D)) && \text{Distributive Law} \end{align*}

このうち、

第1項は3つの集合の包除原理の計算式

第2項は$n(D)$

第3項は、A,BおよびCとDの積集合に包除原理を適用した数になり、次に通り展開することができます。

\begin{align*} &n((A \cap D) \cup (B \cap D) \cup (C \cap D)) \\ &= n(A \cap D) + n(B \cap D) + n(C \cap D) \\ &\quad - (n((A \cap D) \cap (B \cap D)) + n((A \cap D) \cap (C \cap D)) \\ &\quad\quad + n((B \cap D) \cap (C \cap D))) \\ &\quad + n((A \cap D) \cap (B \cap D) \cap (C \cap D)) \\ &= n(A \cap D) + n(B \cap D) + n(C \cap D) \\ &\quad - (n(A \cap B \cap D) + n(A \cap C \cap D) + n(B \cap C \cap D)) \\ &\quad + n(A \cap B \cap C \cap D) \end{align*}

この中で、$n((A \cap D) \cap (B \cap D)) = n(A \cap B \cap D)$は前項で確認しました。同様に最後の項は次の式により計算することができます。

\begin{align*} &n((A \cap D) \cap (B \cap D) \cap (C \cap D)) && \\ &= n(A \cap D \cap B \cap D \cap C \cap D) && \text{Associative Law} \\ &= n(A \cap B \cap C \cap D \cap D \cap D) && \text{Commutative Law} \\ &= n(A \cap B \cap C \cap D) && \text{Idempotent Law} \end{align*}

これらをすべて合わせると次のようになります。

\begin{align*} n(A \cup B \cup C \cup D) &= n(A) + n(B) + n(C) + n(D) \\ &\quad - [n(A \cap B) + n(A \cap C) + n(A \cap D) \\ &\quad\quad + n(B \cap C) + n(B \cap D) + n(C \cap D)] \\ &\quad + [n(A \cap B \cap C) + n(A \cap B \cap D) \\ &\quad\quad + n(A \cap C \cap D) + n(B \cap C \cap D)] \\ &\quad - n(A \cap B \cap C \cap D) \end{align*}

かなり複雑な数式になりますが、さらに集合の数が増えても対応する準備として、構造を整理します。

第1項は3つの集合の包除原理の計算式

第2項は$n(D)$

第3項はA,BおよびC

左式集合が同時に交わる箇所の数集合の結合の個数（交わりの次数としますDegree of Intersection）ごとに整理します。

deg=1

n(A),n(B),n(C)は1の合計になります。

deg=2

1でAとBのCのうち2つの積集合　積$n(A \cap B)$

2でA、BおよびCとDの積集合

ここで、2つを合わせると4つの集合から2つを選んだものになります。

この考え方は、組み合わせの有名な公式に当てはめるとよくわかります

$ {}_n C_r = {}_{n-1}C_r+{}_{n-1} C_{r-1}$

つまり、n人からr人選ぶときに、特定の人が選べれない組み合わせは${}_{n-1}C_r$、選ばれる組み合わせは${}_{n-1} C_{r-1}$の和になるというものです。この場合4つの集合に対してdeg=2なので${}_4 C_2=6$個に対して、集合Dが選ばれない場合、${}_3 C_2=3$、選ばれる場合${}_3 C_1=3$の3個になります。なお、degは１ではマイナス、２ではプラスになりますが、２マイナスのなのでいずれもマイナスになります。

deg=3

A,BおよびCの3つの要素から3つを選んだ組み合わせ、２ではA,BおよびCの3つの要素から2つを選んだ積集合とDの積集合となります。つまり、4つの集合から3つを選んだ4とおりになります。これも

積$n(A \cap C)$、$n(B \cap C)$を差し引いています。

A,BおよびCの3つの要素から2つを選んだ組み合わせはA,Bの組み合わせとA,BとCの組み合わせになります。${}_3 C_3+{}_3 C_2=4$となります。なお、符号については１はプラス、２はマイナスですが２自体がマイナスなのでプラスになります。

deg=4

2の中でA,B,C,Dの4つの積集合になります。

k	±	$n(A \cup B \cup C)$	$n(D) - n((A \cup B \cup C) \cap D)$
1	+	$n(A) + n(B) + n(C)$	$n(D)$
2	−	$n(A \cap B) + n(A \cap C) + n(B \cap C)$	$n((A \cap D) + (B \cap D) + (C \cap D))$
3	+	$n(A \cap B \cap C)$	$n(A \cap B \cap D) + n(A \cap C \cap D) + n(B \cap C \cap D)$
4	−		$n(A \cap B \cap C \cap D)$

最終的に次のようになります。

\begin{align*} n(\overline{A \cup B \cup C \cup D}) &= n(U) - n(A \cup B \cup C \cup D) \\ &= n(U) - n(A) - n(B) - n(C) - n(D) \\ &\quad + n(A \cap B) + n(A \cap C) + n(A \cap D) \\ &\quad + n(B \cap C) + n(B \cap D) + n(C \cap D) \\ &\quad - n(A \cap B \cap C) - n(A \cap B \cap D) \\ &\quad - n(A \cap C \cap D) - n(B \cap C \cap D) \\ &\quad + n(A \cap B \cap C \cap D) \end{align*}

Equation 1.11 　4つの集合の包除原理

$ n(A \cup B \cup C \cup D)$

$= n(A)+n(B)+n(C)+n(D)$

$-\{n(A \cap B)+n(A \cap C)+n(A \cap D)+n(B \cap C)+n(B \cap D)+n(C \cap D)\}$

$+\{n(A \cap B \cap C)+n(A \cap B \cap D)+n(A \cap C \cap D)+n(B \cap C \cap D)\}$

$-n(A \cap B \cap C \cap D)$

二項定理と重複順列の全射が思わぬところで結びつきました。

重複順列の全射の場合の数を計算する関数

最後に、全射の重複順列の場合の数の計算方法の一般化を試みます。部屋の数k=4に対して空き部屋の数をiとします。人数が6人なので、制約なしの場合、重複順列は$4^6$となります。

①の制約なしの場合、$k^n$となりますが、このとき空き部屋は0なのでi=0となります。これ以降の加減は表の通りになります。タイプには、代表的なものを示していますが、これを見ればそれぞれの組合せが${}_k C_i$であることがわかります。また、k=0のときに＋、これ以降は交互にプラスとマイナスを繰り返すので$(-1)^i$であらわします。

表を見ると数式は図の通りになります。

このような計算方法を包除原理（Inclusion-exclusion principle）といい、全射の計算で威力を発揮します。

これまで例で取り上げた重複順列を一般化すると次のようになります。

Equation 1.12　重複組合せの全射の個数

$\sum\limits_{i=0}^{k}(-1)^i {}_{k} C_i(k-i)^n=_{k} C_0k^n-_{k} C_1(k-1)^n+{}_{k} C_2(k-2)^n- \cdots\pm{}_{n} C_n(n-n)^n $

上記の計算式を使い、全射の重複順列の個数を計算する関数を作成します。関数名は順列の全射という意味で、perm_surjective_countとし、引数はこれまでと同じようにk,nとします。また、関数を使い、これまで検討した3ケースについて計算し検証します。

Code 1.27　全射の重複組合せの件数を計算

def perm_surjective_count(k, n):
sigma = 0
for i in range(k+1):
sigma += ((-1)**i) * comb(k,i) * (k-i)**n
return int(sigma)
print(f'surjective(2, 5):{perm_surjective_count(2, 5) :>5}')
print(f'surjective(3, 5):{perm_surjection_count(3, 5) :>5}')
print(f'surjective(4, 7):{perm_surjective_count(4, 7) :>5}')

surjective(2, 5):   30
surjective(3, 5):  150
surjective(4, 7): 8400

4.　数式を当てはめます。

これまでに3つの例を挙げて計算してきましたが、結果は合致していることがわかります。計算式は正しそうですが、さらに詳しい証明も欲しくなります。このあたりはまた別の機会に譲ります。

全射の要件を満たすことができなくなった時点で候補から外す

全射の重複分割を生成するにあたり、

例えばn=7,k=4で、5回目のループで()となった時点で、残り2回のループでBCDの3つをすべて選択することはできないので、全射の写像として完成させることができなくなります。このため、この時点でリストに追加しないようにします。

Code 1.28　制約をつけて全射の重複順列を生成

def generate_surjective_perm_with_constraint(k_list, n):
k = len(k_list)
perm_list = [()]
for i in range(n):
next_perm = []
for elm in perm_list:
for item in k_list:
new_elm = elm + (item,)
if k - len(set(new_elm)) <= n - i - 1:
next_perm.append(new_elm)
perm_list = next_perm
return perm_list
perm_surjective_with_constraint = (
generate_surjective_perm_with_constraint(k_list, n)
)
print(
f'perm_surjective_with_constraint({len(k_list)}, {n}) = '
f'{len(perm_surjective_list2)}'
)
if (
perm_surjective_list_by_filtering
== perm_surjective_with_constraint
):
print(
f'perm_surjective_list_by_filtering '
f'== perm_surjective_with_constraint'
)

perm_surjective_with_constraint(4, 7) = 8400
perm_surjective_list_by_filtering == perm_surjective_with_constraint

9.　 k - len(set(new_elm)は全射の要件を満たすために、何種類k_listから選べばよいかを示しています。一方n - i – 1は、あと何回ループを回すのか示しています。このため前者が後者以下の場合は全射の写像として完成させることができるので、候補としてnext_permに追加します。また、前者が後者より大きくなった時点で候補から外れるのでnext_permには追加しません。