全単射の順列、モンモール数

定義域Nと終域Kの要素の個数が等しい順列

重複順列、順列の仕上げとして全射と単射の両方の要件を満たす全単射の例を取り上げます。概要を把握するため、次の問題を考えます。

問題4

4人の学生が合宿でそれぞれ個室に泊まることとします。宿舎にはK={A, B, C, D}の4部屋が用意されており、学生は出席番号で表し、N={0, 1, 2, 3}としたときの部屋割りとして考えられる順列を生成し、その場合の数を計算してください。

写像で表すと次のようになります。

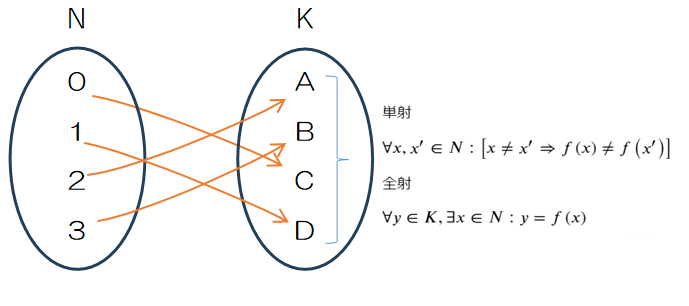
全射と単射の要件を満たす順列
全射と単射の要件を満たす順列

個室になるということは単射である順列になり、なおかつ集合Nの個数n=集合Kの個数k、であることから空き部屋が出ることがないので全射の重複順列になり、併せて全単射になります。

そこで、順列を生成するperm_injective_func関数を使いperm_injective_listを、全射の重複順列を生成するperm_surjective_func関数を使いperm_surjective_listを生成し比較します。

N=Kの場合の全単射の考え方

  1. k_list = ['A', 'B', 'C', 'D']
  2. n = 4
  3. perm_injective_list = perm_injective_func(k_list, n)
  4. perm_surjective_list = perm_surjective_func(k_list, n)
  5. if perm_surjective_list == perm_injective_list:
  6. print('surjective == injective')
  7. print('surjective = ',len(perm_surjective_list))
surjective == injective
surjective =  24

perm_surjective_list == perm_injective_listの場合はその旨を表示します。

結果は包除原理を使った全射による個数も順列の計算を使った単射による個数も一致することがわかりました。つまり、次の計算が成り立ちます。

全単射の個数

$\sum\limits_{i=0}^{n}(-1)^n\,\ _{n} C_i(n-i)^n=\ _{n} C_0n^n-\ _{n} C_1(n-1)^n+\ _{n} C_2(n-2)^n-\cdots\pm\ _{n} C_n(n-n)^n=n! $

問題の例では

全射の個数$ =\ _{4} C_0 4^4-\ _{4} C_1 3^4+\ _{4} C_2 2^4-\ _{4} C_3 1^4+\ _{4} C_4 0^4=24$

単射の個数=$n!=4!=24$

当然と言えば当然ですが、包除原理の結果と階乗の計算結果が等しくなるは不思議なことです。このあたりを突き詰めていくと面白い世界が見えてきます。

攪乱順列（モンモール問題）

攪乱順列（モンモール問題）とは

全単射の順列で特殊なものとして、モンモール問題という興味深いものがあります。フランスの数学者 ピエール・モンモールにちなむもので、非常に興味深い洞察を得ることができます。ここでは、そのさわりのみをご紹介し、さらに新たなことを習得したうえで、

問題5

5人でプレゼントの交換会をします。N={A, B, C, D, E}の5人が１つずつ別々のプレゼントを持ち寄り、でたらめに交換します。この際、自分が持参したプレゼントを受け取ることが1人もないような場合の数を計算してください。

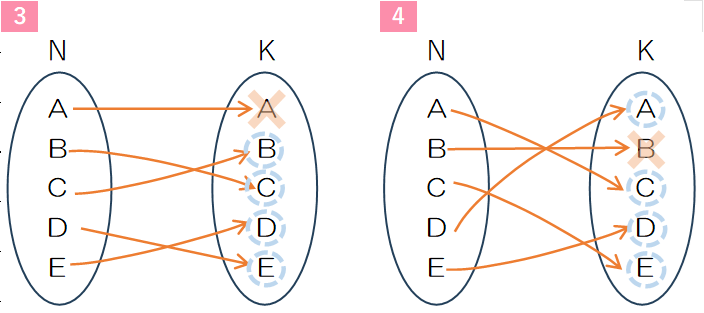
ここで生成される順列を完全順列（complete permutations）、攪乱順列（derangement）といろいろな呼び方がありますが、今後は、攪乱順列という名前で通します。また、攪乱順列の個数をモンモール数（Montmort number）といいます。攪乱順列を写像にすると集合Nから同じ要素の集合Kへの対応となりこのような写像を自己写像（self-map）といいます。これを表したのが図表1です。

攪乱順列と攪乱順列ではない例
攪乱順列と攪乱順列ではない例

要素A,B・・の後にある数字はプログラムを作成するときに使用する要素の順番を付けたものです。

図で１は攪乱順列の例で、全ての人がほかの人からプレゼントをもらっています。一方２は、AとBが自分は持ち寄ったプレゼントを受け取ることを示しており、順列ではあるけど錯乱順列ではない例になります。

モンモール問題についてはSymPyライブラリのsubfactorial関数を使い、モンモール数を計算することができます。subfactorialはまさにモンモール数を表す階乗の1つで!nのように会場の逆の表記の方法もあります。

subfactorial関数は集合の要素数を引数とします。一方、generate_derangements関数を使い、完全順列を生成することができます。この場合、集合の要素をリストなどの形式を引数とします。

攪乱順列を生成する関数

SymPyモジュールの関数

Sympyモジュールのsubfactorial関数による攪乱順列の生成

  1. from sympy import subfactorial
  2. from sympy.utilities.iterables import generate_derangements
  3. k_list=['A','B','C','D','E']
  4. n=len(k_list)
  5. sympy_derangements_list = list(generate_derangements(k_list))
  6. print('sympy_derangements(5) =',subfactorial(n))
  7. pprint.pprint(sympy_derangements_list)
sympy_derangements(5) = 44
[['B', 'A', 'D', 'E', 'C'],
 ['B', 'A', 'E', 'C', 'D'],
 ['B', 'C', 'A', 'E', 'D'],
・・
['C', 'A', 'B', 'E', 'D'],
・・
['E', 'D', 'A', 'C', 'B'],
 ['E', 'D', 'B', 'A', 'C'],
 ['E', 'D', 'B', 'C', 'A']]

1.　subfactorial関数はSymPyライブラリからインポートします。

2.　generate_derangements関数はSymPyライブラリのsympy.utilities.iterablesモジュールからインポートします。

要素数5のモンモール数は44であることがわかります。

攪乱順列を生成する関数を作成

次に、攪乱順列を生成する関数を作成します。順列を生成するperm_injective_funcをもとに、次の変更を加えます。

引数は集合Nのリストを渡すのみとします。順列の候補として配列に追加する際に、順列にするために同じ要素のものとともに配列のインデックスと要素の順番が同じ場合は配列に加えないようにします。

攪乱順列を生成する関数

  1. def perm_derangements_func(k_list):
  2. array = [[]]
  3. for cnt in range(len(k_list)):
  4. temp = array
  5. array = []
  6. for elm in temp:
  7. for num,item in enumerate(k_list):
  8. if item not in elm and cnt != num:
  9. array.append(elm + [item])
  10. return array
  12. perm_derangements_list = perm_derangements_func(k_list)
  13. if perm_derangements_list == sympy_derangements_list:
  14. print('perm_derangements_lis == sympy_derangements_list') 
perm_derangements_lis == sympy_derangements_list

8.　リストでの順番とk_listの順番が等しい場合は攪乱順列にならないのでarrayには追加しません。

モンモール数の計算と包除原理

モンモール数は包除原理を使って計算することができます。

はじめに、n=5のときの集合Nから集合Kへの順列は$5!=120$になります。これに対して、Aの1人だけ自分が持ち寄ったプレゼントを受け取ってしまうケースは３のようになるので、4!通りになります。同様に４はBが同じ目に遭うケースです。このように、$5!-5\times 4!$で計算することができます。ところが、前図の２のように上記の計算ではA,Bが自分が持ち寄ったプレゼントを受け取ることになるので、その数3!を足し戻す必要があります。

完全順列
完全順列

この計算は最終的には、全ての人が自分の持ち寄ったプレゼント受け取るという稀有なケースまで続きます。

この結果、モンモール数は次の式により計算することができます。

$\sum\limits_{i=0}^{n}(-1)^i\,\ _{n} C_i(n-i)!=\ _{n} C_0n!-\ _{n} C_1(n-1)!+\ _{n} C_2(n-2)!-\cdots\pm\ _{n} C_n(n-n)!$

$=\ _{5} C_0 5!-\ _{5} C_1 4!+\ _{5} C_2 3!-\ _{5} C_3 2!+\ _{5} C_4 1!-_{5} C_5 0!$

$=120-12-+60-20+5-1=44$

それでは、モンモール数を生成する関数を作成します。ここで使用するSciPyのcomb関数をインポートしfactorial関数を実行しておく必要があります。

包除原理でモンモール数を計算する関数

  1. def montmort_number_count(n):
  2. sigma = 0
  3. for i in range(n+1):
  4. sigma += ((-1)**i) * comb(n,i) * factorial(n-i)
  5. return int(sigma)
  7. montmort_number_count(5)
44

4.　n=kなのでそのまま計算します。

まとめ

これまで、区別のある学生を区別のある部屋に割り振ることを題材に写像の考え方を見てきました。重複順列、順列を写像という視点でまとめてみました。この際に、特に制限の場合、全射、単射の3つのパターンがあることを見てきました。個数は次の式により計算することができます。

制約なし 単射 全射
重複順列 順列 包除理論による全射
$_k\prod{_n}=k^n$ $\ _k P_n =\frac{k!}{(k-n)!}$ $\sum\limits_{i=0}^{k}(-1)^i\,\ _{k} C_i(k-i)^n$

ictsr4 All Rights Reserved.