単射としての組合せ

重複順列、順列は区別がある学生を区別がある部屋に割り振る例を考えました。これに対して組合せは、区別のないボールを色の区別のある箱に入れるという例を使い考えます。写像で考えるとラベルがない集合 $N$ にラベルがある集合 $K$ を対応させることになります。

Nにラベルを付けない単射としての組合せ

順列と組合せ

ラベル有無といってもイメージがわかないので、次の問題を考えます。

Example 2.1

(1) 0から2まで番号が付いた3つのボールを、青、黄、赤、紫、緑の5つの箱に入れるときの順列の数を計算してください。なお、各箱にはボールは1つしか入らないものとします。

(2) 前問でボールに番号がなくラベルがないとしたときの、組合せの数を計算してください。

Figure 2.1 で(1)と(2)の違いを写像により表しています。(1)は順列で、 ${}_5 P_3 =60$ 通りになります。(2)はボールのラベルがないことから、(1)では (青、赤、緑)、(青、緑、赤)、(赤、青、緑)、(赤、緑、青)、(緑、赤、青)、(緑、青、赤)の 6 個の順列を別々に数えるのに対し、(2) の組合せでは 1 通りと計算します。

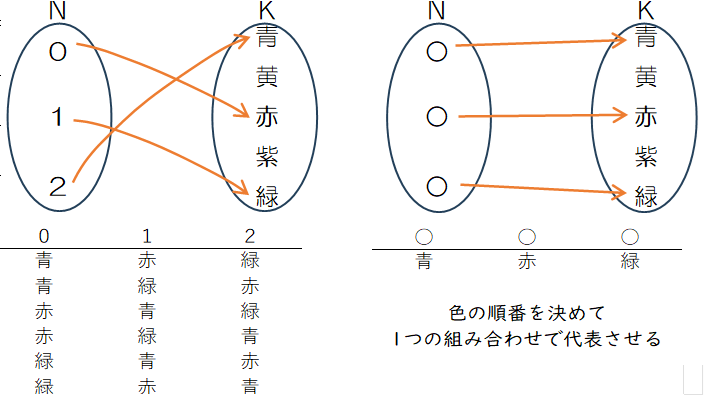
Figure 2.1　写像を使って順列と組合せを比べる
写像を使って順列と組合せを比べる

(2) の組合せの個数は、60 個の順列を選ばれた ３ つの箱の順列 $3!=6$ で割った 10 通りになります。この組合せは ${}_kC_n$ で計算することができます。

組合せを生成する関数を作成する

Nに区別がある順列の生成

組み合わせと順列の関係を見るために、前に作成したgenerete_arbitrary_permを使い、リストarbitrary_perm_listに順列を生成し、ここから組み合わせcomb_injective_listの配列に集約します。

あえて、出力しませんが次に順列の中から、組合せとして絞り込みます。

増加関数としての組合せを生成

増加関数の考え方

青、赤、緑の 3色のボールから色を選び、色の組合せを生成するには、まず各色に番号を振り（例：0=青, 1=黄, 2=赤, 3=紫, 4=緑…）、取り出すボールの順序を $x_0,x_1,x_2,\dots,x_n$ とします。ボール自体には区別がないように見えますが、ここでの「区別」とは出席番号のような恒久的なラベルではなく、取り出した順番を示す便宜的なものと考えます。

順番に取り出す際、もし最初に選んだ $x_0$ が色番号 0（青）であるとすると、次の $x_1$ は番号 0 以下（青）ではなく番号 1 以上（黄以降）から、同様に $x_2$ は選んだ $x_1$ の番号よりも大きい番号から選びます。このルールにより、取り出す順番が進むにつれて色番号は非減少（厳密には昇順）になります。

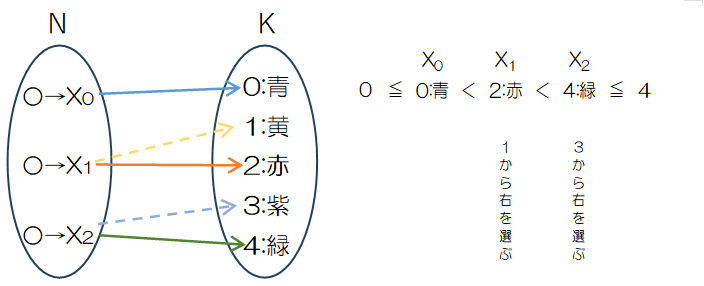
Figure 2.2　増加写像の考え方を使い組合せを生成
増加写像の考え方を使い組合せを生成

例えば、0:青, 2:赤, 4:緑を選んだ場合、2:赤, 4:緑, 0:青のような別の順列は生成されず、色の組合せ{青, 赤, 緑}が 1通りとして得られます。

このように、取り出す要素の番号が昇順となる写像を増加写像（increasing_map）と呼び、順列の中から代表的な組合せを一意に選び出す方法として用います。この考え方は、組合せのプログラムを作成するうえで非常に役立ちます。

この関係を数式にすると Python では添え字は 0 から始まり zero-based といいい図表のようになります。一方、一般的には添え字は 1 から始まり one-based といい、次のように表します。

$1 \leqq x_1\lt x_2\lt x_3 \leqq 5$

組合せの式 ${}_k C_n$ との対応を考える場合は 1 から始まる方法の方が適しているので、2 つを併記します。

そこで関係を一般化すると、つぎのようになります。

Equation 2.1　増加写像を使った組合せの表現　${}_kC_n$

zero-basedプログラミングでの方法

$0\leqq x_0\lt x_1\lt\cdots\lt x_{n-1}\leqq k-1$

one-based 一般的な考え方

$1 \leqq x_1\lt x_2\lt \cdots \lt x_n \leqq k$

増加関数の考え方を使い順列から組合せに変換する

増加写像の考え方を使い組合せを生成する関数を作成しますの generete_arbitrary_perm関数で作成した順列 arbitrary_perm_list から、増加写像の要件を満たす配列のみを抽出する関数を作成し、組合せを生成します。関数名は増加写像の意味を込めて filter_increasing_map とし、引数は順列の配列とします。

順列の配列を elm として順次読み込み、elm の中の要素よりもその 1 つ右側の要素の方が大きいことが分かった時点で、その elm は増加写像の要件を満たさなくなるので break し、次の要素を読み込みます。最後まで break されなかった elm は、組合せとしてリスト comb_list に追加します。なお、増加関数の絞り込みをするときに、単純に要素同士を比べると文字コード順となり k_list の並び順と一致しなくなるので、k_list のインデックスの順番で比較するようにします。

Code 2.1　順列を生成し、個数を表示する

  1. n = 3
  2. k_list = ['青', '赤', '緑', '黄', '紫']
  3. perm_injective_list = generate_injective_perm(k_list, n)
  4. print(
  5. f'generate_injective_perm({len(k_list)}, {n})) ='
  6. f'{len(perm_injective_list)}'
  7. )
generate_injective_perm(5, 3)) =60

3.　 generate_injective_permはあらかじめ実行しておいてください。

生成した順列を組合せ変換する関数を作成します。

Code 2.2　順列のリストから組合せに絞り込む関数

  1. def filter_increasing_map(sequence, k_list = None, strict=True, reverse=False):
  2. filtered_list = []
  3. for elm in sequence:
  4. for i in range(len(elm) - 1):
  5. if strict == True and elm[i] == elm[i + 1] :
  6. break
  7. if k_list is None:
  8. elm_cur = elm[i]
  9. elm_next = elm[i + 1]
  10. if elm_cur < elm_next if reverse else elm_cur > elm_next:
  11. break
  12. else:
  13. idx_cur = k_list.index(elm[i])
  14. idx_next = k_list.index(elm[i + 1])
  15. if idx_cur < idx_next if reverse else idx_cur > idx_next:
  16. break
  17. else:
  18. filtered_list.append(elm)
  19. return filtered_list
  21. origin = [('A', 'B', 'C'),
  22. ('A', 'C', 'B'),
  23. ('B', 'C', 'C'),
  24. ('C', 'B', 'B'),
  25. ('B', 'C', 'A'),
  26. ('C', 'B', 'A'),
  27. ]
  29. filter_increasing_map(origin)
[('A', 'B', 'C')]

5.　k_list に対して index メソッドを適用すると引数の値が k_list の何番目にあるかを返します。この index メソッドを使い、elm の i 番目の値の k_list 中での順番が、k_listi+1 番目のそれより小さい場合には、増加写像にならないので break します。このため 3.では i は 0 から elm の長さ-1 までループさせます。

7.　for ループ に対して break されないで抜けると、else 節以下の処理をします。このことにより、増加写像として残った場合のみ順列の要素が組合せとして surjective_list に追加されます。

Code 2.3　重複順列から組合せに絞り込む関数

  1. k_list = ['B', 'C', 'A']
  2. print('k_list なし')
  3. print('strict = True, reverse = False : ',
  4. filter_increasing_map(origin, strict = True, reverse = False))
  5. print('strict = True, reverse = True : ',
  6. filter_increasing_map(origin, strict = True, reverse = True))
  7. print('strict = False, reverse = False : ',
  8. filter_increasing_map(origin, strict = False, reverse = False))
  9. print('strict = False, reverse = True : ',
  10. filter_increasing_map(origin, strict = False, reverse = True))
  11. print('k_list B→C→A')
  12. print('strict = True, reverse = False : ',
  13. filter_increasing_map(origin, k_list,strict = True, reverse = False))
  14. print('strict = True, reverse = True : ',
  15. filter_increasing_map(origin, k_list,strict = True, reverse = True))
  16. print('strict = False, reverse = False : ',
  17. filter_increasing_map(origin, k_list, strict = False, reverse = False))
  18. print('strict = False, reverse = True : ',
  19. filter_increasing_map(origin, k_list,strict = False, reverse = True))
k_list なし
strict = True,  reverse = False :  [('A', 'B', 'C')]
strict = True,  reverse = True  :  [('C', 'B', 'A')]
strict = False, reverse = False :  [('A', 'B', 'C'), ('B', 'C', 'C')]
strict = False, reverse = True  :  [('C', 'B', 'B'), ('C', 'B', 'A')]
k_list B→C→A
strict = True,  reverse = False :  [('B', 'C', 'A')]
strict = True,  reverse = True  :  [('A', 'C', 'B')]
strict = False, reverse = False :  [('B', 'C', 'C'), ('B', 'C', 'A')]
strict = False, reverse = True  :  [('A', 'C', 'B'), ('C', 'B', 'B')]

3.　k_listを引数に指定しないので、コンピュータの内部的なコードを基準に絞り込みます。

11. k_listを引数に指定しているので、k_listを基準に絞り込みます。

順番もk_listと同じ並び順になりました。

Equation 2.1　組合せの個数の計算　k個からn個を選ぶ場合

$\displaystyle{}_k C_n =\frac{{}_k P_n}{n!}=\frac{k!}{n!(k-n)!} = \frac{\overbrace {k(k-1)(k-2)\cdots (k-n+1)}^{n個}}{\underbrace {n\times (n-1)\times \cdots 2 \times 1}_{n個}}$

ただし${}_kC_0=1 \quad k\lt n \rightarrow 0$

組合せは順列と同じように箱には球が1つしか入らないので単射となりますが、集合$N$ の区別がない写像になります。

組合せに関する標準ライブラリなどの関数

組合せの個数を計算するPythonの関数

Code 2.4　順列から増加関数により組合せに変換

  1. comb_from_perm_list = filter_increasing_map(perm_injective_list)
  2. print('combinations from permutation(5, 3) = ', len(comb_from_perm_list))
  3. comb_from_perm_list
combinations from permutation(5, 3) =  10
[('赤', '青', '黄'),
 ('緑', '青', '黄'),
 ('緑', '赤', '青'),
 ('緑', '赤', '黄'),
 ('紫', '青', '黄'),
 ('紫', '赤', '青'),
 ('紫', '赤', '黄'),
 ('紫', '緑', '青'),
 ('紫', '緑', '赤'),
 ('紫', '緑', '黄')]

2.　 filter_increasing_map関数を使い増加写像を抜き出します。

組合せを生成する関数

itertools モジュールの combinations関数により、組合せを生成することができます。itertools は Function Programming Module に分類されます。

引数として集合 $K$ のリスト k_list と集合 $N$ の個数 n を渡します。

Code 2.5　itertoolsモジュールを使い組合せを生成

  1. import itertools
  2. itertools_comb_list = list(itertools.combinations(k_list, n))
  3. print(
  4. f'itertools.combinations({n}, {len(k_list)}) = '
  5. f'{len(itertools_comb_list)}'
  6. )
  7. if comb_from_perm_list == itertools_comb_list:
  8. print(f'comb_from_perm_list == itertools_comb_list') 
itertools.combinations(3, 5) = 10
comb_from_perm_list == itertools_comb_list

1.　itertools モジュールは Python の標準ライブラリですが、ビルドイン関数ではないので、使用する都度、インポートする必要があります。

3.　重複順列は itertools モジュールの combinations関数を使い出力することができます。なお、combinations関数はイテレータという特殊な形式となるので、戻り値をリストとして扱うときには list関数を使い変換する必要があります。

4.　出力すると、リストの中に重複順列の各パターンがタプルにまとめられます。件数は 10 件になります。

組合せを生成する関数

前節では順列のリストから絞り込む方法で組合せを生成しましたが、n が大きくなるにしたがい順列の個数も爆発的に増えてしまい処理に時間がかかる恐れがあります。このため、重複順列を生成する generete_arbitrary_perm関数に増加写像の処理を組み込むことで組合せを生成する関数を作成します。

組合せの単射なので関数名は generate_injective_comb関数とし、これまでと同じように、引数は箱の色のリスト k_list とボールの個数 n とします。重複順列では 1 つ目に 2:赤を選んでも 2 つ目は 0:青から順次選ぶ必要がありました。一方、組合せは要素の選択順序を考慮しないため昇順に並べるのが一般的なので、2 つ目は 3:紫のから選べばよいことになります。そこで、この 3:紫に当たる番号を変数 start でコントロールします。

Code 2.6　組合せを生成する関数

  1. def generate_injective_comb(k_list, n):
  2. comb_list = [()]
  3. for _ in range(n):
  4. next_comb = []
  5. for elm in comb_list:
  6. if elm == ():
  7. start = 0
  8. else:
  9. start = k_list.index(elm[-1]) + 1
  10. for item in range(start, len(k_list)):
  11. next_comb.append(elm+(k_list[item],))
  12. comb_list = next_comb
  13. return comb_list
  15. comb_injective_list = generate_injective_comb(k_list, n )
  16. print('generate_injective_comb(5, 3) = ',len(comb_injective_list))
  17. if (
  18. comb_from_perm_list
  19. == itertools_comb_list
  20. == comb_injective_list
  21. ):
  22. print(
  23. 'from arbitrary == surjective == monotonic'
  24. )
generate_injective_comb(5, 3) =  10
from arbitrary == surjective == monotonic

3.　選ぶ色の数 n が埋まるまでループさせます。

8.　変数 start 組合せの次の要素を選ぶときに、k_list のどの indeｘから選べばよいかを示します。初めのボールは 0:青からが候補になるので start を 0 に設定します。2 つ目以降のボールを入れる箱を選ぶときは、前に選んだ色番号の次からが候補になりあます。

10. k_list.index(elm[-1])は最後に選んだ k_index での順番が代入されているので、この番号+1 を start に代入します。

11. start から k_list 最後の要素まで色番号を順次選び、タプルとして追加した新しい要素を comb_injective_list に追加します。

12. 全ての繰り返しが終わった後、最終的に生成された組合せを戻り値として返します。

18. 作成した組合せを、リスト comb_injective_list に代入します。

20. Python では 3 つのリストをつなげて、それぞれが等しいかを判断することができます。itertools、順列から選んだ組合せ、及びここで作成した組合せを比較し、全てが等しければ、その旨を表示します。

インデックスの考え方が少し面倒ですが、重複順列のプログラムを少し修正するだけで組合せを生成する関数を作成することができました。

いったん順列を作成してから絞り込むと、情報量が膨れ上がってしまいますが、generate_injective_comb関数では、作成段階で絞り込めるので効率的であると考えられます。

ictsr4 All Rights Reserved.