全射、単射の制限がない重複組合せ

写像から見た重複組合せ

組合せは集合 $K$ から 1 つしか選ぶことができませんが、重複組合せでは重複して選ぶことができます。このため、組合せに比べ複雑になりますが、写像と増加関数の考え方を使うと簡単に整理することができます。

重複組合せの考え方

単射の組合せとの違いを見るため、次の問題を考えます。

Example 2.2

区別の無い 5 つのボールを、青、赤、緑の色がついた 3 つの箱に入れるとするときの場合の数を計算してください。なお、各箱には重複してボールを入れることができ、空の箱があってもよいものとします。

写像にすると、左の図のようになり、集合 $K$ の要素は空白も複数の要素から対応付けられるので、組合せは単射で定義域である集合 $N$ について区別されない写像になります。また、増加関数の考え方を使うため、集合 K の色には色番号を付けます。一方、重複組合せは全射や単射の制限がない写像になります。

Code 2.7　重複順列からフィルター

k_list = ['青', '赤', '緑']
n = 5
arbitrary_perm_list = generete_arbitrary_perm(k_list, n)
print(
'generete_arbitrary_perm(5, 3) =',
len(arbitrary_perm_list)
)

generete_arbitrary_perm(5, 3) = 243

3.　重複順列から絞り込みます。

重複組合せを生成する関数

itertool モジュールの combinations_with_replacement関数により、重複組合せを生成することができます。引数は集合 $K$ のリストと、集合 $N$ の個数を渡し、重複組合せの一覧がジェネレータとして返します。

Code 2.8　itertoolsモジュールを使い重複組合せを生成する

itertools_arbitrary_list = list(itertools.combinations_with_replacement(k_list, n))
print('itertools.combinations_with_replacement(3, 5)= ', len(itertools_arbitrary_list))
itertools_arbitrary_list

itertools.combinations_with_replacement(3, 5)=  21
[('青', '青', '青', '青', '青'),
 ('青', '青', '青', '青', '赤'),
 ('青', '青', '青', '青', '緑'),
 ('青', '青', '青', '赤', '赤'),
 ('青', '青', '青', '赤', '緑'),
 ('青', '青', '青', '緑', '緑'),
 ('青', '青', '赤', '赤', '赤'),
 ('青', '青', '赤', '赤', '緑'),
 ('青', '青', '赤', '緑', '緑'),
 ('青', '青', '緑', '緑', '緑'),
 ('青', '赤', '赤', '赤', '赤'),
 ('青', '赤', '赤', '赤', '緑'),
 ('青', '赤', '赤', '緑', '緑'),
 ('青', '赤', '緑', '緑', '緑'),
 ('青', '緑', '緑', '緑', '緑'),
 ('赤', '赤', '赤', '赤', '赤'),
 ('赤', '赤', '赤', '赤', '緑'),
 ('赤', '赤', '赤', '緑', '緑'),
 ('赤', '赤', '緑', '緑', '緑'),
 ('赤', '緑', '緑', '緑', '緑'),
 ('緑', '緑', '緑', '緑', '緑')]

1　重複組合せはitertoolsモジュールのcombinations_with_replacement関数で生成することができます。

一部省略していますが、全部で 21通りの組合せが考えられます。

「しきり」による考え方

「しきり」による重複組合せの計算

重複組合せを写像と、一般的に使われる分割の「しきり」とボールであらわす方法で考えます。この方法を使い、重複組合せのいくつかのパターンで整理します。

①典型的な重複組合せ

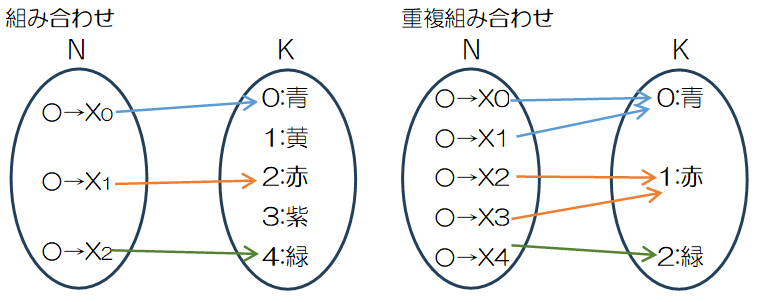
5 個の区別の無いボールを並べ、その間に青と赤を分ける「しきり」と赤と緑を分ける「しきり」を入れます。このケースは青2 個、赤2 個、緑 1 個とまっとうな組合せになります。

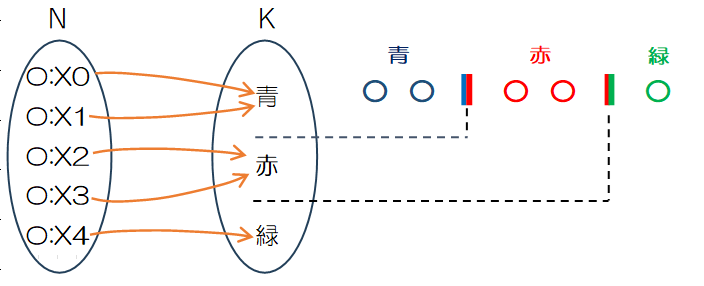
②端ではない色が選ばれない場合

制約なしの場合、青3 つ緑 2 つが選ばれ、真ん中の赤が選ばれないようなケースも認められます。この場合、青と赤を分ける「しきり」と、赤と緑を分ける「しきり」が青と緑の間に並びます。

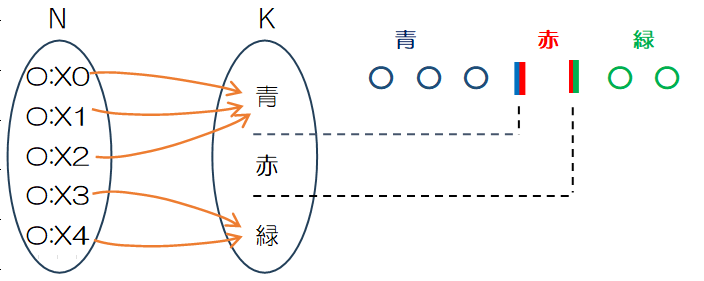
③端の色が選ばれない場合

右端の色は緑になりますが、この場合、Figure 2.6のように一番右側に赤と青の「しきり」が入ります。

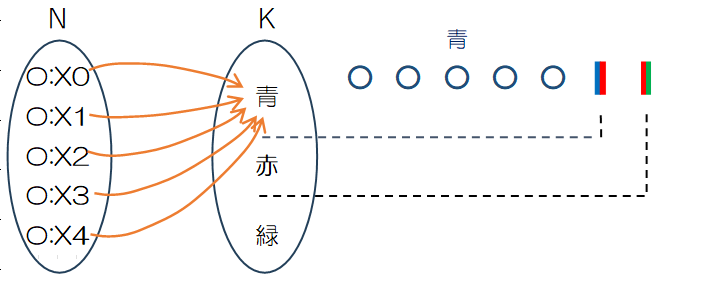
3つのケースを見ると、「しきり」2つとボール5つを7つのマスに並べる際の組合せを計算することで重複組合せの個数を計算することができます。

一般化すると、ボールの数nと「しきり」の数(k-1)を足したn+k-1個の中からボールn個を選ぶことになります。また「しきり」の方に注目すれば、仕切りk-1個を選ぶことと同じ意味になります。このような区別なないn個のボールをk色の箱に重複を許して選ぶ重複組合せの個数を${}_k H_n$で表し、計算式は次の通りです。

Equation 2.3　n個からk個選ぶ重複組合せの個数　${}_k H_n$

${}_k H_n = {}_{n+k-1}C_n={}_{n+k-1}C_{k-1}$

増加写像としての重複組合せ

増加写像の考え方

重複組合せを増加組合せの数式で表すと、組合せとは異なり前と同じ色を選んでもよいので、図の①のように$0\leqq x_0\leqq x_1 \leqq x_2\leqq x_3\leqq x_4\leqq 2$となります。ところで$x_i$は整数なので$x_i\leqq x_{i+1}\leftrightarrows x_i\lt x_{i+1}+1$となり、$\ 0\leqq x_0\lt x_1+1\lt x_2+2\lt x_3+3\lt x_4+4 \leqq2+4=6$と書き換えることができます。ここで、$y_i=x_i+1 (i=0,1,2,\cdots ,k-1)$を代入すると$\ 0\leqq y_0\lt y_1\lt y_2\lt y_3\lt y_4\leqq 6$となり図の下のようになります。

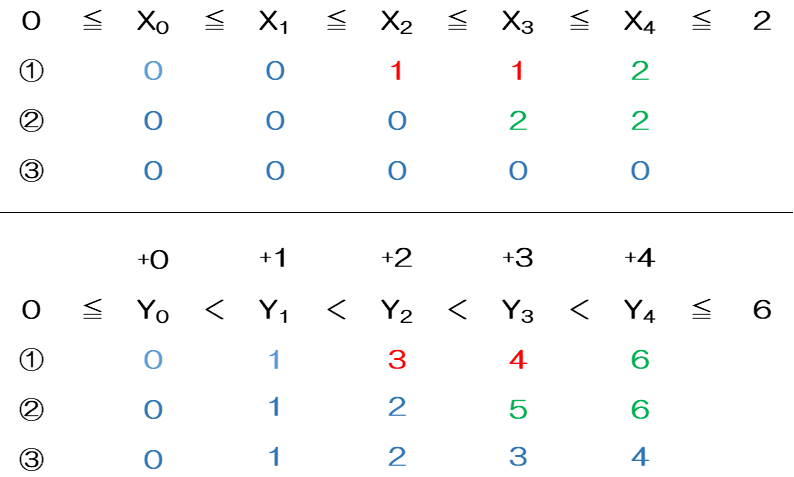
①の $x_4$ の最大値は 2 なので、$y_4$ の最大値は 6 となるところに注意が必要です。次に 1 始まりの方法を考えます。

$1 \leqq x_1\leqq x_2\leqq x_3\leqq x_4\leqq x_5\leqq 3$

$\leftrightarrows 1\leqq x_1\lt x_2+1\lt x_3+2\lt x_4+3\lt x_5+4\leqq 3+4=7$となります。$y_i=x_i+i-1 (i=1,2,3\cdots ,k)$を代入すると$1\leqq y_1\lt y_2\lt y_3\lt y_4\lt y_5\leqq =7$となり、${}_7C_5$となります。

結果的に①の全ての組合せを集合1、②の全ての組合せを集合２とすると、集合１から集合２の各項に0,1,2,3,4を足した写像であり、逆に集合2は集合2から集合Ⅰへの対応は各項から0,1,2,3,4を引いた写像となり、2 つの集合は逆写像がとなるので全単射となり個数が等しくなります。

ただし、コンピュータの世界では添え字は 0 から始まりますが、一般的には 1 から始まるので、それに倣うと次のように表現します。

$1\leqq y_1\lt y_2\lt y_3\lt y_4\lt y_5\leqq 3+4=7$

この関係を一般化すると、つぎのようになります。

Equation 2.4　重複組合せを増加関数で表す式

zero-based

$0 \leqq x_0\leqq x_1\leqq \cdots \leqq x_{n-1} \leqq k-1$

$\leftrightarrows 0 \leqq x_0 \lt x_1+1 \lt x_2 +2 \cdots \lt x_{n-1}+n-1 \leqq n+k-2$

$\because x_i\leqq x_{i+1} \leftrightarrow x_i\lt x_{i+1}+1$

$y_i=x_i+1 (i=0,1,2,\cdots ,k-1)$

$\leftrightarrows 0\leqq y_0\lt y_1\lt y_2 \cdots y_{n-1}\leqq n+k-2$

one-based

$1 \leqq x_1\leqq x_2\leqq \cdots \leqq x_n \leqq k$

$\leftrightarrows 1 \leqq x_1 \lt x_2+1 \lt x_3 +2 \cdots \lt x_n+n-1 \leqq n+k-1$

$\because x_i\leqq x_{i+1} \leftrightarrow x_i\lt x_{i+1}+1$

$y_i=x_i+i-1 (i=1,2,3\cdots ,k)$

$\leftrightarrows 1\leqq y_1\lt y_2\lt y_3 \cdots y_n\leqq n+k-1$

${}_k H_n = {}_{n+k-1} C_n={}_{n+k-1} C_{k-1}$

写像の考え方によると、重複組合せのような対応を広義の増加写像といい、組合せを狭義の増加写像といいます。組合せは単射の対応であったように、狭義の増加写像であることと単射は同じことをいいます。

重複組合せを生成する関数

Code 2.9　重複組合せの個数を計算

def H(k, n):
return C(n+k-1, n)
print('H(3 ,5)=', H(3, 5))

H(3 ,5)= 21

2.　あらかじめC関数を実行しておく必要があります。

重複組合せをイメージするのには少し努力が必要ですが、その一覧を生成するプログラムは組合せの生成のプログラムを広義の単調増加関数にするため、1つだけ変更を加えるだけです。

Code 2.10　制約なしの写像としての重複組合せを生成する

def generate_arbitrary_comb(k_list, n):
comb_list = [()]
for cnt in range(n):
temp = comb_list
comb_list = []
for elm in temp:
if elm == ():
start = 0
else:
start = k_list.index(elm[-1]) # +
for item in range(start, len(k_list)):
comb_list.append(elm + (k_list[item],))
return comb_list
k_list = ['青', '赤', '緑']
n = 5
comb_arbitrary_list = generate_arbitrary_comb(k_list, n )
print('injective=', len(comb_arbitrary_list), 'H関数', H(len(k_list), n))
comb_arbitrary_list == comb_arbitrary_list injective= 21 H関数 21.0

[('青', '青', '青', '青', '青'),
 ('青', '青', '青', '青', '赤'),
 ('青', '青', '青', '青', '緑'),
 ('青', '青', '青', '赤', '赤'),
 ('青', '青', '青', '赤', '緑'),
 ('青', '青', '青', '緑', '緑'),
 ('青', '青', '赤', '赤', '赤'),
 ('青', '青', '赤', '赤', '緑'),
 ('青', '青', '赤', '緑', '緑'),
 ('青', '青', '緑', '緑', '緑'),
 ('青', '赤', '赤', '赤', '赤'),
 ('青', '赤', '赤', '赤', '緑'),
 ('青', '赤', '赤', '緑', '緑'),
 ('青', '赤', '緑', '緑', '緑'),
 ('青', '緑', '緑', '緑', '緑'),
 ('赤', '赤', '赤', '赤', '赤'),
 ('赤', '赤', '赤', '赤', '緑'),
 ('赤', '赤', '赤', '緑', '緑'),
 ('赤', '赤', '緑', '緑', '緑'),
 ('赤', '緑', '緑', '緑', '緑'),
 ('緑', '緑', '緑', '緑', '緑')]

10.　1つの箱が選択されたのち、次の箱を選ぶときには前と同じものを選ぶことも許されます。このため、startを選ぶときにstart = k_list.index(elm[-1])として組合せの時の#+1を削除するだけの変更になります。

増加写像の考え方は、プログラムを作成するうえではすごい威力を発揮することがわかります。