全射としての重複組合せ

1 全射の重複組合せの考え方

重複組合せは単射や全射の制限がない一般写像であり空箱を許しますが，この章では各箱が必ず１個以上のボールを受け取る全射の場合を扱います。一般写像と全射の重複組合せを比較するため、次の問題を考えます。

Example 2.3

区別のない 7 つのボールを、青、赤、緑の色がついた 3 つの箱に入れるときの場合の数を計算してください。なお、各箱には重複してボールを入れることができ、空の箱が出ることは許されないものとします。

重複順列の全射の計算は包除原理を使い複雑な計算をしました。重複組合せになり、集合 $N$ が区別されなくなった場合、どのような違いがあるでしょうか。

制約なしの写像の重複組合せを全射に変換

generate_arbitrary_comb関数を使い重複組合せを生成したのち、全ての色が選ばれる組合せのみを抽出することにより、全射の重複組合せを生成します。

Code 2.11　制約なし写像の重複組合せから全射の組合せを抽出

k_list = ['青', '赤', '緑']
n = 7
comb_arbitrary_list = generate_arbitrary_comb(k_list, n)
comb_list_from_arbitrary = []
for elm in comb_arbitrary_list:
if is_surjective(elm, k_list):
comb_list_from_arbitrary.append(elm)
print(
f'generate_arbitrary_comb({len(k_list)}, {n}) :'
f' count = {len(comb_arbitrary_list)}'
)
print(
f'comb_list_from_arbitrary :'
f' count = {len(comb_list_from_arbitrary)}'
)
comb_list_from_arbitrary

generate_arbitrary_comb(3, 7) : count = 36
comb_list_from_arbitrary    : count = 15
[('青', '青', '青', '青', '青', '赤', '緑'),
 ('青', '青', '青', '青', '赤', '赤', '緑'),
 ('青', '青', '青', '青', '赤', '緑', '緑'),
 ('青', '青', '青', '赤', '赤', '赤', '緑'),
 ('青', '青', '青', '赤', '赤', '緑', '緑'),
 ('青', '青', '青', '赤', '緑', '緑', '緑'),
 ('青', '青', '赤', '赤', '赤', '赤', '緑'),
 ('青', '青', '赤', '赤', '赤', '緑', '緑'),
 ('青', '青', '赤', '赤', '緑', '緑', '緑'),
 ('青', '青', '赤', '緑', '緑', '緑', '緑'),
 ('青', '赤', '赤', '赤', '赤', '赤', '緑'),
 ('青', '赤', '赤', '赤', '赤', '緑', '緑'),
 ('青', '赤', '赤', '赤', '緑', '緑', '緑'),
 ('青', '赤', '赤', '緑', '緑', '緑', '緑'),
 ('青', '赤', '緑', '緑', '緑', '緑', '緑')]

6.　重複組合せの組合せを集合に変換し、集合 $K$ の全要素 k_list を集合に変換したものと等しければ全射であると判断します。

全射の重複組合せの数を数えたり生成したりする関数は、Python の既存のライブラリには見当らないので、別の視点から計算し結果を照合することにより正しく計算できていることを確認します。

ボールと「しきり」の考え方で個数を計算する

ボールと「しきり」の考え方

前項のなかで制約なしの重複組合せを 3 つのパターンで整理しました。このうち全射となると①「典型的な重複組合せ」のみが対象となり、②「一部の色が選ばれない」のように「しきり」が隣り合ったり、③「端の色が選ばれない場合」のように「しきり」が両端に来たりするものは許されません。

そこで、ボールと「しきり」を混ぜた中からボールまたは「しきり」を選ぶのではなく、Figure 2.8のように、n=7、k=3 の場合、6 か所のうち 2 か所に「しきり」を入れる組合せを計算することにより、全射の重複組合せの個数を求めることができます。

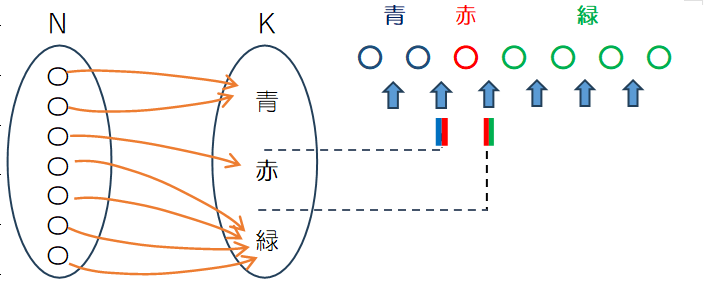
${}_6 C_2={}_6 C_4=15$通りになります。一般化すると n-1 個のすき間から k-1 個を選んでしきりを入れるので ${}_{n-1} C_{k-1}$ となります。その結果、全射の重複組合せの個数は ${}_{n-1} C_{k-1}={}_{n-1} C_{n-k}$ の式で計算することができます。

整理のため、単射の組合せ、一般写像の重複組合せ、及び全射の重複組合せについてまとめると次のようになります。

組合せ、重複組合せの個数を計算する関数

重複組合せの個数を計算する関数も既存のライブラリには見当たらないので、独自に作成します。関数名もシンプルにHとし、引数は k と n の個数とし、重複組合せを求める場合は、オプションで制約なしの場合は” u ”、全射の場合は” s ”を指定します。なお、実行する際には C関数を使用するのであらかじめ実行しておきます。

docstring 文字列としては存在するものの、どこにも代入されていないため、実行時には何も起きません

Code 2.12　重複組合せの個数を計算する関数

def H(k, n ,option='u'):
"""
n個の要素から重複を許してk個を取り出す重複組合せの個数を計算
Parameters:
-----------
k : int
kの要素数
n : int
nの要素数。
option : str, optional, default='u'
組合せの生成方法を指定するオプション。
'u' (arbitrary):選ばれない要素を許す制約なしの重複組合せ
's' (surjective): 1つは選ばれる必要がある全射の重複組合せ
Returns:
--------
int
重複組合せの個数
"""
if option == 'u':
return C(n + k - 1, k - 1)
if option == 's':
return C(n - 1, k - 1)
k = 3; n = 7
print(f"arbitrary : H({k}, {n}, 'u') = {H(k, n, 'u')}")
print(f"surjective : H({k}, {n}, 's') = {H(k, n, 's')}")

arbitrary : H(3, 7, 'u') = 36
surjective : H(3, 7, 's') = 15

1.　引数 option='u'とすることで、制約なし写像の重複組合せをデフォルトとします。

2.　複数行にわたるコメントを入れるときは’’’ ‘’’で囲います。行単位のコメントとは異なり、通常のプログラムのコードを書くときと同じように、インデントを合わせる必要があります。ここでのコメントは docstring といい、”? H ”と入力すると表示されます。

n=7、k=3 の場合、制約なしの重複組合せは 36 通りに対し、全射にすると 15 通りに絞られることになり、${}_6 C_2={}_6 C_4=15$ 通りと一致することを確認することができました。

全射の重複組合せを生成する関数

itertools など既存のライブラリにも全射の重複組合せを生成する関数は見当たりません。もちろんCode 2.11の方法でも生成は可能ですが、制約なし写像の配列から抽出するのは無駄が生じます。そこで、全射の特性を活かしながら 2 つの考え方で関数を作成します。

あらかじめ各色を1つずつ選び全射の要件を担保

全射の重複組合せを計算、生成する場合、Figure 2.9のようにはじめに k 個の色にボールを 1 つずつ選んで全射である状態を確保した上で、残りのボールを制約なしで重複組合せを計算するテクニックがあります。

全射の場合、集合 $K$ から全ての要素を少なくとも 1 つは選ぶ必要があるので、はじめに k 個の色の箱に順次ボールを入れて全射の要件を担保したのち、残った n-k 個のボールを一般写像として割り振ればよいことになります。ここではFigure 2.9に沿って具体的な手順を追っていきます。

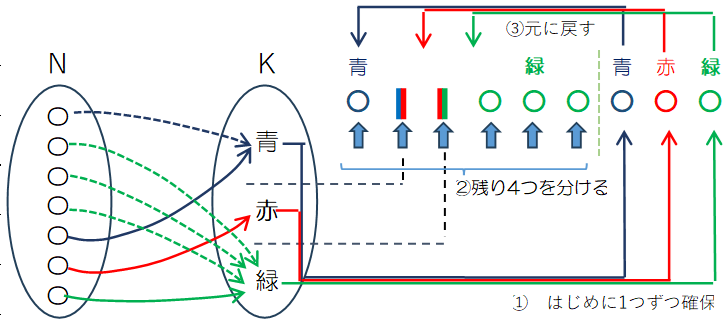
3 個のボールに対して青、赤、緑の色をそれぞれ対応させ、全射であることを確保します。

残り 4 個のボールについて、制約なし写像で重複組合せを生成します。ここでは赤が選ばれていませんが、①ですでに 1 つ確保されているので問題ありません。

②の個数は ${}_4 H_3 ={}_6 C_4=15$ となり、全射の重複組合せの個数と一致します。

①と②を結合したものが全射の重複組合せになります。

一般化すると、全射の重複組合せの個数は ${}_k H_{n-k} ={}_{n-1} C_{n-k}$ となり、Equation 2.5と一致します。

さっそく、全射の重複組合せを生成するプログラムを作成します。generate_arbitrary_comb 関数を使用し、k 個の全射を確保するため n-k 個で重複組合せを生成したのち、はじめの k_list と結合します。generate_arbitrary_comb 関数で生成する各組合せはタプルなので、リストである k_list と直接に結合することができないので注意が必要です。また、結合したリストは、きれいにならんでいないので、sort関数を使い、整列する必要があります。このとき、sort関数の適用においては k_list の順番をもとに並べ替えるようにします。

Code 2.13　k_listを確保して後から追加する方法で全射の重複組合せを生成

def generate_surjective_comb_prefix(k_list, n):
comb_list = []
for elm in generate_arbitrary_comb(k_list, n - len(k_list)):
merged = list(elm) + k_list
sorted_merged = sorted(merged, key=lambda x: k_list.index(x))
new_elm = tuple(sorted_merged)
comb_list.append(new_elm)
return comb_list
comb_surjective_prefix_list = generate_surjective_comb_prefix(
k_list,
n
)
print(
f'comb_surjective_prefix_list :'
f' count = {len(comb_surjective_prefix_list)}'
)

comb_surjective_prefix_list : count = 15

3.　 n から k_list の要素を 1 つずつ取り除き、generate_arbitrary_comb を使い生成した重複組合せを順次 elm として取り出します。

4.　 elm はタプルなのでリストに変換し、k_list と結合した結果が全射の重複組合せ merged となります。

5.　 merged は。要素ごとにきれいにならんでいないので、sorted関数を使い整列します。この際に、key=lambda x: k_list.index(x)を指定することにより k_list の順番に並べ替えます。

件数は正しいことが分かりました。内容が正しいかは最後に確認します。

増加関数の考え方を使う方法

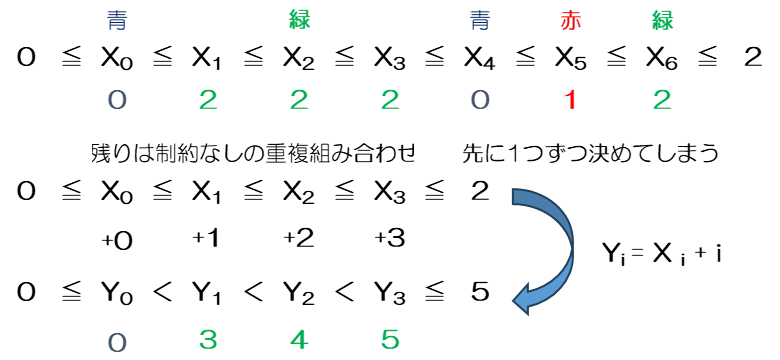
全射の重複組合せを増加関数の数式であらわすのは簡単ではありませんが、$a \lesssim b$ を「 $b$ は $a$ に等しいか、$a$ より 1 だけ大きい」 $a \leqq b \leqq a+1$ というような記号を独自に定義すれば何とか表現することができます。

自然数

$0 = x_0\lesssim x_1\lesssim \cdots \lesssim x_{n-1} = k-1$

ここでは次の３点がポイントになります。

$x_0$ は必ず 0 番目の要素になるので 0 になります。

$x_1$ 以降は前の要素と同じが 1 つ大きいという $\lesssim b$ で表します。

最後の要素は k_list の最後の要素（k-1 番目）と等しくなります。

増加関数を使ったプログラムを実現するために、次の工夫をします。

作成する組合せのはじめの要素に $k_0$ の色（青）をはじめから入れておきます。

$\lesssim$記号（等しいか 1 つ大きい）を実現するため、1 つ前の要素を読み込み、次の要素は前と同じ色からその次の色までを選ぶようにします。

最後の要素 $x_{n-1}$ は k_list の最後の色とするため、現在作成している要素の場所を n_index、現在選択した色が k_index の何番目かを把握し、残りいくつか n-n_index と残りの色が何色あるか k_k_index を比べることにより、ここからどう頑張っても全射にならない組合せのものは候補から外すようにします。

Code 2.14　増加関数の考え方を使い全射の重複組合せを生成する

def generate_surjective_comb(k_list, n):
comb_list = [(k_list[0],)]
for cnt in range(1, n):
next_comb = []
for elm in comb_list:
start = k_list.index(elm[-1])
end = min(start + 2, len(k_list))
for k_index in range(start, end):
if n - cnt >= len(k_list) - k_index :
next_comb.append(elm + (k_list[k_index],))
comb_list = next_comb
return comb_list
comb_surjective_list = generate_surjective_comb(k_list, n)
if (
comb_list_from_arbitrary
== comb_surjective_prefix_list
== comb_surjective_list
):
print(
f'comb_arbitrary_list'
f'== comb_surjective_prefix_list'
f'== comb_surjective_list'
)

comb_arbitrary_list== comb_surjective_prefix_list== comb_surjective_list

3.　 new_elm には、elm と 1 つずつ全射の重複組合せを作成します。全射であることから、1 番目の要素は青(k_list[0])として初期化します。

6.　読み込んだ要素を順次 new_elm に追加ますが、前の色と変わったときは、初めに確保しておいた色を追加します。

11. elm に２番目以降の色が含まれていないと、その色が欠けてしまうので、追加します。選ぶ色は start から start+1（プログラム上は+2）までとします。最後の（n-1）番目の要素を選ぶときは start+1 にするとリストの数を超えてエラーになるので min関数で k_list の大きさで止めるようにします。

12. 上記③の条件を満たすため場合のみ comb_list に候補として追加します。

正しく計算することができました。制約なしの候補を作ってから全射の条件で絞り込むより、作成段階で条件に合わないものを切り捨てていく方が、効率が良くなることが期待されます。

やはりこの場合も ${}_k H_{n-k} ={}_{n-1} C_{n-k}={}_{n-1} C_{k-1}$ と同じ式で表すことができます。

組合せの関数をまとめる

組合せおよび重複組合せを生成する関数をまとめる

これまで単射、一般写像および全射の組合せを生成する関数を作成してきました。基本的な流れはほぼ同じで、それぞれ少しずつ修正を加えることで機能を実現することができました。そこで、これらの 3 つの関数をまとめた generate_combinations関数を作成します。

このため、3 つ目の引数は option とし、次に通り設定します。

'i' (injective): 組合せ　default

'u' (arbitrary): 重複組合せ

's' (surjective):全射の重複組合せ

なお、このように決めごとをしても、関数を使う人にはわからないし、この関数の中では誤った option を指定した場合のエラー処理も含まれていないので、docstring を追加します。

Code 2.15　組合せを生成する関数

def generate_combinations(k_list, n, option='i'):
"""
与えられたリストk_listから、n個の要素の組合せを生成する関数。
Parameters:
-----------
k_list : list
組合せを生成するための要素のリスト。
n : int
生成する組合せの要素数。
option : str, optional, default='i'
組合せの生成方法を指定するオプション。
'i' (injective): 要素が増加する順序で組合せを生成する（昇順組合せ）。
'u' (arbitrary): 要素の順序を考慮せず、同じ要素を繰り返し使用可能な組合せを生成する（重複組合せ）。
's' (surjective): 重複を許さず、全ての要素を使用した組合せのみを生成する（全射組合せ）。
Returns:
--------
list of tuples
生成された組合せのリスト。各組合せはタプルとして表現される。
"""
comb_list = [()]
for cnt in range(n):
temp = comb_list
comb_list = []
for elm in temp:
if cnt == 0:
if option =='s':
comb_list.append((k_list[0],))
continue
else:
start = 0
else:
start = k_list.index(elm[-1]) + (1 if option == 'i' else 0)
end = len(k_list) if option != 's' else min(start + 2, len(k_list))
for k_index in range(start, end):
if option != 's' or n - cnt >= len(k_list) - k_index:
comb_list.append(elm + (k_list[k_index],))
return comb_list
k_list = ['青', '赤', '緑', '黄', '紫']
n = 3
if comb_injective_list == generate_combinations(k_list, n, option='i'):
print('injective(3,7) Ok',len(comb_injective_list))
k_list = ['青', '赤', '緑']
n = 5
if comb_arbitrary_list == generate_combinations(k_list, n, option='u'):
print('arbitrary(3,5) Ok',len(comb_arbitrary_list))
# combinations_func(k_list, n, option='u')
k_list = ['青', '赤', '緑']
n = 7
if comb_surjective_list == generate_combinations( k_list, n, option='s'):
print('surjective(3,7) Ok', len(comb_surjective_list))

injective(3,7) Ok 10
arbitrary(3,5) Ok 21
surjective(3,7) Ok 15

31. 増加写像を使って組合せを生成するので、１つの項目を選んだあと次の項目を k_list の何番目から追加するのかを start に代入します。単射である純粋増加写像の場合は前のインデックス+1、それ以外は前のインデックスにするため 0 になります。1 if option == 'i' else 0 は三項演算子といい、条件文を 1行で書くことができます。

33.　組合せを 1 つ 1 つ作成するために、elm に選んだ色を追加しますが、全射の場合のみ一番最後(cnt==n-1)のときだけ、全射にならない組合せを(len(set(new_elm)) != len(k_list)))で判断して comb_list に追加しないようにします。

generate_combinations関数を使い、これまで例として扱ってきたケースについて組合せを計算すると、結果が正しいことがわかります。