不定方程式、不定不等式

不定方程式

重複組み合わせにはさまざまな応用範囲があります。ここでは、その1つである不定方程式のいろいろなケースについてみていきます。

制約なしの場合

不定方程式を写像であらわす

重複組み合わせの考え方を使うと、次のような整数の問題も簡単に解決することができます。

Example 2.1

次の条件を満たす$x_1,x_2,x_3$の組み合わせの数を計算してください。

$x_1+x_2+x_3=10\quad(x_i\geqq0)$

変数が3つあり、式が1つだから答えは1つに決まりません。このように複数の解があるような式を不定方程式(indefinite equation)といいます。重複組み合わせと不定方程式は一見すると関係がないように思えますが、写像にしてみると同じ形をしています。

ここでは、$x_i$の組の一覧を作成し個数を解の数を計算します。$x_i\geqq0$という条件なので、全射でも単射でもない制約なし(unristricted)のタイプになります。この関係も写像であらわします。

Figure 2.1　写像で不定方程式を考える
写像で不定方程式を考える

写像を見ると、この問題は区別のない10個ボールを3つの箱に空箱も許して分ける重複組み合わせと同じ枠組みであることがわかります。また、$x_i\geqq0$なので$ x_2=0$となる右側のものも許されます。

不定方程式のもととなる重複組み合わせを作成する

そこで、まず$K={X_1, X_2, X_3}$、n=10として重複組み合わせを生成し、その個数を計算します。

Code 2.1　不定方程式を重複組み合わせで解く

  1. k_list = ['x1', 'x2', 'x3']
  2. n = 10
  3. k=len(k_list)
  4. comb_unrestrict_list = generate_unrestrict_comb(k_list, n )
  5. print('generate_unrestrict_comb 関数で生成: ', len(comb_unrestrict_list))
  6. print('重複組み合わせ H(3,10)：', H(k,n),': 組み合わせ C(12,10)：',comb(n + k - 1, n, exact = True))
  7. comb_unrestrict_list
generate_unrestrict_comb 関数で生成:  66
重複組み合わせ H(3,10)： 66 : 組み合わせ C(12,10)： 66
[('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x2'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x3'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x2', 'x2'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x2', 'x3'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x3', 'x3'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x2', 'x2', 'x2'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x2', 'x2', 'x3'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x2', 'x3', 'x3'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x3', 'x3', 'x3'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x2', 'x2', 'x2', 'x2'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x2', 'x2', 'x2', 'x3'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x2', 'x2', 'x3', 'x3'),
 ('x1', 'x1', 'x1', 'x1', 'x1', 'x1', 'x2', 'x3', 'x3', 'x3'),
・
・
('x3', 'x3', 'x3', 'x3', 'x3', 'x3', 'x3', 'x3', 'x3', 'x3')]

3.　 generate_unrestrict_comb関数を使い、その返り値を配列comb_unristrict_listに代入します。

5.　comb_unristrict_listの個数を計算します。

7.　k=3,n=10の重複組み合わせの数をH関数で計算するとともに、comb関数で${}_{n+k-1} C_{k-1}$を計算します。両者が一致することが確認できます。

X1からX3までの組み合わせを生成することができました。件数を求めることができたので、次にその一覧を生成します。

重複組み合わせで不定方程式を解く

一覧表は、solution_listに作成します。#11で作成したcomb_unristrict_listの組み合わせを、1つずつelmに読み込んで集計します。

Code 2.2　重複組み合わせから不定方程式を解く

  1. solution_list = []
  2. for elm in comb_unrestrict_list:
  3. cnt = [0] * len(k_list)
  4. for item in elm:
  5. cnt[k_list.index(item)] += 1
  6. solution_list.append(cnt)
  7. solution_list
[[10, 0, 0],
 [9, 1, 0],
 [9, 0, 1],
 [8, 2, 0],
 [8, 1, 1],
 [8, 0, 2],
 [7, 3, 0],
 [7, 2, 1],
 [7, 1, 2],
 ・
・
 
[0, 3, 7],
 [0, 2, 8],
 [0, 1, 9],
 [0, 0, 10]]

2.　#13で作成した重複組み合わせを1件ずつ読み込みます。

3.　$x_0$から$x_{k-1}$までのk_listの要素ごとの個数を計算するための配列cntを定義します。

5.　配列cntを使い$x_0,x_1,x_2$数の数をカウントします。

6.　1つの組み合わせについてカウントが終了したら配列を1つの解としてsolution_listに追加します。

不定方程式を解く関数を作成する

これまでのように一つ一つの重複組み合わせを集計するのではなく、直接解を求める関数を作成します。関数名は制約なしの不定方程式という意味でsolve_unrestricted_equationとします。引数として変数の個数をk、式の合計をnとして方程式の解を生成します。

Code 2.3　重複組み合わせから制約なしの不定方程式を解く

  1. def solve_unrestricted_equation(k, n):
  2. solution_list = [()]
  3. for kth in range(k):
  4. temp = solution_list
  5. solution_list = []
  6. for elm in temp:
  7. if kth < k-1:
  8. for nth in range(n + 1):
  9. if sum(new_elm := elm + (nth,)) <= n:
  10. solution_list.append(new_elm)
  11. else:
  12. break
  13. else:
  14. solution_list.append(elm + (n-sum(elm),))
  15. return solution_list
  16. n = 10
  17. k = 3
  19. equation_unrestricted_list = solve_unrestricted_equation(k, n)
  20. print('solve_unrestricted_equation 関数で生成:', len(equation_unrestricted_list))
  21. print('重複組み合わせ H(3,10)：', H(k,n),': 組み合わせ C(12,10)：',comb(n + k - 1, n, exact = True))
  22. equation_unrestricted_list
solve_unrestricted_equation 関数で生成: 66
重複組み合わせ H(3,10)： 66 : 組み合わせ C(12,10)： 66
[(0, 0, 10),
 (0, 1, 9),
 (0, 2, 8),
 (0, 3, 7),
 (0, 4, 6),
 (0, 5, 5),
 (0, 6, 4),
 ・
・
 
 (8, 2, 0),
 (9, 0, 1),
 (9, 1, 0),
 (10, 0, 0)]

7.　重複順列と同じように変数$x_1,x_2$の順に0から9までの整数を順次タプルに追加し、作成途中の組み合わせを作成します。

9.　作成途中の組み合わせで合計がn=10を超えて解になりえないものは除いて、最終的に解となる可能性のあるもののみsolution_listに追加します。

15. $x_3$（最後の要素）は、作成途中の組み合わせの合計とn=10の差を追加して解を完成します。

組み合わせは66通りになり、${}_ 3H_{10}={}_{12} C_{10}=66$から計算した結果と一致します。まとめると次の式で計算することができます。

Equation 2.1　制約なしの不定方程式の解の個数

$\sum\limits_{i=1}^k x_i=x_1+x_2+\cdots+x_k=n\quad0\leqq x_i\leqq n\;(i=1,2,\cdots,k)$
${}_k H_n = {}_{n+k-1} C_n={}_ {n+k-1} C_{k-1}$

全射の場合

前項では解に０が含まれてもより制約なしの条件で計算しましたが、今度は$x_i>=1$なので全射の条件で計算します。上記のプログラムとの変更点は次の2点だけです。

①$x_i$の候補として制約なしの場合は0からとしたものを、全射としたので最小値を1に変更します。また、最大値はn-k+1となります。

②途中に候補としてsolution_listに追加する前のチェックとして、これまでの要素の合計がnと等しくなった時点で最後の要素が０になってしまうので全射の条件を満たすことができません。このため≦を＜に変更します。なお、②の変更は必ずしも必要はありません。

Example 2.2

次の条件を満たす$x_1,x_2,x_3$の組み合わせの数を計算してください。

$x_1+x_2+x_3=10\quad(x_i\geqq1)$

条件が増えて難しそうですが、少しのプログラムの変更で機能を実現することができます。プログラム名は全射の意味を込めてsolve_surjective_equationとします。

Code 2.4　重複組み合わせから全射の不定方程式を解く

  1. def solve_surjective_equation(k, n):
  2. solution_list = [()]
  3. for kth in range(k):
  4. temp = solution_list
  5. solution_list = []
  6. for elm in temp:
  7. if kth < k - 1:
  8. for nth in range(1, n - k + 2): # range(n+1)
  9. if sum(new_elm:=elm + (nth,)) < n: #<=
  10. solution_list.append(new_elm)
  11. else:
  12. break
  13. else:
  14. solution_list.append(elm + (n - sum(elm),))
  15. return solution_list
  17. n = 10
  18. k = 3
  19. equation_surjective_list = solve_surjective_equation(k, n)
  20. print(' solve_surjective_equation 関数で生成: ', len(equation_surjective_list))
  21. print('重複組み合わせ H(3,7)：', H(k, n - k),': 組み合わせ C(9,7)：',comb(n - 1, n - k, exact = True))
  22. equation_surjective_list
solve_surjective_equation 関数で生成:  36
重複組み合わせ H(3,7)： 36 : 組み合わせ C(9,7)： 36 [(1, 1, 8),
 (1, 2, 7),
 (1, 3, 6),
 (1, 4, 5),
 (1, 5, 4),
 (1, 6, 3),
 (1, 7, 2),
 ・
・
 (4, 4, 2),
 (4, 5, 1),
 (5, 1, 4),
 (5, 2, 3),
 (5, 3, 2),
 (5, 4, 1),
 (6, 1, 3),
 (6, 2, 2),
 (6, 3, 1),
 (7, 1, 2),
 (7, 2, 1),
 (8, 1, 1)]

8.　上記①のためrange(n+1)をrange(1, n-k+2)に変更します。

10. 制約なしの場合0が許されるので、途中経過が10以下であれば解になる可能性はありましたが、全射の場合には1以上なのでn以下となります。

${}_3H_{7}={}_{9} C_{2}=36$となります。

制約なしと全射の不定方程式の関係

全射の組み合わせを生成する際に、はじめにk個の$x_i$全てに1ずつを代入し、残りのn-k個のなかで制約なしの不定方程式を解けばよいことになります。このため、制約なしで合計がn-kの不定方程式の解を作成しておき、各$x_i$に1ずつを足すことで全射の組み合わせを生成することができます。

Code 2.5　制約なしと全射の不定方程式を比較する

  1. equation_unrestricted_list = []
  2. for elm in solve_unrestricted_equation(k, n - k):
  3. new_elm = []
  4. for item in elm:
  5. new_elm.append(item + 1)
  6. equation_unrestricted_list.append(tuple(new_elm))
  7. if equation_surjective_list == equation_unrestricted_list:
  8. print('solve_surjective_equation(3, 10) = solve_unrestricted_equation(3, 7) + each 1')
solve_surjective_equation(3, 10) = solve_unrestricted_equation(3, 7) + each 1

2.　引数(k, n-k)で制約なしのsolve_unrestricted_equation関数を呼び出します。

3.　2.の結果の各項目に1を足し込みます。

4.　#15で作成した全射のプログラムの結果と比較します。

結果はTrueということで、両者は一致していることがわかりした。

Equation 2.2　全射の不定方程式の解の個数

$\sum\limits_{i=1}^k x_i=x_1+x_2+\cdots+x_k=n\quad 1\leqq x_i\leqq n-k+1\;(i=1,2,\cdots,k)$
${}_kH_{n-k} = {}_{n-1}C_{n-k}={}_{n-1}C_{k-1}$

合計がnよりも小さくてもよい場合の不定不等式

k個の変数の合計がn以下であるような不等式（制約なし）

次からは応用編です。今度はぴったり10という方程式ではなく、10以下という不等式とします。不定不等式という方はあまりされていないので、とりあえずinequalityとしておきます。

Example 2.3

次の条件を満たす$x_1,x_2,x_3$の組み合わせの数を計算してください。

$x_1+x_2+x_3 \leqq10\quad(x_i\geqq0)$

合計が10だけでなく0から9までも含めて考える必要があるので難しいような気もしますが、不定方程式では$x_0$から$x_{k-2}$までと$x_{k-1}$とで処理を変える必要がありましたが、不等式ではすべてn以下であれば配列に追加する処理でよいので却って単純です。プログラムにおいては不定方程式次のように不等式を等式に書き換えると簡単に計算することができます。ここでは、$k_3$を追加するところで、10ぴったりでなく10以下にすればよいわけです。

関数名は制約なしの不等式という意味でsolve_unrestricted_inequalityとします。

Code 2.6　重複組み合わせから制約なしの不定方程式を解く

  1. def solve_unrestricted_inequality(k, n):
  2. solution_list = [()]
  3. for kth in range(k):
  4. temp = solution_list
  5. solution_list = []
  6. for elm in temp:
  7. for nth in range(n + 1):
  8. if sum(new_elm := elm + (nth,)) <= n:
  9. solution_list.append(new_elm)
  10. else:
  11. break
  12. return solution_list
  14. k = 3
  15. n = 10
  16. inequality_unrestricted_list = solve_unrestricted_inequality(k, n)
  17. print('solve_unrestricted_inequality 関数で生成: ', len(inequality_unrestricted_list))
  18. print('重複組み合わせ H(4, 10)：', H(k +1 , n),': 組み合わせ C(13, 10)：',comb(n + k, n, exact = True))
  19. inequality_unrestricted_list
solve_unrestricted_inequality 関数で生成:  286
重複組み合わせ H(4, 10)： 286 : 組み合わせ C(13, 10)： 286
[(0, 0, 0),
 (0, 0, 1),
 (0, 0, 2),
 (0, 0, 3),
 (0, 0, 4),
 (0, 0, 5),
 (0, 0, 6),
 (0, 0, 7),
 (0, 0, 8),
 (0, 0, 9),

(10, 0, 0)]

9.　とにかく合計がn以下であればリストに追加できます。これは、最後の$x_k$の場合も同じです。

結果的には不定方程式のプログラムより単純になりますが、似たようなものをたくさん作ると混乱してきます。そこで、不定不等式を不定方程式から導く方法を考えます。

$x_1+x_2+\cdots + x_k \leqq n \ x_i\geqq 0\quad(i=1,2,\cdots,k)$

この不等式は、最後に正の整数wを付け加えることにより方程式とみなすことができます。このように不等式を方程式に置き換えるためのwをスラック変数といいます。スラック変数にnと$k_i$の合計との差を表します。

$x_1+x_2+\cdots + x_k +w= n \ x_i\geqq 0\quad(i=1,2,\cdots,k)$

この結果、個数の計算においてはk+1個の正の整数の合計がnになるような組み合わせを見つければよいことになります。そこで、制約なしの不定方程式の解を生成し、配列の右端の要素を切り捨てることにより不等式の解を生成してみます。

Code 2.7　スラック変数を使い不等式を方程式に変換して解を生成する

  1. equation_unrestricted_list = []
  2. for elm in solve_unrestricted_equation(k + 1, n):
  3. new_elm = []
  4. for item in elm:
  5. new_elm.append(item )
  6. equation_unrestricted_list.append(tuple(new_elm[:k]))
  7. if inequality_unrestricted_list == equation_unrestricted_list:
  8. print('solve_unrestricted_inequality(3, 10) = solve_unrestricted_equation(4, 10)[:k]')
solve_unrestricted_inequality(3, 10) = solve_unrestricted_equation(4, 10)[:k]

2.　引数(k+1, n)で制約なしのsolve_unrestricted_equation関数を呼び出します。+1はスラック変数wを指します。

3.　2.の結果の各項目、wを右端に含んだ配列が返されるので、k番目までをスライスすることによりに右端を切り捨てます。

4.　#17で作成した全射のプログラムの結果と比較します。

kを1つ増やして最後の値を切り捨てるだけで方程式が不等式に変化します。このことから次のことがわかります。

Equation 2.3　制約なしの不定不等式の個数

$\sum\limits_{i=1}^k x_i=x_1+x_2+\cdots+x_k\leqq n\quad 0\leqq x_i\leqq n\;(i=1,2,\cdots,k)$
$\sum\limits_{i=1}^k x_i+w=x_1+x_2+\cdots+x_k+w= n\quad 0\leqq w\leqq n$
${}_{k+1}H_{n} = {}_{n+k}C_n= {}_{n+k}C_{k}$

k個の変数の合計がn以下であるような不等式（全射）

最後に、不等式で全射の場合の組み合わせを生成します。$x_i\geqq1)$

Example 2.4

次の条件を満たす$x_1,x_2,x_3$の組み合わせの数を計算してください。

$x_1+x_2+x_3 \leqq10\quad(x_i\geqq1)$

#7を変更して解を生成するプログラムを作成します。全射の不等式という意味でsolve_surjective_inequalityとします。

Code 2.8　全射の不等式の解を生成する

  1. def solve_surjective_inequality(k, n):
  2. solution_list = [()]
  3. for kth in range(k):
  4. temp = solution_list
  5. solution_list = []
  6. for elm in temp:
  7. for nth in range(1, n - k + 2):
  8. if sum(new_elm:=elm + (nth,)) <= n:
  9. solution_list.append(new_elm)
  10. else:
  11. break
  12. return solution_list
  13. k = 3
  14. n = 10
  16. inequality_surjective_list = solve_surjective_inequality(k, n)
  17. print('solve_surjective_inequality 関数で生成: ', len(inequality_surjective_list))
  18. print('重複組み合わせ H(4, 7)：', H(k + 1 , n),' 組み合わせ C(10, 3)：',comb(n + k, n, exact = True))
  19. inequality_surjective_list
solve_surjective_inequality 関数で生成:  120
重複組み合わせ H(4, 7)： 286   組み合わせ C(10, 3)： 286
[(1, 1, 1),
 (1, 1, 2),
 (1, 1, 3),
 (1, 1, 4),
 ・
・
 
 (7, 1, 2),
 (7, 2, 1),
 (8, 1, 1)]

7.　#7との違いは$x_i$を0からではなく1からはじめます。n+1としてn番目まで探しても結果は変わりませんが、なのでn-k+2とします。

最後に制約なしの方程式から全射の不等式を生成します。

制約なしの方程式で生成した組み合わせから、全射の不等式を生成します。このため、制約なしを全射に変更するためn-kの不定方程式の解を作成しておき、各$x_i$に1ずつを足すとともに、kを1つ増やしてスラック変数を切り捨てる処理を組み合わせます。2つを同時にすることでうまくいくか確認します。

Code 2.9　制約なしの方程式で生成した組み合わせから、全射の不等式の解を生成

  1. equation_unrestricted_list = []
  2. for elm in solve_unrestricted_equation(k + 1, n - k):
  3. new_elm = []
  4. for item in elm:
  5. new_elm.append(item + 1)
  6. equation_unrestricted_list.append(tuple(new_elm[:k]))
  8. inequality_surjective_list == equation_unrestricted_list
  9. if inequality_surjective_list == equation_unrestricted_list:
  10. print(' solve_surjective_inequality(3, 10) = solve_unrestricted_equation(4, 7) + each 1')
solve_surjective_inequality(3, 10) = solve_unrestricted_equation(4, 7) + each 1

2.　 solve_unrestricted_equatio関数を呼び出すときに、スラック変数のk+1と全射のn-kを組み合わせます。

3.　全射にするため各$x_i$に1を加えるとともに、右端のスラック変数を切り捨てます。

2つの処理を加えても、お互いに邪魔することなく正しく配列を生成することができました。

Equation 2.4　全射の不定不等式の個数

$\sum\limits_{i=1}^k x_i=x_1+x_2+\cdots+x_k\leqq n \quad1\leqq x_i\leqq n-k+1\;(i=1,2,\cdots,k)$
$\sum\limits_{i=1}^k x_i+w=x_1+x_2+\cdots+x_k+w=n\quad 0\leqq w\leqq n-k$
${}_{k+1}H_{n-k}={}_nC_{n-k}={}_nC_{k}$

全射の不等式の個数

K個からn個を選ぶ組み合わせは${}_kC_n$個であるのに対し、不等式はkとnが反転して${}_nC_k$個になります。不思議に思われるので、n=10,k=3を例に図に表します。

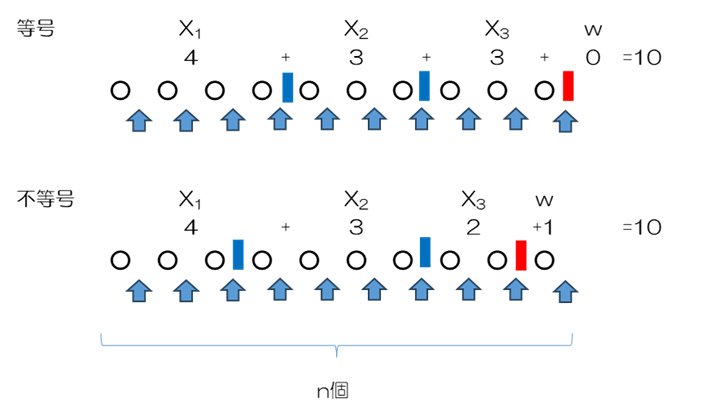
Figure 2.2　全射の不等式
全射の不等式

k=3なので不定方程式であれば、「しきり」は2つで済みますが、不等式なので$x_k$とスラック変数を区切る「しきり」が1つ必要になるので結果的にk個になります。一方、ボールとボールの間隔は、全射の場合は両端を含まないので9個で済みますが、不等式の場合には右端に1つ追加します。変数の合計が10に等しくなる等号の場合には最後の「しきり」が右端に来ます。これに対して、合計が9になる不等号では、右から2番目において、それ以降はスラック変数1となります。このため、結果的にはn(10)個からk(3)個を選べばよいことになります。

不定方程式、不等式のまとめ

不定方程式をまとめ、シンプルなsolve_diophantineという関数名します。4つのパターンの要素を入れ込むと複雑になるので中でsolve_unrestricted_equation関数を呼び出し パターンに応じ必要な変換をします。変数leqは不等式の場合にはTrueとします。通常は方程式なのでデフォルトはFalseとします。

Code 2.10　組み合わせの関数のまとめ

  1. def solve_diophantine(k, n, option='u',leq=False):
  2. if option == 's':
  3. n-=k
  4. if leq == True:
  5. k+=1
  6. l = solve_unrestricted_equation(k, n)
  7. if leq == True:
  8. l=[elm[:-1] for elm in l]
  9. if option == 's':
  10. return [tuple([item+1 for item in elm]) for elm in l]
  11. else:
  12. return [tuple([item for item in elm]) for elm in l]
  14. print(len(solve_diophantine(3,10,option = 'u')))
  15. print(len(solve_diophantine(3,10,option = 's')))
  16. print(len(solve_diophantine(3,10,option = 'u', leq=True)))
  17. print(len(solve_diophantine(3,10,option = 's', leq=True)))
66
36
286
120

2.　あらかじめ各変数kに1を割り振ることにより全射を実現するため、n-k個の中で重複組み合わせを計算します。

4.　leq=True、つまり変数の合計がn未満も許す場合はkとは別にスラック変数wを想定すればよいのでkを1つ追加します。

6.　2から6で設定したn,kをもとにsolve_unrestricted_equation関数を呼び出します。

7.　不等号の場合は、最後のスラック関数は不要なので取り除く処理をします。

リストをタプルに変換して返り値とします。このとき全射にするため2～3.で各変数のためにとっておいた１を足し込んでいきます。

関数を中に関数をつくると、シンプルにすることができます。また、solve_unrestricted_equation関数のような元となる関数をしっかりと作り込んでいけば、後から機能を追加することもできるし、その関数の処理をより効率的にできるとしたら、全ての機能において効率化が図れるので非常に有効といえます。

ictsr4 All Rights Reserved.