組合せ、重複組み合わせ（N:ラベルなし k:ラベルあり）　

多項定理と重複要素を含む順列の生成

多項定理を組み合わせの考え方からとらえる

多項定理と重複要素を含む順列の生成はは前章で取り上げましたが、組み合わせの考え方を使うと、効率的に計算することができるので再度取り上げます。

問題8

青いボールが3個、赤いボールが2個、緑色のボールが2個あります。これらの7個上ボールを一列に並べると、その組み合わせは何通りになりますか。ただし、青、赤、緑のボールはそれぞれ区別しないものとします。

順列の問題ですが、7個のボールを置く場所に0から6まで番号を、それぞれの色が何番目に場所を選ぶかを考えることにより組み合わせの問題に変換します。

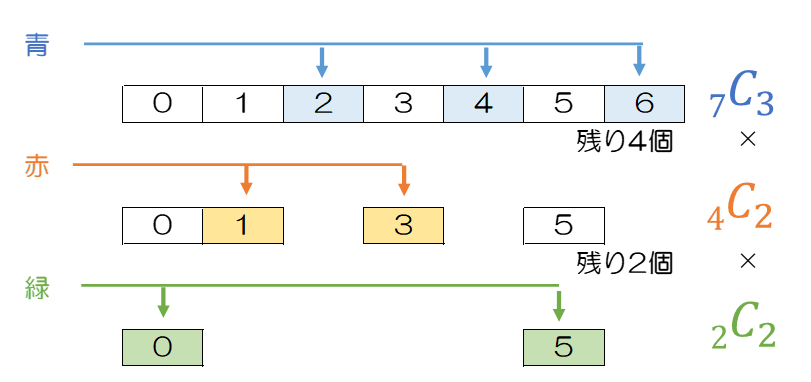
組み合わせによる重複要素を含む順列
組み合わせによる重複要素を含む順列

図のように0から6の7か所に対して、青いボールを置く場所は3か所になるので$ _7C_{3}=35$通りになります。つぎに、35通りに対し、赤いボールを置く場所は残りの4か所のうち2か所になるので$ _4C_{2}=6$通りになります。最後に、残りの白いボール2個は2か所に置くことになるというより、選択の余地が無いので$ _4C_{2}=1$通りになります。つまり、$35\times 6\times1=210$通りになります。

一般化すると、p個、q個、r個の計n個のボールを一列に並べる際の組み合わせは、次のように計算します。

$n=p+q+r$

$ _n C_p\times _{n-p} C _q\times _{n-p-q} C _r$

$\displaystyle= \frac{n!}{p!(n-p)!}\times\frac{(n-p)!}{q!(n-p-q)!}\times\frac{(n-p-q)!}{r!(n-p-q-r)!}$

$\displaystyle= \frac{n!}{p!q!r!(n-p-q-r)!}=\frac{n!}{p!q!r!}$

$\because(n-p-q-r)!=0!=1$

この計算は、色の数が3よりも大きくなっても、同じように約分できるので次のように計算することができます。最終的には、前章での順列による方法から導いた数式と一致します。

数式2-10 多項定理の個数の計算

m種類のボールがそれぞれ$p_k$個、合計n個あるときの多項定理の数

$\displaystyle\frac{n!}{{p_{1}!\cdot p_{2}!\cdot p_{3}!\cdots p_{m}!}}=\frac{n!}{\prod\limits_{k=1}^m p_k!}$

$\sum\limits_{k=1}^m p_k=n$

組み合わせを使い重複要素を含む順列を生成する

選ばれる要素と選ばれない要素を分離する

組み合わせを使い重複要素を含む順列の生成するためには、ある色が決められた個数の場所を選んだら、次の色が残った色からさらに場所を選ぶ必要があります。そこで、組合せを生成する関数を改良し、配列から選ばれる要素と選ばれない要素を分割する必要があります。例えば、[(0,1,2,3,4,5)]から(0,1)が選ばれた場合、[(0,1)(2,3,4,5)]のように分割します。そこで、関数名を組み合わせの残りという意味でcomb_resudial_func とし、分割する配列を(0,1,2,3,4,5)、選ばれる要素数（ここでは2）をnを引数とします。またプログラムをすっきりさせるために、comb_injective_funcを使うのであらかじめ実行しておく必要があります。引数として、選ぶ前のリストoriginalと選ぶ数selected_nを渡し、戻り値として選ばれた組み合わせと選ばれなかった組み合わせを1つの要素の配列を返します。

組み合わせの配列で選ばれなかった要素も入れ込む

  1. def comb_remaining_func(original, selected_n):
  2. array = []
  3. for comb_elm in comb_injective_func(original, selected_n):
  4. remaining = []
  5. for item in original:
  6. if item not in comb_elm:
  7. remaining.append(item)
  8. array.append([comb_elm, tuple(remaining)])
  9. return array
  11. original = range(7)
  12. selected_n = 2
  13. comb_remaining_func(original, selected_n)
[[(0, 1), (2, 3, 4)],
 [(0, 2), (1, 3, 4)],
 [(0, 3), (1, 2, 4)],
 [(0, 4), (1, 2, 3)],
 [(1, 2), (0, 3, 4)],
 [(1, 3), (0, 2, 4)],
 [(1, 4), (0, 2, 3)],
 [(2, 3), (0, 1, 4)],
 [(2, 4), (0, 1, 3)],
 [(3, 4), (0, 1, 2)]]

3.　comb_injective_func関数で生成した組み合わせの組み合わせを1つずつcomb_elmとして取り出します。

5.　選ばれるまでのoriginalに対して、3.で取り出した組み合わせの中で、comb_elmにない要素が選ばれなかったものになるので、remainingに追加します。

8　選ばれたcomb_elmと選ばれなかったremainingをまとめてarrayに追加します。このときremainingはcomb_listに合わせてタプルに変換します。

重複要素を含む順列の並び順を決める

赤3個、青2個、白1個であれば、辞書dictとして[青:3, 赤:2, 緑:2]というリストを引数として渡します。重複要素を含む順列にするために、青いボールが何番目と何番目に置き、次に赤いボールを何番目と何番目に置き、残った場所に白ボールを置くというような並び順の配列を生成します。つまり、 リストの左側から青、赤、緑がおかれる場所を[(0, 1, 2), (3, 4), (5, 6)]のようなリストを作成し、このリストから[青,青,青,赤,赤,緑,緑]となるように変換します。にここではcomb_ remaining func関数を早速使用し、その中でcomb_injective_funcを使うのであらかじめ実行しておく必要があります。

重複要素を含む順列を生成する

  1. def multinominal_func(dict):
  2. k_list=list(dict.keys())
  3. n_list=list(dict.values())
  4. n=sum(n_list)
  5. seq_array = [[tuple(range(n))]]
  6. for i in range(len(n_list) - 1):
  7. temp =seq_array
  8. seq_array = []
  9. for elm in temp:
  10. for item in comb_remaining_func( (elm[-1], n_list[i]):
  11. seq_array.append(elm[:-1] + item)
  12. array=[]
  13. for elm in seq_array:
  14. new_elm = [''] * n
  15. for i,item in enumerate(elm):
  16. for num in item:
  17. new_elm[num] = k_list[i]
  18. array.append(tuple(new_elm))
  19. return array
  20. dict = {'青':2, '赤':3, '緑':2}
  21. multinominal_func(dict),len(multinominal_func(dict))
[('青', '青', '青', '赤', '赤', '緑', '緑'),
 ('青', '青', '青', '赤', '緑', '赤', '緑'),
 ('青', '青', '青', '赤', '緑', '緑', '赤'),
 ('青', '青', '青', '緑', '赤', '赤', '緑'),
 ('青', '青', '青', '緑', '赤', '緑', '赤'),
 ('青', '青', '青', '緑', '緑', '赤', '赤'),
 ('青', '青', '赤', '青', '赤', '緑', '緑'),
 ('青', '青', '赤', '青', '緑', '赤', '緑'),

2.　dictとして[青:3, 赤:2, 緑:2]に対して、keys（色:青、赤、緑）をk_list代入します。

3.　同様にdictからvalues(個数,3,2,2)をn_listに代入し4.でその個数をnに代入します。

5.　seq_arrayに①の配列を生成するため、要素数が7の場合、[[(0, 1, 2, 3, 4, 5, 6)]]のように2重のリストに0～6の数字を並べたタプルが入るような配列を作成します。

7.　seq_arrayの中身をいったんtempに代入したのち初期化し、8.でseq_arrayに元の組み合わせ対してcomb_remaining_func関数を使い選ばれた色と選ばれなかった色に分けます。

14. seq_arrayに対し②の組み合わせをarrayに生成します。順列の要素数7の場所を確保し初期化します。

15. seq_arrayの要素を読み込んだら、初めに0番目の要素青の場所が[0,1,2]に青を代入します。同様に赤、緑の場所に代入していきます。

重複要素を含む順列のプログラムの効率を比較する

前章では順列から重複要素を含む順列を絞りこんで作成しましたが、効率が良くないことを指摘しました。一方、ここでは組み合わせで順番を決める方法で作成しました。そこで両者を同じ条件で実行し、時間を計測します。時間計測はtimeitモジュールのtimeit関数を使用します。

Timeit関数で時間計測をする

  1. import timeit
  2. loop = 500
  3. result = timeit.timeit('multinominal_func2(dict)', globals=globals(), number=loop)
  4. print(result / loop)
0.000678211000000374

3.　timeitモジュールは変数や関数を独自に名前空間を作りますが、globals=globals()を指定するとまた、numberパラメータで実行回数を指定します。

4.　resultに関数の結果として計算した500回の実行時間が代入されるので、これを実行回数500で割って、1回あたりの実行時間を計算します。

ictsr4 All Rights Reserved.