スターリング数　Nラベルあり Kラベルなし　全射

スターリング数について理解するため、次の問題を考えます。

Example 3.1

出席番号0から5までの6人を4台のタクシーに分乗し、市内を観光します。タクシーは区別しない（ラベルなし）とすると、考えられる組み合わせは何通りになりますか。なお、各タクシーには少なくとも1人は乗るものとします。

第1章ではラベルのある学生を区別のある部屋へ割り当てることを例に取り、重複順列について検討しました。一方、この章ではラベルのある（labeled）部屋をラベルのない(unlabeled)タクシーに置き換え、グループ分けだけに集中します。このような組み合わせの数はスターリング数と呼ばれ、これにもとづく組み合わせはスターリング数に対応する集合分割（set partition）といいます。なお、今後は簡便のため「集合分割」と呼ぶことにします。

全射の重複順列からスターリング数に対応する集合分割を生成

写像から見たスターリング数と集合分割

重複順列では定義域の集合Nから値域の集合Kへの写像で、いずれの集合ともにラベルありで順列の生成と個数の計算を行いました。一方、重複組み合わせでは集合Nの要素をラベルなしにするため、増加写像の考え方を使い、集合Kの要素が昇順になるような組み合わせに絞り込みました。これに対し、スターリング数では、集合Nはラベルあり、集合Kはラベルなしの組み合わせを考えます。このため、集合Nの要素が昇順になるような組み合わせに絞り込むことが必要となります。

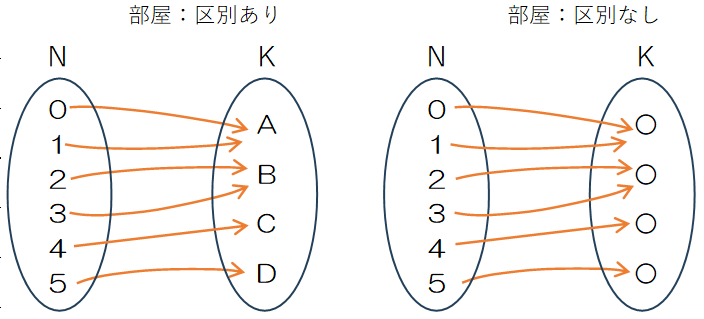
Figure 3.1　重複順列と重複組み合わせと集合分割との相違
重複順列と重複組み合わせと集合分割との相違

集合Kについてラベルなしにする前の重複順列の例を挙げるとFigure 3.2のようになります。

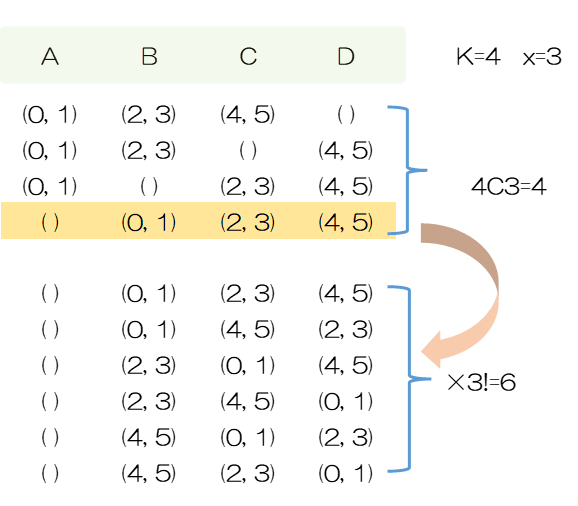
Figure 3.2　集合Kを基準に集合分割を整理
集合Kを基準に集合分割を整理

2つの重複順列は別のものとして数えますが、集合Kのラベルがない構造に変換するとA, B, C, Dの区別がなくなるので、(0, 1), (2,3), (4), (5)の組み合わせでそれぞれ1台のタクシーに乗るので同じ集合分割になります。とはいえ、それらを同じ集合分割として捉えるのは容易ではありません。そこで、視点を変え、A, B, C, Dの4つのタクシーにだれが乗るか、という視点でリストを変換するinverse_value_mapping関数を作成します。Figure 3.3で示すように、新たなリストnew_elmにk_listの要素の数だけ各タクシーに対応する空のリストを初期化し、A→0、B→1、C→2、D→3という対応にして、リストの添え字にします。そして、それぞれの重複順列の要素について、例えば出席番号2の学生がAの車に乗るとしたら、new_elm[0]に2を追加します。こうすることにより、どのタクシーにどの学生の組み合わせが乗るのかが明らかになります。

次に、増加関数の考え方を使い昇順に並んでいるものに絞り込みます。これについては以前作成したfilter_increasing_map関数を使用します。

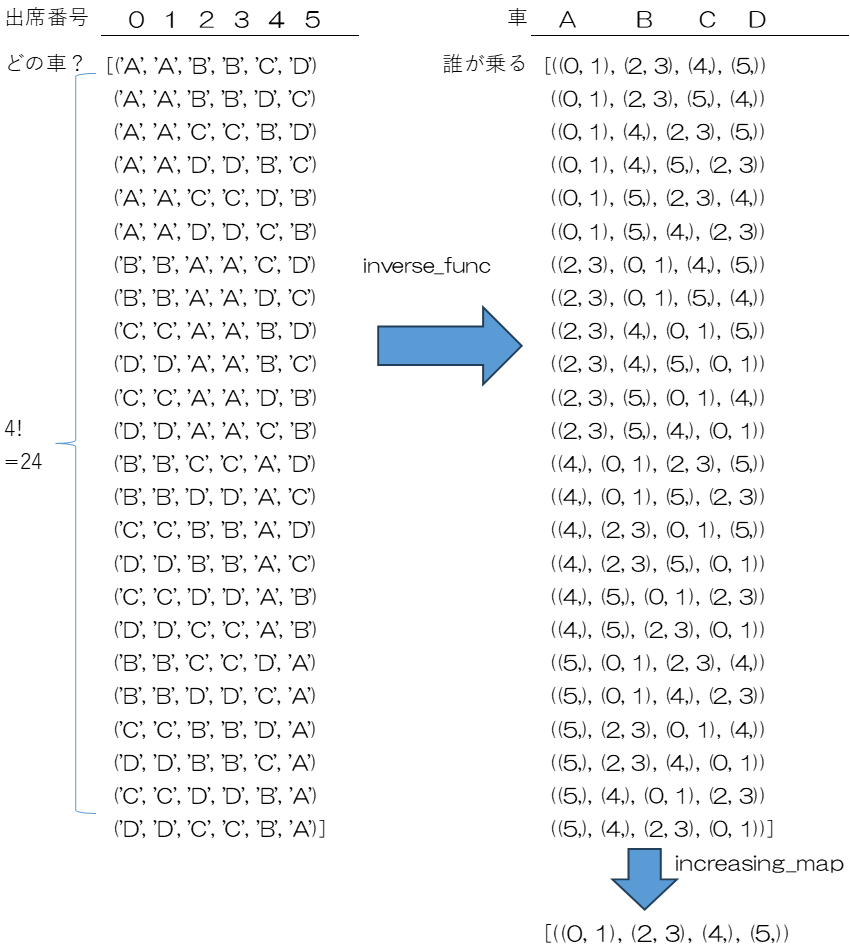
Figure 3.3　集合Kについてラベルなしの構造に変換
集合Kについてラベルなしの構造に変換

右側の配列にすると、重複組み合わせに対し集合Kについてラベルが無い構造に変換すると全て同じ組み合わせになります。k=4なので第2階層の要素数4のタプルについての順列、$k!=4!=24$個が1つに集約されることがわかります。

ラベルありの全射の重複順列の生成

全射の重複順列はp90111で作成したgenerate_surjective_perm関数を使い、全射の重複順列から抜き出したリストsurjective_perm_listを生成します。このため、関数の実行に当たりgenerate_surjective_perm関数を使い一度実行しておく必要があります。

Code 3.1　全射の重複組み合わせを生成

  1. k_list = ['A', 'B', 'C', 'D']
  2. k = len(k_list)
  3. n = 6
  4. surjective_perm_list = generate_surjective_perm(k_list, n)
  5. print(
  6. f'generate_surjective_perm({len(k_list)}, {n}) = '
  7. f'{len(surjective_perm_list)}'
  8. )
  9. surjective_perm_list
generate_surjective_perm(4, 6) = 1560
[('A', 'A', 'A', 'B', 'C', 'D'),
 ('A', 'A', 'A', 'B', 'D', 'C'),
 ('A', 'A', 'A', 'C', 'B', 'D'),
 ('A', 'A', 'A', 'C', 'D', 'B'),
・
('A', 'A', 'B', 'B', 'D', 'C'),
・
('B', 'B', 'A', 'A', 'D', 'C'),
・
('D', 'D', 'D', 'B', 'C', 'A'),
 ('D', 'D', 'D', 'C', 'A', 'B'),
 ('D', 'D', 'D', 'C', 'B', 'A')]

1.　実例に副ってプログラムを作成し実行するため、集合Kをリストk_list=['A', 'B', 'C', 'D']と定義し、今後、要素数を計算に使うことも多いのでkにはkリストの要素数、4を代入します。

2.　生成した全射の重複順列を出力しますが、1560通りと膨大な数になるので一部の表示に留めます。

全射の重複順列は、前章で次のような包除原理を使った計算式で求めることができます。

Equation 3.1　包除原理を使った全射の重複順列の個数

$PIE(n, k)=\sum\limits_{i=0}^{k}(-1)^i\,{}_kC_i(k-i)^n$

さっそく、第1章で作成したcalc_surjective_perm関数を使い全射の重複順列の数を計算します。

Code 3.2　重複順列の全射の公式を使って個数を計算（再掲）

  1. print(
  2. f'calc_surjective_perm({len(k_list)}, {n}) = '
  3. f'{calc_surjective_perm(n, len(k_list))}'
  4. )
count_surjective_perm(4, 6) =  1560

7.　Code 3.1と比較するため、k = 4、n = 6を引数として渡します。

Code 3.1で得られた1560通りという結果と一致していることが確認できました。

重複順列を集合Nについてラベルがない構造に変換

全射の重複順列を生成する

全射の重複順列では集合Kを基準に増加関数の考え方を適用するのが困難なので、視点を変えて、どのタクシーにどの学生が乗るかを示す集合分割を生成する関数を作成します。関数名は値の配列を逆にするという意味でinverse_value_mapping関数と命名し生成するリストをinverse_value_mapping_listとします。inverse_value_mapping_listの中の1つの重複順列をnew_elmとし、k_listの要素数のタプルで構成されます。perm_listから読み込んだ要素itemの集合Kでの順序を示す値をインデックスとしてnew_elmの該当するタプルに追加します。この際、リストk_listにindexメソッドを適用します。例えばk_list = ['A', 'B', 'C', 'D']に対して、k_list.index(‘C’)に対して‘C’のk_listにおけるインデックス（0から始まる順序）を返します。

Code 3.3　集合Kの要素を基準に重複順列を整理

  1. def inverse_value_mapping(k_list, perm_list):
  2. converted_list = []
  3. for elm in perm_list:
  4. new_elm = [() for _ in range(len(k_list))]
  5. for num, item in enumerate(elm):
  6. new_elm[k_list.index(item)] += (num,)
  7. converted_list.append(tuple(new_elm))
  8. return converted_list
  10. inverse_value_list = inverse_value_mapping(
  11. k_list,
  12. surjective_perm_list
  13. )
  14. print(f'inverse_value_list = {len(inverse_value_list)}')
  15. inverse_value_list
calc_surjective_perm(4, 6) = 1560
[((0, 1, 2), (3,), (4,), (5,)),
 ((0, 1, 2), (3,), (5,), (4,)),
 ((0, 1, 2), (4,), (3,), (5,)),
 ((0, 1, 2), (5,), (3,), (4,)),
・
((0, 1), (2, 3), (4,), (5,)),
・
((2, 3), (0, 1), (5,), (4,)),
・
((5,), (4,), (3,), (0, 1, 2))]

4.　new_elmで、AからDの4台のタクシーに誰が乗るかを表す組み合わせの1つを集計します。このため、k_listの数k=4の空のリストをあらかじめ定義しておきます。初期化をするだけなのでインデックスは必要ないので”for _ in”とします。

6.　例えば、permの要素であるitemのk_listにおける添え字をnew_elmの該当するタプルに追加します。

配列を並べ替えただけなので、まだ、この段階では件数は1560件と変わりません。

集合Kに増加写像を適用しラベルなしの集合分割に変換

集合Kについて増加写像の考え方を使いラベルなしの構造に変換するため、p90120作成したfilter_increasing_map関数を適用します。このことにより( (0, 1), (2, 3), (4), (5))、((0, 1), (2, 3), (5) , (4))、((2, 3), (0, 1), (4), (5))などは、昇順に並んでいる((0, 1), (2, 3), (4), (5))に代表させることにより、ラベルなしの分割に集約することができます。

Code 3.4　増加関数の考え方を使い集合Kをラベルなしの構造に変換

  1. unlabeled_partitions_list = filter_increasing_map(inverse_value_list)
  2. print(f'unlabeled_partitions_list = {len(unlabeled_partitions_list)}')
  3. unlabeled_partitions_list
unlabeled_partitions_list = 65
[((0, 1, 2), (3,), (4,), (5,)),
 ((0, 1, 3), (2,), (4,), (5,)),
 ((0, 1), (2, 3), (4,), (5,)),
 ((0, 1, 4), (2,), (3,), (5,)),
 ((0, 1), (2, 4), (3,), (5,)),
 ((0, 1), (2,), (3, 4), (5,)),
 ((0, 1, 5), (2,), (3,), (4,)),
 
・
・
((0,), (1, 5), (2,), (3, 4)),
 ((0,), (1,), (2, 5), (3, 4)),
 ((0,), (1,), (2,), (3, 4, 5))]

5.　変換された重複順列を1つずつelmとして読みこみ、要素の1番目と2番目、２番目と3番目・・というように次々と大きさを比べます。このとき、後の要素の方が小さい場合は増加写像の要件を満たさなくなるので、対象外となり6.でbreakします。

7.　5～6.に一度もあてはまらずループを抜けたものは増加写像となるので、surjective_listに追加します。

n=4,k=6のスターリング数は、包除原理により求めた全射の重複順列の1560通りをn!=4!=24で割った65通りに絞られました。

スターリング数を計算する関数

前節での検討が正しいかをSymPyライブラリの関数を使い確認し、スターリング数の個数を計算する関数と、集合分割を生成する関数を作成します。

SymPyライブラリのstirling関数を使いスターリング数を計算する

スターリング数の計算にはSymPyライブラリのsympy.functions.combinatorial.numbersモジュールで提供される stirling関数を使用します。stirling関数は集合Nの個数nと集合Kの個数kを引数とします。

Code 3.5　SymPyライブラリのstirling関数によるスターリング数の計算

  1. from sympy.functions.combinatorial.numbers import stirling
  2. print(
  3. f'sympy_stirling({n}, {len(k_list)}) = '
  4. f'{stirling(n, len(k_list))}'
  5. )
sympy_stirling(6, 4) =  65

2.　前節での結果と比べるため、n=6,k=4を引数とします。

65通りとなりとCode 3.4で導いた結果と一致していることがわかりました。

包除原理を使いスターリング数を計算する関数を作成

スターリング数の計算式

スターリング数は、大文字のSを使いS(n, k)とあらわします。スターリング数は包除原理による全射の重複順列の計算式に変更を加えることにより導くことができます。計算式で、kの値ごとに重複順列の個数を計算し加減するところで、ラベルなしの個数にするためk!で割る処理を加えます。

Equation 3.2　スターリング数の計算

$S(n, k)=\sum\limits_{i=0}^{k}(-1)^i\,{}_kC_i(k-i)^n/k!$

スターリング数を計算する関数

スターリング数を計算する関数を作成します。関数名は文字通りcalc_stirling_countとします。なお、組み合わせはcomb関数、階乗はfactorial関数を使用するのでimportあらかじめインポートしておく必要があります。

Code 3.6　スターリング数を計算する関数

  1. def calc_stirling_num(n, k):
  2. sigma = 0
  3. for i in range(k + 1):
  4. sigma += ((-1)**i) * comb(k, i) * (k - i)**n
  5. return int(sigma / factorial(k))
  7. print(
  8. f'calc_stirling_num({n}, {len(k_list)}) = '
  9. f'{calc_stirling_num(n, len(k_list))}'
  10. )
calc_stirling_num(6, 4) =  65

7.　 perm_surjective_counと同じ包除原理を使い、全射の重複順列の個数を計算し、戻り値を返すときに、$k!$で割ります。割り算の結果は小数点型になるので、int関数で整数に変換します。

8.　 Code 3.4の結果と比べるため、n=6,k=4を引数とします。

集合分割を生成する関数

SymPyライブラリのmultiset_partitions関数を使い集合分割を生成

集合分割には、SymPyライブラリのsympy.utilities.iterablesモジュールで提供されるmultiset_partitions関数を使用します。引数としてn,,kを渡しますが、nは集合Nの要素をリストでも個数でも可能です。前節に作成した集合分割と一致するか確認します。multiset_partitionsは集合を指定した数に分割するものですが、集合に同じ値の要素があることも許されます。このため、集合分割は多重分割の特殊なケースと考えられます。

Code 3.7　SymPyライブラリのmultiset_partitionsによる集合分割の生成

  1. from sympy.utilities.iterables import multiset_partitions
  2. sympy_multiset_partitions_list = list(multiset_partitions(n, len(k_list)))
  3. sympy_multiset_partitions_list
[[[0, 1, 2], [3], [4], [5]],
 [[0, 1, 3], [2], [4], [5]],
 [[0, 1], [2, 3], [4], [5]],
 [[0, 1, 4], [2], [3], [5]],
 [[0, 1], [2, 4], [3], [5]],

[[0], [1], [2, 5], [3, 4]],
 [[0], [1], [2], [3, 4, 5]]]

2.　前節での結果と比べるため、n=6,k=4を引数とします。

生成した集合分割とSymPyライブラリの計算結果を比較

集合分割を比較するためリストの形式を変換

重複組み合わせをラベルがない構造に変換すると、全て同じ組み合わせになることがわかります。k=4 なので、第2階層の要素数 4 のタプルについての順列k!=4!=24通りが1つに集約されることがわかります。

リストやタプルのような構造が入れ子になったデータを扱う際には、「階層」というよりも「ネスト（入れ子構造）」という用語が使われます。最上位のリストを第1階層とすれば、リスト内のリスト（あるいはタプル）が第2階層、さらにその内側が第3階層というように、構造が深くなるにつれて階層が増します。

順列や組み合わせを生成する関数では、itertoolsモジュールに合わせて第1階層はリスト、第2階層以降にはタプルとなっている、自作関数においてもそれに合わせています。一方、SymPyライブラリで生成される組み合わせはすべてリストとして出力されるため、両者が一致しているかを確認するには、形式を変換する必要があります。

そこで、最上位の階層はリスト、第2階層以下をすべてタプルに変換する関数を定義します。関数名はconvert_to_tupleとし、ネスト構造の深さに応じて再帰的に処理することで、任意の深さの構造に対応できるようにしています。

Code 3.8　リストをタプルに変換する

  1. def convert_to_tuple(sequence, output='tuple', depth=1):
  2. if isinstance(sequence, (list, tuple)):
  3. temp_list = [convert_to_tuple(item, output, depth + 1)
  4. for item in sequence]
  5. if output == 'list':
  6. return list(temp_list)
  7. else:
  8. if depth == 1:
  9. return list(temp_list)
  10. else:
  11. return tuple(temp_list)
  12. else:
  13. return sequence
  16. print(convert_to_tuple([[1, 2], [[2], [3, 4]], [3]]))
  17. print(convert_to_tuple(((1, 2), ((2,), (3, 4)), (3,))))
  18. print(convert_to_tuple(([1, 2], [(2,), (3, 4)], (3,))))
  19. print(convert_to_tuple([[1, 2], [[2], [3, 4]], [3]],'list'))
  20. print(convert_to_tuple(((1, 2), ((2,), (3, 4)), (3,)),'list'))
  21. print(convert_to_tuple(([1, 2], [(2,), (3, 4)], (3,)),'list')) 
[(1, 2), ((2,), (3, 4)), (3,)]
[(1, 2), ((2,), (3, 4)), (3,)]
[(1, 2), ((2,), (3, 4)), (3,)]

4.　引数 sequence がリストまたはタプルである場合、その中の各要素に対して再帰的にconvert_to_tuple を適用します。その際、現在の深さ depth を1だけ増やすことで、ネスト構造の深さを追跡します。

5.　再帰処理の結果を temp_list に格納し、最上位階層（depth == 1）であればリストとしてそのまま返します。それ以外の深さ（第2階層以下）では、結果をタプルに変換して返します。

6.　この処理により、最上位の構造はリスト、それ以外のすべての入れ子構造はタプルに変換されます。

7.　一方、引数 sequence がリストでもタプルでもない（たとえば整数や文字列などの）通常の値である場合は、それ以上分解する必要がないため、その値をそのまま返します。

前節で生成した集合分割をSymPyライブラリによる結果と比較する

さっそく、SymPyで作成したsympy_multiset_partitions_listと比較します。

Code 3.9　ライブラリの関数と比較

  1. if convert_to_tuple(sympy_multiset_partitions_list) == unlabeled_partitions_list:
  2. print('sympy_multiset_partitions_list == unlabeled_partitions_list')
sympy_multiset_partitions_list == unlabeled_partitions_list

2.　第1階層の各リストについて、タプルに変換します。

multiset_partmultiset_partitions関数で生成したsympy_multiset_partitions_listは、convert_to_tuple関数を使用してunlabeled_partitions_listと同じ形式に変換します。

集合分割を比べます。Code 3.8の計算結果が正しいことを確認することができました。次の節では、スターリング数を簡単に計算する漸化式を作成し、これをもとに集合分割を生成する方法を考えます。

ictsr4 All Rights Reserved.