スターリング数の漸化式

スターリング数の一覧表から漸化式を導く

前節では包除原理を使い生成した全射の重複順列から増加関数の考え方を用いて、スターリング数に対応する集合分割を抜き出しました。SymPyライブラリの関数と比較し正しく計算できることは確認しましたが、もっと切れのよいプログラムを作成したくなります。そこでこの節では、スターリング数に関わる興味深い漸化式を使い導き再帰関数を使い、同じ計算をすることを考えます。

スターリング数の一覧表を作成する

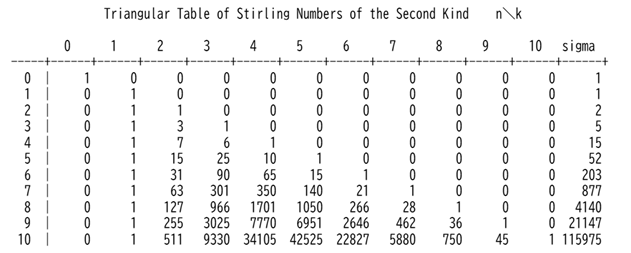
漸化式を作る上でのヒントにするため、SymPyライブラリのsympy.functions.combinatorial.numbersモジュールで提供される stirling関数を使ってn=10までのスターリング数の一覧表を作成します。表の作成に当たっては、今後、同じ処理が必要になることを想定し、print_table関数を定義します。print_table関数は、引数として表示させたい数値を要素とする2階層のリストやタプルと、その数値の桁数に応じた列幅を引数として渡すことにより、リストの添え字と数値一覧表および、各行の合計をsigmaとして表示するように設計します。

Code 3.10　表を作成する関数を作成し、第2種スターリング数の一覧表を作成する

  1. def print_table(array, w):
  2. print(' ' * (w + 2), end='')
  3. for k in range(len(array[0])):
  4. print(f'{k:^{w + 2}}', end=' ')
  5. print('sigma')
  7. print('-' * (w + 1), end='+')
  8. for k in range(len(array[0]) + 1):
  9. print('-' * (w + 2), end='+')
  10. print()
  12. for n in range(len(array)):
  13. print(f'{n:^{w + 1}}', end='|')
  14. sigma = 0
  15. for k in range(len(array[0])):
  16. print(f'{array[n][k]:>{w + 2}}', end=' ')
  17. sigma += array[n][k]
  18. print(f'{sigma:>{w + 2}}')
  20. max_n = 10
  21. max_k = 10
  22. sympy_stirling_table = []
  23. for idx_n in range(max_n + 1):
  24. row = []
  25. for idx_k in range(max_k + 1):
  26. row.append(int(stirling(idx_n, idx_k)))
  27. sympy_stirling_table.append(row)
  28. title = 'Triangular Table of Stirling Numbers of the Second Kind n＼k'
  29. print(title.center(90))
  30. print('')
  31. print_table(sympy_stirling_table, 4)
 第2種スターリング数の一覧表

2.　5.までのコードで、表の1行目のkの値を表示します。print関数でendパラメータを” ”とすることにより改行しないようにすることができます。（このパラメータはデフォルトでは制御記号\nを出力することにより改行するように設定されています。）

6.　9.までで表の2行目の区切り線を表示します。9.でprint関数に何も指定しないことにより改行するようにしています。

10. 16.までで、0から表の行数に応じて各要素の値を表示します。この際、各値をsigmaで合計し、16.で出力します。

20. スターリング数の表を空のリストで定義します。22.でさらに第2階層のリストrowを定義しnの値ごとの値を追加していきます。

24. stirling関数を使い、スターリング数を計算し、リストrowに追加することを繰り返します。

スターリング数の一覧を表示することができました。

スターリング数の漸化式の導出と検証

スターリング数の漸化式の考え方

Code 3.10で作成した表を観察すると、スターリング数には次の3つの特徴があることが読み取れます。漸化式の条件には計算の出発点となる境界条件（boundary conditions） または 初期条件（initial conditions） とそれ以外の再帰関係（recurrence relation）があります。スターリング数の場合次のようになります。

境界条件

① k = 1の場合　$S(n,1) = 1 \quad (n \geq 1)$

n人が1台に乗る場合、分乗する余地もなく1通りしかありません。nがどんなに大きくてもスターリング数は1になります（タクシーの定員は無視すれば）。

② n = kの場合 $S(n,n) = 1 \quad (n \geq 0)$

n人でn台に分乗する場合、1人1台になります。タクシーにラベルがない前提なので、組分けを考える余地はなく、スターリング数は1になります。

再帰関係

③ ①、②以外の場合 $S(n, k) =S(n-1, k-1)+k\; S(n-1, k)$

S(6, 4)、つまり6人で4台のタクシーに分乗する予定にしていました。ところが学生が１人増え、これにともないタクシーを1台増やすとスターリング数はS(7, 5)となります。このS(7, 5)は、新しく来た学生が1人で1台を独占するか、他の学生と同乗するかに分けることができます。

1人で1台を独占する場合、前からいた学生6人がタクシー4台へ分乗するので、S(6, 4)通りと変わりません。一方、他の学生と同乗する場合、前からいた6人を5台に分けておき、新しく来た学生は5台のうちいずれかに乗るものとします。新しい分割の数はS(6, 5)×5になります。つまり、S(7,5)=S(6,4)+S(6,5)×5=65+15×5=140となります。

漸化式が正しいか、1例を取って検証する

前項のスターリング数の漸化式の考え方を、検証します。ここではS(6, 4)S(6, 5)およびS(7, 5)を例にとりSymPyライブラリのstirling関数を使って計算します。

Code 3.11　漸化式でスターリング数を計算

  1. n = 7
  2. k = 5
  3. print(f'S({n - 1}, {k - 1}) = {stirling(n - 1, k - 1)}')
  4. print(f'S({n - 1}, {k}) = {stirling(n - 1, k)}')
  5. print(f'S({n}, {k}) = {stirling(n, k)}')
  6. result = stirling(n - 1, k - 1) + k * stirling(n - 1, k)
  7. print(f'S({n - 1}, {k - 1}) + {k} × S({n - 1}, {k}) = {result}')
S(6, 4)= 65  S(6, 5)=15
S(7, 5)=140
S(6, 4)+5×S(6, 5)=140

3.　1.で計算したいことを確認します。

漸化式の考え方が正しいことが確認できました。スターリング数の漸化式は次のようになります。しかし、ここで表を再度見るとS(0,0)=1となっていることに目を向けます。するとこれまでの境界条件では耐えられないので、新たな条件を設けます。

Equation 3.3　スターリング数の漸化式

境界条件１

① $S(n,1) = 1 \quad (n \geq 1)$

② $S(n,n) = 1 \quad (n \geq 0)$

境界条件２

$S(0,0) = 1 \quad$ \
$S(n,0) = 0 \quad (n \geq 1)$ \
$S(0,k) = 0 \quad (k \geq 1)$

再帰関係

③ $S(n, k) =S(n-1, k-1)+k\; S(n-1, k)$

プログラムを作成するうえでは、実務的にはnや kが0になるようなケースは考えずられず、プログラムの実行回数が少ないので境界条件１の方が良くなりますが、境界条件２の方が今後の発展的な議論を踏まえると応用が利くのでここでは後者を使ってプログラムを作成します。

漸化式によりスターリング数を計算し、集合分割を生成する

漸化式を使ってスターリング数を計算する関数

漸化式をもとにスターリング数を求めるcalc_stirling_num_recursive関数を作成し、S(7, 5)を計算します。再帰関数とするので、functools モジュールから lru_cache デコレータをインポートし適用します。@lru_cache デコレータは、再帰呼び出しで同じ引数の組み合わせが何度も現れるこの関数では計算結果を記憶し、再計算することを防ぐことにより実行時間を大幅に短縮できます。このように、データを一時的に保存しておくことをキャッシュ化といい、特に再帰関数の実行結果を一時的保存しておくことをメモ化といいます。

Code 3.12　漸化式を使ったスターリング数の計算

  1. @lru_cache
  2. def calc_stirling_num_recursive(n, k):
  3. if k == 0 and n == 0:
  4. return 1
  5. if k == 0 or n == 0:
  6. return 0
  7. return (
  8. calc_stirling_num_recursive(n - 1, k - 1)
  9. + k * calc_stirling_num_recursive(n - 1, k)
  10. )
  12. n = 7
  13. k = 5
  14. print(f'S({n}, {k}) = {calc_stirling_num_recursive(n, k)}')
S(7, 5) = 140

2.　 lru_cacheデコレータ関数を定義する前の行で@マークを付けて指定します。

4.　漸化式①、②に対応する部分で、再帰的にプログラムを呼び出すことなくreturnを返します。

6.　漸化式③の左辺$S(n-1, k-1)$に対応します。nとkを1つずつ減らしながら次々と再帰するので、k=1となったところで3.に入り1を返します。

7.　漸化式③の右辺$S(n-1, k)$に対応します右片はnだけを1つずつ減らしながら再帰するので、n=kとなった時点で3.に入り1を返します。

$S(7, 5)=140$と正しく計算することができました。漸化式をもとに再帰関数を作成すると、簡単なプログラムでスターリング数を計算することができます。さらに、次にcalc_stirling_num_recursive関数を使い、スターリング数の一覧を作成します。

Code 3.13　再帰関数によるスターリング数の一覧の計算

  1. sigma_hits = 0
  2. sigma_misses = 0
  3. recursive_stirling_table = [
  4. [0 for _ in range(max_k + 1)]
  5. for _ in range(max_n + 1)
  6. ]
  7. for idx_n in range(max_n + 1):
  8. for idx_k in range(max_k + 1):
  9. value = calc_stirling_num_recursive(idx_n, idx_k)
  10. recursive_stirling_table[idx_n][idx_k] = value
  11. cache_info = calc_stirling_num_recursive.cache_info()
  12. sigma_hits += cache_info.hits
  13. sigma_misses += cache_info.misses
  14. if recursive_stirling_table == sympy_stirling_table:
  15. print('calc_stirling_num_recursive == sympy_stirling' )
  16. print('sigma_hits = ',sigma_hits)
  17. print('sigma_misses = ',sigma_misses)
calc_stirling_num_recursive == sympy_stirling
sigma_hits   =  5555
sigma_misses =  3025

7.　calc_stirling_num_recursive関数にはlru_cache デコレータが適用されており、その情報をcache_info()に代入されます。

8.　当たったものはsigma_hitsにカウントします。

9.　当たっていないのはsigma_missesにカウントします。

漸化式を使った計算では、Code 3.10で作成したcalc_stirling_num_recursive関数を使うことも考えられますが、100通りの計算に対して1つ1つ関数を適用するのは相当な処理量になるので、漸化式の定義を使う方法でコンピュータへの負荷を減らすようにします。漸化式を使いスターリング数の一覧を作成し、SymPyライブラリのstirling関数と比較し正しく計算できていることを確認します。

Code 3.14　漸化式の考え方を使ったスターリング数の一覧を関数と比較

  1. accumulate_stirling_table = [
  2. [0 for _ in range(max_k + 1)]
  3. for _ in range(max_n + 1)
  4. ]
  5. accumulate_stirling_table[0][0] = 1
  6. for idx_n in range(1, max_n + 1):
  7. for idx_k in range(1, idx_n + 1):
  8. accumulate_stirling_table[idx_n][idx_k] = (
  9. accumulate_stirling_table[idx_n - 1][idx_k - 1]
  10. + idx_k * accumulate_stirling_table[idx_n - 1][idx_k]
  11. )
  12. if accumulate_stirling_table == sympy_stirling_table:
  13. print(f'accumulate_stirling_table == sympy_stirling calulate')
accumulate_stirling_table==  sympy_stirling calulate

2.　漸化式による一覧を作成するため、あらかじめ10×10の配列を用意し、全ての要素に0で初期化します。

3.　2からi=1、n=kのときスターリング数は1になるので、該当する箇所を1に変更します。

6.　1からnまでをiでカウントアップし、各々のiについて2からi-1まで（iの場合は.3.で変更済）まで、漸化式の③を使いスターリング数を計算します。

漸化式を使い、集合分割を生成する

漸化式を使い集合分割を生成します。考え方を改めて整理します。

k =1の場合

集合Nを1に分割するので、0からn-1までのnの集合を返します。

n=kの場合

集合Nをn個に分割するので、((0),(1)・・・(n-1))の集合を返します。

その他

次の2つの分割を生成します。

S(n - 1, k – 1)

新しく増えた要素は単独で1つのブロックを形成するので、S(n - 1, k – 1)で生成した集合分割の最後に(n)を追加します。

S(n - 1, k )

新しく増えた要素はS(n - 1, k )で生成した集合分割の各ブロックにn-1を追加します。このため、S(n - 1, k )の集合分割1つに対して、その集合分割のブロックの個数だけ新たに分割が作成されます。

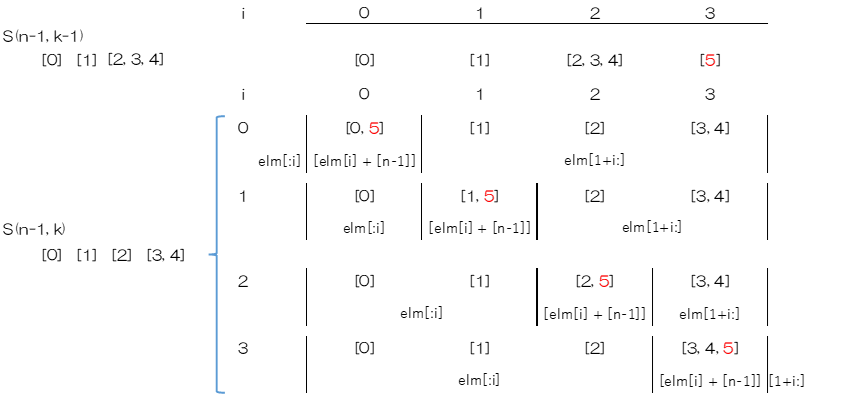
Figure 3.4　漸化式を使った多重分割の生成の考え方
漸化式を使った多重分割の生成の考え方

これらの機能を備えたgenerate_set_partition関数を作成しますが、③の2つの処理は複雑なので、補助的なinsert_parts_recursive関数を作成します。

insert_parts_recursive関数ではlevel=1とすると③-1の処理、lebel=2とすると③-2の処理をします。

Code 3.15　配列に配列やリストを挿入

  1. flat_list = [11, 12, 13]
  2. nested_list = [[11, 12], [13, 14, 15], [16, 17]]
  3. print(flat_list + [100])
  4. print(nested_list + [[100]])
  5. print(flat_list[:1] + [100,200] + flat_list[1:])
  6. print(flat_list[:1] + [*(100,200)] + flat_list[1:])
  7. print(nested_list[:1] + [[100, 200]] + nested_list[1:])
[11, 12, 13, 100]
[[11, 12], [13, 14, 15], [16, 17], [100]]
[11, 100, 200, 12, 13]
[11, 100, 200, 12, 13]
[[11, 12], [100, 200], [13, 14, 15], [16, 17]]

3.　複数の1次元リストに+演算子を適用すると、1次元リストレベルのリストが含まれるようになります。

4.　複数の2次元リストに+演算子を適用すると、第2レベルで結合されます。

5.　 1次元リストの1番目と2番目の要素の間に、複数の要素を挿入する場合ためには、スライスの機能を使います。

6.　リストの中に複数の整数をアンパックしていくと5.と同じ結果になります。

7.　2次元リストの1番目と2番目のリストの間にリストを挿入するためには、スライス機能を使い2次元リストを結合します。

Code 3.16　リストにリストや文字列を挿入する

  1. def insert_parts_recursive(data, add, level):
  2. array = []
  3. if level == 0:
  4. if isinstance(data, int):
  5. array.append((data, add))
  6. else:
  7. array.append(data + [add])
  8. else:
  9. for i in range(len(data)):
  10. for elm in insert_parts_recursive(data[i], add, level - 1):
  11. if isinstance(elm, tuple):
  12. array.append(data[:i] + [*elm] + data[i + 1:])
  13. else:
  14. array.append(data[:i] + [elm] + data[i + 1:])
  15. return array
  17. data = [[11, 12], [13, 14, 15], [16, 17]]
  18. print("Level 0:")
  19. pprint.pprint(insert_parts_recursive(data, [100], 0))
  20. print("\nLevel 1:")
  21. pprint.pprint(insert_parts_recursive(data, 100, 1))
  22. print("\nLevel 2:")
  23. pprint.pprint(insert_parts_recursive(data, 100, 2))
Level 0:
[[[11, 12], [13, 14, 15], [16, 17], [100]]]

Level 1:
[[[11, 12, 100], [13, 14, 15], [16, 17]],
 [[11, 12], [13, 14, 15, 100], [16, 17]],
 [[11, 12], [13, 14, 15], [16, 17, 100]]]

Level 2:
[[[11, 100, 12], [13, 14, 15], [16, 17]],
 [[11, 12, 100], [13, 14, 15], [16, 17]],
 [[11, 12], [13, 100, 14, 15], [16, 17]],
 [[11, 12], [13, 14, 100, 15], [16, 17]],
 [[11, 12], [13, 14, 15, 100], [16, 17]],
 [[11, 12], [13, 14, 15], [16, 100, 17]],
 [[11, 12], [13, 14, 15], [16, 17, 100]]]

5.　level0で関数を呼び出されたときには、dataの最後にaddに代入したものを追加します。

6.　dataが整数の場合は、3番目のパターンを想定しており、整数の後に整数を追加します。このとき整数を単純につなげるわけにはいかないので、7.タプルにして返します。

8.　dataが整数ではない場合は、リストの最後にaddを追加します。パターン0の場合はリスト、パターン1の場合は整数を追加しますが、いずれも同じ書き方で処理することができます。

10. level0でない場合は、引数でわたされたdataを分割して5.以下の追加の処理につなげる処理をします。

11.　dataの要素1つ1つを分割して自身の関数を再帰的に呼び出します。この際現在のレベルを1だけ小さくします。このことにより、パターン2の場合にはそれぞれのリストに対してaddを追加し、パターン3の場合にはさらに細かい整数のレベルでaddを追加することができるようになります。

13. 6から7の処理を受けて、タプルで呼び出されたときはアンパックして追加します。

さっそく、集合分割を生成します。

Code 3.17　漸化式を使い第2種スターリング数にもとづく集合分割を生成

  1. def generate_set_partition(n, k):
  2. if n == 0 and k == 0:
  3. return [[]]
  4. if n == 0 or k == 0:
  5. return []
  6. if k > n:
  7. return []
  8. partitions_list = []
  9. for elm in generate_set_partition(n - 1, k - 1):
  10. partitions_list.extend(insert_parts_recursive(elm, [n - 1], 0))
  11. for elm in generate_set_partition(n - 1, k):
  12. partitions_list.extend(insert_parts_recursive(elm, n - 1, 1))
  13. return partitions_list
  15. if (set(convert_to_tuple(sympy_partitions_list))
  16. == set(convert_to_tuple(generate_set_partition(6, 4)))):
  17. print('generate_set_partition == sympy_multiset_partitions_list')
generate_set_partition == sympy_multiset_partitions_list

2.　k=1の場合0からn-1までの要素が1つの分割になります。例えば、n=5の場合[[0, 1, 2, 3, 4]]となります。

4.　k=nの場合、0からn-1までの要素が1つずつの分割になります。例えば、n=5の場合[[0], [1], [2], [3], [4]]となります。

7.　漸化式③の左辺の処理をします。generate_set_partition (n-1, k-1)で返された多重分割について、新しいnは単独の分割になるので、これまでの分割に[[n-1]]を結合して返します。

9.　漸化式③の左辺の処理をします。generate_set_partition (n-1, k)で返された多重分割は、分割のリストがk個あります。新しいn-1はこのk個の分割のいずれかに追加して返します。

まとめ

本節では、スターリング数に関する漸化式を導出・検証し、SymPyライブラリと再帰関数、動的計画法の3種類の方法で一致することを確認しました。また、再帰関数に @lru_cache を適用することで、実行時間の大幅な短縮が可能であることも示しました。

ictsr4 All Rights Reserved.