ベル数による集合分割の生成
制約なし写像による集合の分割
ベル数について理解するため、次の問題を考えます。
Example 3.2
出席番号0から5までの6人について、4つのグループに分けタクシーを使い市内観光をします。グループは区別しないものとします。この場合に、考えられる組み合わせは何通りになりますか。なお、4台のタクシーをすべて使う必要はないものとします。
これまでは、乗らないタクシーは無いという全射の前提で考えてきました。ここでは、空車も許される制約なし写像にした場合の分割を生成し、その個数を計算します。
制約なし写像の集合分割の生成
制約なし写像の場合の具体例
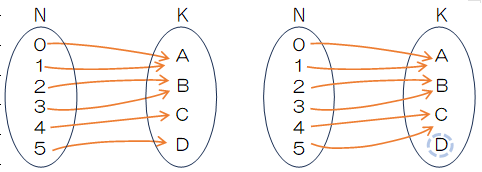
写像にすると、左側が全射の集合分割ですが、制約な写像の場合は2の(A, A, B, B, C, C)のようにDが選ばれないような分割も認められます。さらに極論ですが、 (A, A, A, A, A, A)のように、1つに集中する集合分割も考えられます。
制約なし写像の集合分割を生成するため、generate_unrestricted_perm関数を使い集合Kのラベルありの重複順列を作成し、ラベルなしにする方法で、inverse_value_map_list関数で集合Kを基準に整理し、結果をリストinverse_value_map_listに格納します。その後、増加写像の考え方を使い集合Kをラベルなしにするため、filter_increasing_map関数を適用し、set_partition_listに格納します。リストを作成したらラベルがない構造に変換し、ラベルありとラベルなしの件数の比を計算します。余りが出ないようであれば、両者の関係は単純に整理できますが、割り切れないようであれば面倒なことになりそうです。
Code 3.18 制約写像の重複順列から増加関数の考え方を使って集合Kをラベルなし構造に変換
- k_list= ['A', 'B', 'C', 'D' ]
- k = 4
- n = 6
- unrestricted_perm_list = generate_unrestricted_perm(k_list, n)
- inverse_value_map_list = inverse_value_mapping(k_list,unrestricted_perm_list)
- set_partition_list = filter_increasing_map(inverse_value_map_list)
- print(f'labeled_count : {len(unrestricted_perm_list):>7}')
- print(f'unlabeled_count : {len(set_partition_list):>7}')
- print(f'unlabeled/labeled : '
- f'{len(unrestricted_perm_list) / len(set_partition_list):>.4f}')
- inverse_value_map_list
labeled_count : 4096 unlabeled_count : 187 unlabeled/labeled : 21.9037 [((0, 1, 2, 3, 4, 5), (), (), ()), ((0, 1, 2, 3, 4), (5,), (), ()), ((0, 1, 2, 3, 4), (), (5,), ()), ((0, 1, 2, 3, 4), (), (), (5,)), ・ ((0, 1), (2, 3), (4,), (5,)), Figure 3.5の1 ・ ((0, 1), (2, 3), (4, 5), ()),Figure 3.5の2 ・ ・ ((), (), (5,), (0, 1, 2, 3, 4)), ((), (), (), (0, 1, 2, 3, 4, 5))]
19. 全射のラベル無しにすると187通りyter Notebookではリストの件数が1000を超える場合、1000行目以降は省略されるので、全てを出力するためにはpprintモジュールのpprint関数を使用します。
制約なし写像の場合、集合K(ラベルあり)の重複組み合わせは4096通りに対し、全射のラベルなしにすると187通りとなりました。比を計算すると割り切れないことから、スターリング数のように計算が単純でないことがわかります。制約なし写像の分割なので空白の要素(空のタプル())が含まれており、n(k)、つまり何台のタクシーに分乗するかが一定でないことが原因と考えられます。そこで、n(k)ごとにカウンタを使い対応する分割数を集計します。
制約なし写像とした場合の値域の個数による分類
複数の集計をする場合、リストを使う方法もありますが、カウンタにインデックスを指定して0で初期化する必要があります。その点、Pythonの標準ライブラリであるcollectionsモジュールが提供するCounterクラスを使うと初期化の手間が省けます。ラベルありのkごとの集計はlabeled_cnt、ラベルなしの集計はunlabeled_cntとします。また、n=6に対してkが1から4の場合の全射の個数も見ておきたいので、sigma_surjectiveで集計します。
Code 3.19 集合Nに対応する集合Kの個数ごとの分類
- from collections import Counter
- labeled_cnt = Counter()
- for elm in inverse_value_map_list:
- labeled_cnt[len(elm) - elm.count(())] += 1
- unlabeled_cnt = Counter()
- for elm in set_partition_list:
- unlabeled_cnt[len(elm) - elm.count(())] += 1
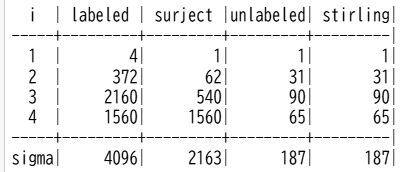
- print(f' i | labeled | surject |unlabeled|')
- print(f'-----+---------+---------+---------+')
- sigma_surjective = 0
- for i in range(1, k + 1):
- print(f'{i:^5}|'
- f'{labeled_cnt[i]:>9}|'
- f'{calc_surjective_perm(n, i):>9}|'
- f'{unlabeled_cnt[i]:>9}|')
- sigma_surjective += calc_surjective_perm(n, i)
- print(f'-----+---------+---------+---------+')
- print(f'sigma|'
- f'{sum(labeled_cnt.values()):>9}|'
- f'{sigma_surjective:>9}|'
- f'{sum(unlabeled_cnt.values()):>9}|')
2. ラベルありリストの個数を集計するため、label_cntというカウンタオブジェクトを作成します。このことにより、4.のように特に初期化をしなくてもlabel_cntのindexを集計することができます。
4. ラベルありのリストinverse_value_map_listから取り出した順列につき、要素数から空のタプルを差し引いた値、つまり集合Nと対応のある集合Kの要素数をインデックスとして、カウンタlabel_cntに加算します。
5. 同様にラベル無リストの個数を集計するunlabel_cntを作成します。
7. ラベル無しのリストset_partition_listについても4.と同じようにunlabeled_cntで集計します。
作成した表をもとに、ラベルありからラベルなしに集約する分割の過程を分析します。
ラベルありの件数
タクシー4台のうち、何台に実際に乗車するか、つまりNに対応するKの個数をxとします。x=4、つまりすべてのタクシーに乗車する場合には、PIE (6, 4)となります。次に、x=3のケースを取り上げます。ラベルありの場合2160通りあるのに対し、全射の数は540通りと差が生じ、割り返すと丁度4倍になっています。これはどこから出てくるのでしょうか。
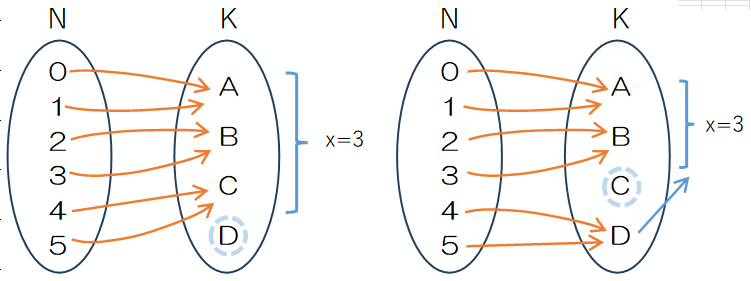
図表2の2つの写像は、集合Kの要素4つのうち3つが集合Nに対応付けられており、左はA,B,C、右はA,B,Dに分乗していることを示します。これらは、集合Kをラベル無しの分割に変換するので最終的には1つの分割に集約されますが、現段階では別の重複順列としてカウントされています。いずれも、k=4のうち3つが選ばれるので、その選び方は${}_4 C_3=4$通りあり、その各々についてPIE(6,3)通りとなります。n=6,k=3の包除原理により計算した全射の重複順列の個数との積になります。
n=6, k=4の重複分割を計算すると$ {}_4C_3\times({}_3C_1\times3^6-{}_3C_2\times2^6+{}_3C_3\times1^6)= 4\times(3^6 - 3\cdot 2^6 + 3\cdot 1^6 - 0)=4 \times 540=2160$個となります。
同様に、k=2のときには、k=4に対して一般化すると、k個からx個を選ぶ場合の重複順列は、${}_kC_x$通りに対し、集合Nを選ばれたx個に対する全射の重複順列になるので、包除原理の計算式のPIEのkをxに置き換えた数字を掛け合わせることにより個数を計算することができます。ここでは全射の重複順列の数をPIE_dist(n, k)と表現することにします。ちなみにdistはdistributionという意味で、PIEの分布という意味合いを持たせています。
Equation 3.4 制約ありでの個数ごとの順列の個数
数式を使って、制約なし写像の場合の集合Kの個数ごとの個数を計算します。関数名は制約なし写像の順列を数えるという意味でperm_unstricted_count関数とします。
ラベルがない構造に変換
(3)で求めた集合Kのラベルなしの場合の数の計算式を求めます。集合Kのラベルがないということは、k個のうちどの組み合わせを選んでも1つして数えるので式の${}_kC_x $は不要となります。また、k=3で (A,B,C)が選ばれた場合、ラベルを外すと(A,B,C)の組み合わせが増加関数の考え方から((0, 1), (2, 3), (4, 5))のみとなるので、x!=3!で割る必要があります。つまりのx=3の重複順列2160通りを$2160/ {}_4C_3 /3!= 90$通りになります。
Figure 3.7 ラベルがない構造に転換\p90130_stirling_unlabeled.png
$\sum\limits_{i=0}^{x}(-1)^i\cdot {}_xC_i \cdot(x-i)^n/x!$
この式は、結果的にはPIE_distを${}_kC_x $と$x!$で割った値、つまりスターリング数のkをxに置き換えた式になることがわかります。
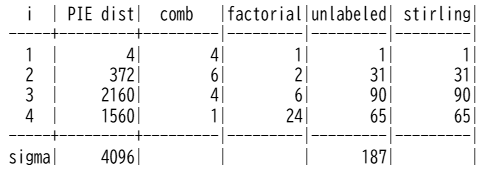
このことを確かめるためPIE_dist、${}_kC_x $、$x!$およびスターリング数を一覧にします。このプログラムでは、mathモジュールのfactorial関数とSymPyライブラリを使用するので、あらかじめインポートしておく必要があります。
Code 3.20 制約なし写像のKの数から分類を計算する関数
- def calc_PIE_dist(n, k, x):
- PIE_dist = 0
- for i in range(x + 1):
- PIE_dist += ((-1)**i) * comb(x, i) * (x - i)**n
- return int(comb(k, x) * PIE_dist)
- PIE_dist_sigma = 0
- unlabeled_sigma = 0
- print(f' i | PIE dist| comb |factorial|unlabeled| stirling|')
- print(f'-----+---------+---------|---------|---------|---------|')
- for i in range(1, k + 1):
- PIE_dist = calc_PIE_dist(n, k, i)
- PIE_dist_sigma += PIE_dist
- combination = comb(k, i, exact=True)
- factorial_k =factorial(i, exact = True)
- unlabeled = int(PIE_dist / combination / factorial_k)
- unlabeled_sigma += unlabeled
- print(f'{i:^5}|'
- f'{PIE_dist:>9}|'
- f'{combination:>9}|'
- f'{factorial_k:>9}|'
- f'{unlabeled:>9}|'
- f'{int(stirling(n, i)):>9}|')
- print(f'-----+---------+---------+---------+---------+---------+')
- print(f'sigma|'
- f'{PIE_dist_sigma:>9}|'
- f'{" ":^9}|'
- f'{" ":^9}|'
- f'{unlabeled_sigma:>9}|'
- f'{" ":^9}|')
4. $\sum\limits_{i=0}^{x}(-1)^i\cdot _{x} C _i\cdot(x-i)^n $の部分を足し込んでいきます。
14. スターリング数はSymPyライブラリのstirling関数を使って計算しました。Stirlng関数はsympy.core.numbers.Integerという形式で結果を返すのでint関数を使い整数に変換します。
PIE_distから計算した、制約なし写像、ラベルありの個数からラベルなしの個数を計算した結果とスターリング数が等しいことを確認することができました。
制約なし写像でn=kとした場合のベル数
ベル数を計算する関数
包除原理からベル数を計算する
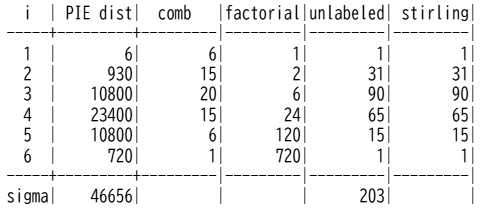
これまで、6人を4つのタクシーに分乗することを考えました。これだけでも十分贅沢ですが、数学的に考え得る最大の6台に分乗させることも考えられます。つまり集合Kをチーム数の上限をn(つまり6人を1台から1人1台まで)個まで、ラベル無し、制約無しで分割するような場合の数をベル数といい、一般にB(6)のように表します。
calc_PIE_dist関数を使ってベル数の計算をすることができますが、その際には2番目の引数kに1番目のnを、iは1からnまでをループさせその結果を足し合わせることになります。
Code 3.21 包除原理を使いベル数を計算する
- for i in range(1, k + 1):
- PIE_dist = calc_PIE_dist(n, k, i)
- PIE_dist_sigma += PIE_dist
- combination = comb(k, i, exact=True)
- factorial_k = factorial(i, exact=True)
- unlabeled = int(PIE_dist / combination / factorial_k)
- unlabeled_sigma += unlabeled
- print(f'{i:^5}|'
- f'{PIE_dist:>9}|'
- f'{combination:>9}|'
- f'{factorial_k:>9}|'
- f'{unlabeled:>9}|'
- f'{int(stirling(n, i)):>9}|')
- print(f'-----+---------+---------+---------+---------+---------+')
- print(f'sigma|'
- f'{PIE_dist_sigma:>9}|'
- f'{" ":^9}|'
- f'{" ":^9}|'
- f'{unlabeled_sigma:>9}|'
- f'{" ":^9}|')
4. calc_PIE_dist関数ではn=kなので、引数は(n, n, i)として、返り値からラベルなしの値に変換します。
ベル数を計算することができました。
Code 3.22 包除原理を使いスターリング数を経由してベル数を計算する関数
- def calc_bell_number(n):
- bell_number = 0
- for i in range(1, n + 1):
- PIE_dist = calc_PIE_dist(n, n, i)
- combination = comb(n, i, exact=True)
- factorial_i = factorial(i, exact=True)
- bell_number += int(PIE_dist / combination / factorial_i)
- return bell_number
- n = 6
- print(f'B({n}) = {calc_bell_number(n)}')
B(6) = 203
4. 包除原理を使いスターリング数を計算し、bell_number に 累積加算 していきます。最終的に、bell_number は与えられた n に対する ベル数を表します。
N=6としてベル数を計算したところ、正しい結果になりました。
SymPyライブラリを使ったベル数の計算
ベル数はSymPyライブラリのsympy.functions.combinatorial.numbersモジュールで提供される bell関数を使い計算することができます。そこでこのbell関数とcalc_bell_number関数を使いn=1から10までのベル数を計算し、結果を比較します。
Code 3.23 包除原理を使ったcalc_bell_number関数とSymPyのベル関数を比較
- from sympy.functions.combinatorial.numbers import bell
- max = 10
- print(f' n | myfunc | sympy |')
- print(f'---+---------+---------+')
- for n in range(1, max + 1):
- print(f'{n:^3}|{calc_bell_number(n):>9}|{int(bell(n)):>9}|')
6. Stirlng関数はsympy.core.numbers.Integerという形式で結果を返すのでint関数を使い整数に変換します。
calc_bell_number 関数でベル数を正しく計算できることがわかりました。ベル数による集合の分割を生成する
ベル数B(n)はS(1)からS(n)の和であることがわかりました。そこで、スターリング数による集合の分割を生成するgenerate_set_partitionを使い、ベル数による集合の分割を生成します。
Code 3.24 スターリング数による分割からベル数による分割を生成
- n = 5
- bell_list= []
- for i in range(1, n+1):
- bell_list.extend(generate_set_partition(n, i))
- len(bell_list), bell_list
(52, [[[0, 1, 2, 3, 4]], [[0, 1, 2, 3], [4]], [[0, 1, 2, 4], [3]], [[0, 1, 2], [3, 4]], [[0, 1, 3, 4], [2]], [[0, 1, 3], [2, 4]], [[0, 1, 4], [2, 3]], [[0, 1], [2, 3, 4]], [[0, 2, 3, 4], [1]], [[0, 2, 3], [1, 4]],
4. generate_set_partition関数は、複数のスターリング数の集合の分割を返すので、リストbell_listに追加するために、appendメソッドではなくextendメソッドを使います。
SymPyライブラリを使いベル数に対応する集合分割を生成する
ベル数にはSymPyライブラリのsympy.functions.combinatorial.numbersモジュールで提供される multiset_partitions関数を使い計算することができます。
Code 3.25 SymPyのmultiset_partitions関数でベル数を生成する関数
- from sympy.utilities.iterables import multiset_partitions
- n = 5
- sympy_bell_list = list(multiset_partitions(n))
- print(f'B({n}) = {len(sympy_bell_list)}')
[[[0, 1, 2, 3, 4]], [[0, 1, 2, 3], [4]], [[0, 1, 2, 4], [3]], [[0, 1, 2], [3, 4]], [[0, 1, 2], [3], [4]], [[0, 1, 3, 4], [2]], [[0, 1, 3], [2, 4]], [[0, 1, 3], [2], [4]], [[0, 1, 4], [2, 3]], [[0, 1], [2, 3, 4]], ・ ・ [[0], [1, 4], [2], [3]], [[0], [1], [2, 4], [3]], [[0], [1], [2], [3, 4]], [[0], [1], [2], [3], [4]]]
3. スターリング数の場合は分割する個数を2つ目の引数で指定しましたが、何も指定しないとベル数に対応する集合分割を返します。
4. 生成した集合分割の個数を出力します。
multiset_partitions関数によりベル数を生成し、個数もB(5)=52と正しいことが分かりました。それでは、Code 3.24で作成したスターリング数に対応して作成したベル数の集合分割とCode 3.25のSymPyライブラリのmultiset_partitions関数から生成した集合分割を比較します。
Code 3.26 自作関数とSymPyライブラリのmultiset_partitions関数を比較
- if sorted(convert_to_tuple(sympy_bell_list))==sorted(convert_to_tuple(bell_list)):
- print('bell from Stirling == SymPy multiset_partitions')
bell from Stirling == SymPy multiset_partitions
1. convert_to_tuple関数で比較をするために第1階層のみをリスト、それ以下をタプルに変換し、同じ順番に並べ替えます。
スターリング数から生成する方法が正しいことがわかりました。しかしながら、この方法は何度も同じような計算を繰り返すのであまり効率が良いとはいえません。そこで漸化式を使い、ベル数を計算し分割を生成します。
漸化式を使いベル数を計算する
ベル数の漸化式の考え方
ベル数については、ある特定の学生が何人の分割に入るかで分類すると興味深い漸化式をつくることができます。
例えば、単独で1つの分割を作る場合、残り5人で分割をつくるのでB(5)になります。次に誰か他の1人と2人で分割を構成する場合、同じ分割に入るのは5人のうち1人で5通り、その各々について他の4人でグループ分けをするのでB(4)通りとなるので5×B(4)通りになります。さらに他の2人と3人でグループを構成すると、5人のうち2人と同じグループになるので${}_5C_2$通り、その各々について残り3人でグループを作るので${}_5C_2\times B(3)$になります。以下、他の3人、4人、5人と同じグループをつくると次のとおりになります。
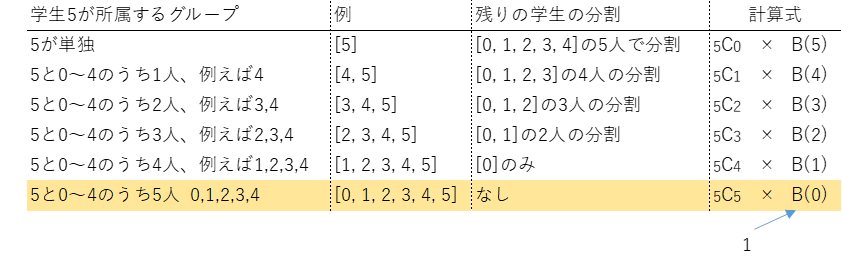
ここで、限界条件として第2種スターリング数で$S(0, 0)=1$であったことから$B(0)=1$とします。わざわざスターリング数でn=0まで計算したのはこのためです。
Equation 3.5 ベル数の漸化式
漸化式を使ってベル数を計算する
漸化式を使い0から10までのベル数を計算します。ここではリストbell_arrayでは0から変数maxまでの順次ベル数を追加します。計算結果はB(0)からB(10)までリストbell_arrayに順次追加していきます
Code 3.27 ベル数を漸化式で計算する
- max_n = 10
- bell_array = []
- for idx_n in range(0, max_n + 1):
- if idx_n == 0:
- bell_array.append(1)
- continue
- next_bell = 0
- for i in range(idx_n):
- next_bell += comb(idx_n - 1, i, exact = True) * bell_array[i]
- bell_array.append(next_bell)
- print(f' n | myfunc | sympy |')
- print(f'---+---------+---------+')
- for n, bell_number in enumerate(bell_array):
- print(f'{n:^3}|{bell_number:>9}|{int(bell(n)):>9}|')
4. 0のベル数は1なので、bell_arrayに初期値1を追加します。i=0のときはこれ以降の漸化式の計算は不要なので、continueでループを抜けてidx_n=1の処理に移行します。
8. nに格納した次のベル数をnext_bellで計算するため、漸化式に従いint(comb(n-1,k)*bell_array[k]) を次々に足し込みます。
0から10までのベル数をリストにすることができました。だいぶすっきりしてきましたが、nのベル数を計算するために、n-1以下のベル数をいちいち参照する必要があるので、もう一歩工夫が必要な気がします。
この関係を整理すると次のような再帰関数を作ることができます。The On-Line Encyclopedia of Integer Sequences (OEIS)において、A000110で情報が掲載されています(https://oeis.org/A000110)。ここでは、最大値がB(26)までの値が示されているので、計算してみます。
漸化式を使いベル数を計算する関数
Code 3.28 漸化式を使いベル数を計算する関数
- def calc_bell_number_recursive(n):
- if n == 0:
- return 1
- bell_number = 0
- for i in range(n):
- bell_number += (calc_bell_number_recursive(i)
- * comb(n - 1, i, exact=True))
- return bell_number
- print(f'B(10),{calc_bell_number_recursive(10)}')
- print(f'B(26),{calc_bell_number_recursive(26)}')
B(10)=115975 B(26)=49631246523618756274
5. B(n)を計算するために、B(0)からB(n-1)までの個数を使うので、rangeは0からn-1までをループさせればよいことになります。
少し時間はかかりますが、正しく計算することができました。想像どおりベル数は爆発的に増加することがわかります。ベル数の漸化式により、個数の計算ができることが分かったので、つぎに漸化式を使い分割を生成します。
漸化式を使ってベル数に対応する集合の分割を生成する
漸化式を使いベル数に対応する集合分割を生成する関数
ここでは、特定のNの要素(ここでは出席番号5)の学生に注目し、この学生が何人の分割に入るかで整理します。例えば3人のブロックに入るとしたら、残り4人のうち2人と同じブロックに入るので${}_4C_2$通りの組み合わせになります。この組み合わせの1つ1つに対して、ブロックに入らなかった学生2人の集合の分割を当てはめることにより生成することができます。ここで、組み合わせの選ばれる要素と選ばれない要素はgenerate_injective_comb_remaining関数を使い、与えられた集合のうち、2つを選ぶとともに、選ばれなかった5つをセットとして1つのタプルとするような、組み合わせの配列を生成します。
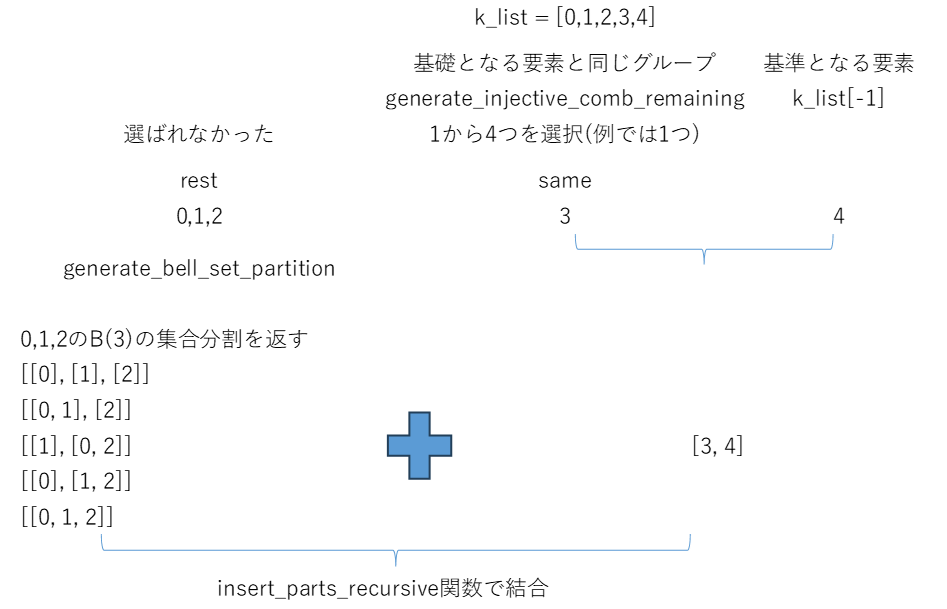
ここでいよいよ漸化式を使ったベル数に関連する集合分割を生成する関数を作成します。k_listの最後の要素(ここでは4)を基準に、generate_injective_comb_remaining関数を使い、この要素と同じ組に入る要素を0個からk-1個まで選びます、同時に最後の要素と同じ組に入らない要素を選びます。Figure 3.9では4と同じグループに入るのが1人で3とします。このとき、残り0,1,2の3人で集合分割を生成すればよいので、generate_injective_comb_remaining関数を再帰的に呼び出し、その結果の1つ1つと[3,4]とを1つの組み合わせとします。B(3)なので5通りとなる、これらと[3,4]のグループをinsert_parts_recursive関数で引数を0として実行し、その結果をリストに蓄積します。
Code 3.29 漸化式を使いベル数にもとづく集合の分割をする関数
- def generate_bell_set_partition(k_list):
- if len(k_list) == 0:
- return [[]]
- bell = []
- for i in range(len(k_list)):
- for same, rest in generate_injective_comb_remaining(k_list[:-1], i):
- for elm in generate_bell_set_partition(list(rest)):
- bell.extend(
- insert_parts_recursive(elm, list(same) + [k_list[-1]], 0)
- )
- return bell
- bell_temp = generate_bell_set_partition(range(5))
- bell_set_partition_list = convert_to_tuple(bell_temp)
- len(bell_set_partition_list), bell_set_partition_list
[((0,), (1,), (2,), (3,), (4,)), ((0,), (1,), (2,), (3, 4)), ((0,), (1,), (2, 3), (4,)), ((0,), (1,), (2, 4), (3,)), ((0,), (1,), (2, 3, 4)), ((0,), (1, 2), (3,), (4,)), ((0,), (1, 2), (3, 4)), ((0,), (1, 3), (2,), (4,)), ((0,), (1, 3), (2, 4)),
6. 選ばれる要素をsame,選ばれなかった要素をrestとして返します。restについてはここからさらに集合分割を作る必要があるので、再帰的にgenerate_bell_set_partitionを呼び出します。
7. generate_bell_set_partition関数の戻り値は、最後の要素が含まれない集合分割になるので、insert_parts_recursive関数を使い、結合してリストbellに追加します。
SymPyライブラリmultiset_partitions関数を使い、ベル数に関連する集合分割を生成
SymPyライブラリのmultiset_partitions関数により、スターリング数に関連する集合分割S(n, k)を生成することができました。これに対して、ベル数はS(n ,1)からS(n , n)までの合計なので、2番目の引数を指定しないことによりベル数に関連する分割が生成されます。ここで生成した分割と比較することによりCode 3.29が正しく機能していることを確認します。
Code 3.30 再帰関数を使とSymPyライブラリで生成した集合分割を比較
- if sorted(
- [tuple(sorted(part)) for part in convert_to_tuple(bell_set_partition_list)]
- ) == sorted(
- [tuple(sorted(part)) for part in convert_to_tuple(sympy_bell_list)]
- ):
- print('bell by recursive == SymPy SetPartitions')
bell by recursive == SymPy SetPartitions
3. multiset_partitions関数の出力結果はジェネレータ形式形式 なので、個数を数えたり他のリストと比較するため、list関数を使いリストに変換します。
結果、正しいことがわかりました。