第1種スターリング数と循環分解

スターリング数に円順列を適用した第1種スターリング数

例題で見る第1種スターリング数

これまでスターリング数ついてみてきましたが、実はこれは第2種スターリング数と呼ばれるもので、ここではもう1つのスターリング数、第1種スターリング数についてご紹介します。

Example 3.3

出席番号0から5までの6人の学生が、それぞれ1つずつプレゼントを持ち寄り、よくかきまぜて交換し合うというゲームを考えます。例えば、1が持参したプレゼントを3が、3のものを4が、４のものを1が受け取る場合1→3→4→1と表すと、0→5→0、2→2（自分のプレゼントが自分に当たることもある）のように表すことができ、これで1通の組み合わせとして数えます。

（１）考えられる組み合わせは何通りになりますか。

（２）例にある合わせでは6人を3つのグループに分かれることになります。同じく（１）のうち、3つのグループに分かれるような組み合わせは何通りありますか。

（１）については、0のプレゼントを受け取ることができるのは1～5の5人、その各々のケースにつき1のプレゼントを受け取ることができるのは残りの4人、と順次考えていくと単純な順列の問題になります。このため人数が6人なので、答えは${}_6P_6=6!=720通り$6の階乗で720通りになります。これを写像で表すと図の通りになります。ただし例題のように表すとかなり複雑になるのでループスのようにして表した方がイメージを掴みやすいと思います。

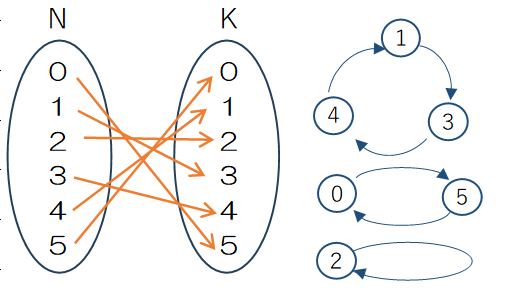
Figure 3.1　漸化式を使った多重分割の生成の考え方
漸化式を使った多重分割の生成の考え方

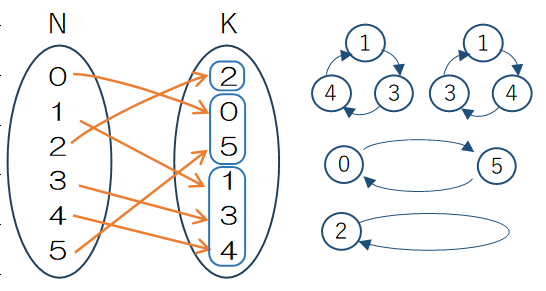
（２）については、持ち寄ったプレゼントを交換するためにグループごとにテーブルを用意すると、テーブルが何台必要かという問題になります。ラベルのある6人をラベルのない3つグループに分けているので、これまでのスターリング数S(6,3)となりそうに思えます。ところが、これまでのスターリング数では1,3,4のグループは1つとして数えますが、1→3→4→1、1→4→3→1では3人が受け取るプレゼントは異なるので、別のものとして数える必要があります。このように、集合への分割に加えてプレゼントが渡る循環を考慮する必要があります。このような場合の数を第1種スターリング数といい、n個の要素をk個の循環に分ける方法を循環分解（cycle decomposition）といいます。また、循環分解の中のグループを循環(cycle)といい、循環分解の中の循環の数をサイクル数といいます。それでは次章以下では第1種スターリング数の計算と循環分解の生成について検討します。

Figure 3.2　漸化式を使った循環分解の生成の考え方
漸化式を使った循環分解の生成の考え方

円順列とは

円順列の考え方

第2種スターリング数に基づく集合分割の各分割において円順列の処理を施すことにより、第1種スターリング数に基づく循環分解を求めることができます。つまり分割内での分解（プレゼントのわたり方）を表す順列を円順列（circular permutation）といいます。それでは、まず円順列を生成するところからはじめます。

円順列は回転して同じ並び方になるものは同じ配置とみなす順列をいいます。例えば、順列において、図表のようにパーティーの円卓での並び順のイメージで、４つの順列は円順列では1通りとして数えます。

したがって、要素数nの円順列の個数を$C(n)$とすると$C(n)= (n−1)!$で計算することができます。

また要素数5の円順列は、4の円順列に対し新しく要素が割り込む場所は図の通り4か所あるので円順列の個数は4倍になります。このように、円順列には次のような漸化式$C(n)=(n−1)⋅C(n−1),n≥2$の関係にあることがわかります。

円順列を生成するためには次のように１つの要素、例えば０を固定しておいて残りの要素で順列を考えるとわかりやすくなります。固定代表元法（fixing representative）

集合の分割の1つ1つにつき円順列をしたものをいいます。

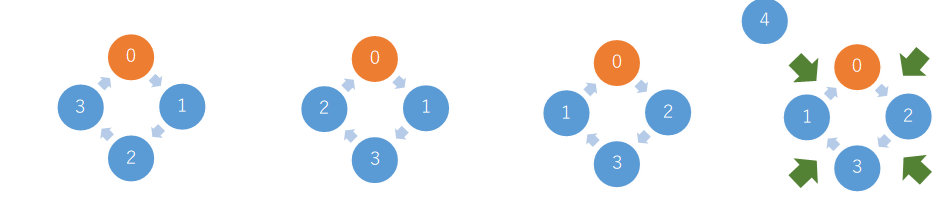
Figure 3.4　円順列で要素を1つ増やす
円順列で要素を1つ増やす

n個を要素とする集合の円順列、およびn個の要素の集合に要素を1つ追加したときの円順列は次の通り計算します。n=4の円順列に対して、5人目が現れた時には、従来の4人のうちいずれかの右側（または左側）に割り込むことによりn=5の円順列を生成することができます。このことから円順列の個数は次の数式で計算することができます。

Equation 3.6　円順列の計算

$C(n)=(n-1)!$
$C(n)=nC(n-1)$

円順列を生成する関数

Pythonのitertoolsモジュールには円順列を生成する関数がないので、以前作成した順列を生成する関数を使って作成します。

Code 3.32　順列から円順列を生成

  1. def generate_circular_perm(k_list):
  2. first = k_list[0]
  3. rest = generate_injective_perm(k_list[1:], len(k_list) - 1)
  4. circular_list = []
  5. for elm in rest:
  6. circular_list.append((first,) + elm)
  7. return circular_list
  9. k_list = [0, 1, 2, 3]
  10. circular_perm_list = generate_circular_perm(k_list)
  11. print('circular_permutations_count =', len(circular_perm_list))
  12. circular_perm_list
circular_permutations_count= 6
[(0, 1, 2, 3),
 (0, 1, 3, 2),
 (0, 2, 1, 3),
 (0, 2, 3, 1),
 (0, 3, 1, 2),
 (0, 3, 2, 1)]

4.　k_listのうち0番目の要素を固定するものとして、firstという変数に割り当てます。

5.　k_listの1番目以降に対して順列を生成するperm_injective_funcを実行し、戻り値をrestに代入します。このため、作成する順列の数はn-1になります。

集合分割において要素数6の集合を3つに分割していますが、3つの分割に対してそれぞれ円順列を生成します。

① 2だけを要素とする集合で円順列は0!=1個になります。

② 0と5の2つを要素とする集合で、円順列は1!=1個になります。

③ 1,2,3の3つを要素とする集合で、円順列は(3-1)!=2個になります。

したがって図のような分割に対して循環分解の個数は③により、2倍になることがわかります。

第1種スターリング数は、第2種スターリング数に関わる集合の各々の分割に対し、円順列を生成したときの組み合わせの個数をいいます。また、この際の分割を循環分割（cycle partition）といいます。これを表したのが図です。ここでは6つの要素を3つに分割するので小文字のsを使い、s(6, 3)と表します。第2種スターリング数は大文字のSを使うので、後者の方が偉いというような逆転現象が起きています。

集合分割に円順列の処理をして循環分解に変換

第1種スターリング数に対応する循環分解は、第2種スターリング数に対応する集合分割を基に、各ブロックに対して円順列を掛け合わせたものとみなせます。この考え方をもとに集合分割を生成します。

generate_set_partition関数を使い集合分割を生成し、各集合分割のブロックから円順列を生成し、リストcircular_permに追加していきます。

Code 3.33　第2種スターリング数から第1種スターリング数を生成

  1. n = 6
  2. k = 4
  3. cyclic_set_partition_list = []
  4. for partition in generate_set_partition(n, k):
  5. circular_perm = [()]
  6. for block in partition:
  7. temp = circular_perm
  8. circular_perm = []
  9. for elm in temp:
  10. for circular_item in generate_circular_perm(block):
  11. circular_perm.append(elm + (tuple(circular_item),))
  12. cyclic_set_partition_list.extend(circular_perm)
  14. print(f's({n}, {k}) = {len(cyclic_set_partition_list)}')
  15. cyclic_set_partition_list
s(6, 4) = 85
[((0, 1, 2), (3,), (4,), (5,)),
 ((0, 2, 1), (3,), (4,), (5,)),
 ((0, 1, 3), (2,), (4,), (5,)),
((0,), (1, 4), (2,), (3, 5)),
 ((0, 5), (1,), (2, 4), (3,)),
 ((0,), (1, 5), (2, 4), (3,)),
 ((0,), (1,), (2, 4, 5), (3,)),
 ((0,), (1,), (2, 5, 4), (3,)),
 ((0,), (1,), (2, 4), (3, 5)),
 ((0, 5), (1,), (2,), (3, 4)),
 ((0,), (1, 5), (2,), (3, 4)),
 ((0,), (1,), (2, 5), (3, 4)),
 ((0,), (1,), (2,), (3, 4, 5)),
 ((0,), (1,), (2,), (3, 5, 4))]

11.　これまで生成した循環分解に新たに生成した円順列のブロックを追加します。elmはこれまで生成したブロックで2次元のタプルであるのに対して、circular_itemは1次元のタプルなので、結合するためには、(circular_item,)とすると2次元のタプルに変換することができます。

12.　 circular_permは1つの集合分割に対して円順列の処理をして増やした3次元の配列になので、これまで生成したcirculer_permに追加しているのでextendメソッドを使用します。

s(6, 4) = 85となりました。このプログラムが正しいかは、SymPyなどの関数を使い検証していきます。

第1種スターリング数に関わる既存のライブラリの関数

SymPyライブラリによる第1種スターリング数に関する関数

これまで第2種スターリング数はSymPyライブラリのsympy.functions.combinatorial.numbersモジュールで提供されるstirling関数を使い計算してきましたが、実は第1種スターリング数も同じ関数により計算することができます。この関数にはkindというパラメータがあり、kind=1とすると第1種スターリング数を計算するようになります。つまり、デフォルトはkind=2で2種スターリング数を計算することになり、ここでも逆転現象が見られます。

Code 3.34　SymPyライブラリのstirling関数で第1種スターリング数を計算

  1. from sympy.functions.combinatorial.numbers import stirling　
  2. print(f's({n}, {k}) = {stirling(n, k, kind=1)}')
s(6, 4) = 85

2.　 パラメータにkind=1を追加することにより、第1種スターリング数を計算します。

Code 3.33の結果と一致していることがわかります。

SageMathのto_cyclesメソッドにより順列を循環分解に変換

SageMathのto_cyclesメソッドで順列を循環分解に変換

循環分解を直接生成する関数は、Pythonの既存のライブラリには見当たりません。SageMathにも直接は生成する機能はありませんがには、順列から循環に分解するto_cyclesメソッドがあります。そこで、SagaMathでPermutations関数を使い、リストpartitionに整数1から6までの順列を生成し、その1つ1つに対してto_cyclesメソッドを適用し、巡回表現に変換します。順列を1から6としたのは、to_cycleメソッドが1-baseでないとエラーになるためです。ここでは、今回はs(6, 4)を求めるのでサイクル数4のものだけを抜き出し、リストcyclic_partition_6_4に格納します。

Code 3.35　SageMathによる順列から循環分解の生成

  1. partition = Permutations(range(1, 7))
  2. cyclic_partition=[]
  3. for elm in partition:
  4. cyclic_partition.append(elm.to_cycles())
  5. cyclic_partition_6_4 = []
  6. for partition in cyclic_partition:
  7. if len(partition) == 4:
  8. cyclic_partition_6_4.append(partition)
  9. cyclic_partition_6_4
sage_cyclic_set_partition = [
 ((1,), (2,), (3,), (4, 5, 6)),
 ((1,), (2,), (3,), (4, 6, 5)),
 ((1,), (2,), (3, 4), (5, 6)),
 ((1,), (2,), (3, 4, 5), (6,)),
 ((1,), (2,), (3, 4, 6), (5,)),
 ((1,), (2,), (3, 5, 4), (6,)),
 ((1,), (2,), (3, 5, 6), (4,)),
 ((1,), (2,), (3, 5), (4, 6)),
 ((1,), (2,), (3, 6, 4), (5,)),
 ((1,), (2,), (3, 6, 5), (4,)),
 ((1,), (2,), (3, 6), (4, 5)),
 ((1,), (2, 3), (4,), (5, 6)),

1　Permutations関数で順列を生成することができます。ここでの出力はsage.combinat.permutation.StandardPermutations_n_with_category.element_class'という特殊な形式です。

4.　to_cyclesはメソッドになるので、順列を格納したリストelmの後に配置します。

len(partition)はpatritonの中のタプル、つまりサイクル数を表すので4のものがs(6 ,4)になります。

SageMathのリストをPythonにコピー

SageMathで生成した循環分解のリストをPythonで使うためにコピーします。ここでは、最も手早い方法として、単純にコピペしてリストとしての形にします。

Code 3.36　 sagemath cellからs(6, 4)の循環分解をコピー

sage_cyclic_set_partition = [
 ((1,), (2,), (3,), (4, 5, 6)),
 ((1,), (2,), (3,), (4, 6, 5)),
 ((1,), (2,), (3, 4), (5, 6)),
 ((1,), (2,), (3, 4, 5), (6,)),
 ((1,), (2,), (3, 4, 6), (5,)),
 
 ((1, 6, 4), (2,), (3,), (5,)),
 ((1, 6, 5), (2,), (3,), (4,)),
 ((1, 6), (2,), (3,), (4, 5)),
 ((1, 6), (2,), (3, 4), (5,)),
 ((1, 6), (2,), (3, 5), (4,)),
 ((1, 6), (2, 3), (4,), (5,)),
 ((1, 6), (2, 4), (3,), (5,)),
 ((1, 6), (2, 5), (3,), (4,)),
]

1.　 sage_cyclic_set_partition = [という形でリストを定義します。

循環分解の計算結果をSageMathの計算結果と確認

要素を変換する関数の作成

2.1で循環分割から変換した循環分解とSageMathで生成した循環分割を比較します。こ個で問題になるにはSageMathでの結果は1-baseとなっているので直接比較することができません。ここでは、SageMathが正解であると想定して、後者から歩み寄って0-baseから1-baseに変換して比較します。このような変換は今後も必要になることを想定して、関数を作成します。引数として、変換の対象のリストをstructure、変換前の値をfrom_values、変換後の値をto_valuesとしてタプルまたはリストの形式で渡します。from_valuesはオプションとし、指定しない場合はto_valuesの個数に応じてrangeオブジェクトで指定します。また、structureにfrom_valuesにない要素がある場合は、ワーニングを出力します。

convert_index関数はシーケンスsequenceの各要素の値を、souece、targetのシーケンスで定めるルールに従って置き換えます。例えばtest_data = [(1, 2), ([3, 4], (3, 2, 0))]に対して、source = [0, 1, 2, 3, 4, 5]の値からtarget = [0, 2, 4, 6, 8, 10]に変換します。また、sourceを省略した場合は、0からtargetの個数-1までの連番をrange関数を使って指定します。なお、シーケンスは、タプルとリストを想定し、元のデータ構造の型を保ったまま結果を返します。この際、シーケンスの階層が深い場合にも対応できるよう、再帰関数を使い深さに応じ再帰します。

Code 3.37　リスト、タプルの値を対応表により使い変換

  1. def convert_index(sequence, target, source=None):
  2. if source is None:
  3. source = range(len(target))
  4. conversion_dict = dict(zip(source, target))
  5. if isinstance(sequence, tuple):
  6. return tuple(convert_index(item, target, source) for item in sequence)
  7. elif isinstance(sequence, list):
  8. return [convert_index(item, target, source) for item in sequence]
  9. else:
  10. try:
  11. return conversion_dict[sequence]
  12. except KeyError:
  13. print(f'{sequence} not in source')
  14. return float('nan')
  16. test_data = [(1, 2), ([3, 4], (3, 2, 0))]
  17. source1 = [0, 1, 2, 3, 4, 5]
  18. target1 = [0, 2, 4, 6, 8, 10]
  19. print(convert_index(test_data, target1, source1))
  20. source2 = [1, 2, 3, 4, 5]
  21. target2 = [0, 2, 4, 6, 8]
  22. print(convert_index(test_data, target2, source2))
  23. target3 = range(1, 7)
  24. print(convert_index(test_data, target3))
[(2, 4), ([6, 8], (6, 4, 0))]
0 not in source
[(0, 2), ([4, 6], (4, 2, nan))]
[(2, 3), ([4, 5], (4, 3, 1))]

4.　効率的に変換するため、sourecの要素をキーにtargetの要素とともに辞書形式に変換します。

5.　isinstance関数を使いsequenceの型をチェックし、タプルであれば、さらに自身を再帰的に呼び出し、最終的な戻り値をタプルとして返します。

7.　sequenceがリストの場合は、再帰の結果、最終的な戻り値をリストとして返します。

9.　sequenceが上記以外の場合はstructureは整数（int型）などの具体的な値になっていると考えられるのでconversion_dictを使って要素を変換します。

12.　sourceの中にsequenceにない値がある場合、nanと変換し、警告を出力します。

第2種スターリング数経由とsagemathに循環分解を比較

Code 3.38　第2種スターリング数経由とsagemathに循環分解を比較

  1. cyclic = convert_index_table(cyclic_set_partition_list, range(1,7))
  2. if sorted(cyclic)==sorted(sage_cyclic_set_partition):
  3. print('stirling_1 from 2 == sage_to_cycles')
stirling_1 from 2  == sage_tocycle

1.　 convert_index_table関数を使い、第2種スターリング数経由のリストを1-baseに変換します。

両者が一致することから、第2種スターリング数の各ブロックを円順列に変換することにより循環分解に変換できることが分かりました。

第1種スターリング数に関わる漸化式の作成

第1種スターリング数に関わる一覧の作成

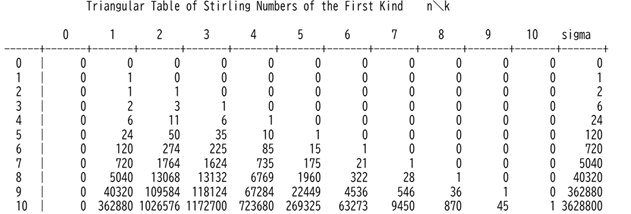
次にと同じように第1種スターリング数の一覧を作成します。print_table関数を使用するのであらかじめ実行しておく必要があります。また、桁数を１つ増やします。

Code 3.39　 SymPyライブラリのstirling関数による第1種スターリング数覧の作成

  1. max_n = 10
  2. max_k = 10
  3. stirling_1_sympy = [
  4. [0 for _ in range(max_k + 1)]
  5. for _ in range(max_n + 1)
  6. ]
  7. for idx_n in range(max_n + 1):
  8. for idx_k in range(max_k + 1):
  9. stirling_1_sympy[idx_n][idx_k] = int(stirling(idx_n, idx_k, kind=1))
  10. title = 'Triangular Table of Stirling Numbers of the First Kind n＼k'
  11. print(title.center(90))
  12. print()
  13. print_table(stirling_1_sympy, 5)
     第1種スターリング数の一覧表

4.　縦10、横11の2次元のリストの表を作成し、全ての要素に0を代入します。

23. stirling関数でkind=1を指定します。

24. 桁数が多くなるのでwを1つ増やします。

第1種スターリング数の漸化式

スターリング数の一覧表から漸化式を導く

第1種スターリング数についても、第2種スターリング数と同じように漸化式を使い計算します。

①　k=1の場合

学生がn人いてテーブルが1台の場合、円順列はn-1!になります。第2種スターリング数での1と異なる点です。

②　n=kの場合

n人が1人1台のテーブルに座る場合、第2種スターリング数と同じく1になります。

③　①②以外の多くの場合

前例のようにs(6, 4)、つまり、6人が4台のテーブルに座っていました。ところが学生が１人増えることになり、テーブルを1台増やすことを想定し、s(7, 5)と比較します。

s(6, 4)とs(7, 5)の差は、新しく来た学生の扱いにより、次の2つのケースが考えられます。

１　新しく来た学生は1人でテーブルに座る。この場合、他の6人はそのままなので、新しい分割の数はs(6, 4)と等しくなります。

２　学生が増えるのを前提に予め6人を5台のテーブルに座らせておき、つまりs(6,5)の状態から、新しい学生は円順列の追加の考え方で、6人のうちいずれか1人の隣に座るのでその6倍になります。

1,2は背反で同時に起こることはありえないので、s(7,5)=s(6,4)+s(6,5)×6=85+15×6=175となります。第2種スターリング数と比較する形で漸化式を示しておきます。

Equation 3.7　スターリング数の漸化式

境界条件１

① $s(n,1) = 1 \quad (n \geq 1)$

② $s(n,n) = 1 \quad (n \geq 0)$

境界条件２

$s0,0) = 1 \quad$
$s(n,0) = 0 \quad (n \geq 1)$
$s(0,k) = 0 \quad (k \geq 1)$

再帰関係

③$s(n, k) =S(n-1, k-1)+k\; s(n-1, k)$

ここでも、境界条件をn,kが0のときにも拡張すると境界条件２になります。ここで、第２種スターリング数と比べると、境界条件２を使うと両者を共通化することができ、なおかつ再帰関係も、2項目（引数：n-1, k）の乗数がkかn-1の違いだけになります。

以前に発展的な展開で境界条件２の方が適切との理由の1つはここにあります。

漸化式の確認

漸化式の再帰関係について確認します。

Code 3.40　 SYmPyライブラリのstirling関数により漸化式を確認

  1. print(f'S({n - 1}, {k - 1}) = {stirling(n - 1, k - 1, kind=1)}')
  2. print(f'S({n - 1}, {k}) = {stirling(n - 1, k, kind=1)}')
  3. print(f'S({n}, {k}) = {stirling(n, k, kind=1)}')
  4. result = (
  5. stirling(n - 1, k - 1, kind=1)
  6. + (n - 1) * stirling(n - 1, k, kind=1)
  7. )
  8. print(f'S({n - 1}, {k - 1}) + {n - 1} × S({n - 1}, {k}) = {result}')
S(5, 3) = 35
S(5, 4) = 10
S(6, 4) = 85
S(5, 3) + 5 × S(5, 4) = 85

4.　式が長くなるので行に分割してresultに結果を代入します。

第2種スターリング数の計算する漸化式はすでに作成していますが、stirling関数に倣いここに第1種スターリング数を計算する機能を追加します。このとき、k=1のときは$(n-1)!$となりますが、階乗を使うのは面倒なので②と③があるので0ならば0を返すようにすることで足ります。

漸化式を使いスターリング数を計算

第1種および第2種スターリング数を計算する関数

Code 3.41　漸化式を使いスターリング数を計算

  1. from functools import lru_cache
  2. @lru_cache
  3. def calc_stirling_num_recursive(n, k, kind=2):
  4. if k == 0 and n == 0:
  5. return 1
  6. if k == 0 or n == 0:
  7. return 0
  8. multiplier = k if kind ==2 else n - 1
  9. return (
  10. calc_stirling_num_recursive(n-1, k-1, kind) +
  11. multiplier * calc_stirling_num_recursive(n-1, k, kind)
  12. )
  14. calc_stirling_num_recursive(6, 4, 1),calc_stirling_num_recursive(6, 4,)
85

4.　K=1にすると第1種と第2種では計算が異なりますが、k=0にすると分けなくてすみます。

SymPyのstirling関数と漸化式による関数を比較

さっそく、stirling_recursive関数が正しく計算できることを確認します。

次に、漸化式の考え方を使い、第1種スターリング数の一覧表を作成し、Code 3.39で作成したものと比較します。

図のとおり、S(n-1, k-1)においては、新しく増えた5は単独の新しい多重分割になるので、リストとして追加します。

Code 3.42　 SymPyのstirling関数と漸化式による関数を比較

  1. accumulate_stirling_table = [
  2. [0 for _ in range(max_k + 1)]
  3. for _ in range(max_n + 1)
  4. ]
  5. accumulate_stirling_table[0][0] = 1
  6. for idx_n in range(1, max_n + 1):
  7. for idx_k in range(1, idx_n + 1):
  8. accumulate_stirling_table[idx_n][idx_k] = (
  9. accumulate_stirling_table[idx_n - 1][idx_k - 1]
  10. + (idx_n - 1) * accumulate_stirling_table[idx_n - 1][idx_k]
  11. )
  13. if accumulate_stirling_table == stirling_1_sympy:
  14. print('table from recursive == table by Sympy')
table from recursive == table by Sympy

3.　 縦10、横11の2次元のリストの表を作成し、全ての要素に0を代入します。

漸化式から循環分解を生成する

循環分解を生成する関数

s(n-1, k-1)に対しては、新しく増えた5はすでに4つある多重分割のいずれかに追加されるので、4つの重複分割に順次追加していきます。この考え方により、多重分割を生成するcyclic_partitions_func関数を作成します。第2種スターリング数から生成した分割を通すのは面倒なので、再帰関数を使い直接に生成し、#と比較します。

Code 3.43　漸化式の考え方を使い集合の循環分解を生成

  1. def generate_cyclic_set_partition(n, k):
  2. if n == 0 and k == 0:
  3. return [[]]
  4. if n == 0 or k == 0:
  5. return []
  6. if k > n:
  7. return []
  8. partitions_list = []
  9. for elm in generate_cyclic_set_partition(n - 1, k - 1):
  10. partitions_list.extend(insert_parts_recursive(elm, [n - 1], 0))
  11. for elm in generate_cyclic_set_partition(n - 1, k):
  12. partitions_list.extend(insert_parts_recursive(elm, n - 1, 2))
  13. return partitions_list
  15. n = 6
  16. k = 4
  17. cyclic_list_from_recursive = generate_cyclic_set_partition(n, k)
  18. print(f'S({n}, {k})={len(cyclic_list_from_recursive)}')
  19. cyclic_list_from_recursive
S(6, 4)=85
[[[0, 1, 2], [3], [4], [5]],
 [[0, 2, 1], [3], [4], [5]],
 [[0, 3, 1], [2], [4], [5]],
 [[0, 1, 3], [2], [4], [5]],
 [[0, 1], [2, 3], [4], [5]],
 
 [[0], [1], [2], [3, 4, 5]]]

2.　k = 1 の場合、0 から n−1 までの全要素を 1つの循環にまとめます。したがって

n = 5 のときは [[0, 1, 2, 3, 4]] となります。

4.　k = n の場合、0 から n−1 までの各要素が、それぞれ 1 要素ずつの独立した循環になります。例えば、n = 5 のときは [[0], [1], [2], [3], [4]] となります。

7.　漸化式の第 1 項（S(n−1, k−1)）に対応する処理です。`multiset_func(n−1, k−1)` が返す分割に対し、新しい要素 n−1 を 1 要素のグループ [[n−1]] として追加し、既存の分割に結合します。

9.　漸化式の第 2 項（k × S(n−1, k)）に対応する処理です。`multiset_func(n−1, k)` が返す k 個のグループから成る分割に対し、新しい要素 n−1 を各グループの任意の位置に挿入した新たな分割を生成します。

これを、0から５までの順番に並べ替えたものが２です。１の集合は第１種スターリング数のs(1)からs(6)に対応する循環分解になります。一方２の集合は、0から5までの順列になります。集合１から集合２は順番を並べ替えただけなので写像となります。一方、２から１についても、プレゼントの流れを追っていくと、循環のグループ分けをすることができ、なおかつ循環を表すことができます。したがって全単射となります。このとは第1種スターリング数の合計は階乗と等しくなります。第2種に対してベル数を計算するのは大変でしたが、複雑な処理を加えて第1種のほうが簡単に合計を計算することができるのは不思議なことです。

漸化式を使って生成した循環分解とSageMathの結果と比較

s(6, 4)についてSageMathで生成したものと、漸化式を使った関数で生成したものを比較して正しく計算できていることw確認します。この際にも、SageMathが正解と考えconvert_index_table関数で0-baseから1-baseに変換します。

Code 3.44　漸化式による方法とsageの循循環分解を比較 44

  1. converted_list = convert_index_table(cyclic_list_from_recursive, range(1,8))
  2. cyclic_from_recursive = convert_to_tuple(converted_list)
  3. if sorted(cyclic_from_recursive)==sorted(sage_cyclic_set_partition):
  4. print('sorted cyclic_from_recursive==sorted sage_cyclic_set_partition')
sorted cyclic_from_recursive==sorted sage_cyclic_set_partition

4.　 生成する順番が異なることも想定して、sorted関数を使い並べ替えてから比較します。　

漸化式によって　とSagaMathによる循環分解が、並べ替えをすることにより等しいことが分かりました。このことからも、SageMathの順列から循環分割を生成するto_cyclesメソッドをPythonにも欲しくなります。そこで、ここでは順列を表すリストから巡回表現を生成する関数を作成します。

順列から循環分解へ変換する関数を作成

順列から循環分解へ変換する関数

１つの順列であるpermを引数として、循環分解に変換するto_cyvles関数を作成します。循環分解はcyclesに蓄積することとして、複数のサイクルを扱うので2階層のリストとします。リスト[5, 3, 2, 4, 1, 0]から[(0, 5), (1, 3, 4), (2, 2)]に変換る例をとると次のようになります。

リストの0番目から処理を始めるので、cycleに0を追加し、0は5に移るのでcycleに同じ循環として5を追加します。次にインデックス5は0に移りここでこの循環は完結します。次に、リストのインデックス1を見ますが、このときに1がすでに循環に含まれていないことを確認する必要があります。このコントロールをするのがリストseenです。seenははじめはFalseで初期化しますが、cycleに追加する時点で該当するインデックスをTrueに置き換えます。このため、新規にcycleを作成する際にseenを検索し、まだ使われていないことを示すFalseであることを条件とします。

Code 3.45 　T順列を循環分解するTo_cycles関数をPythonで作成

  1. def to_cycles(perm):
  2. n = len(perm)
  3. seen = [False] * n
  4. decomposition = []
  5. for i in range(n):
  6. if not seen[i]:
  7. cycle = []
  8. j = i
  9. while not seen[j]:
  10. seen[j] = True
  11. cycle.append(j)
  12. j = perm[j]
  13. decomposition.append(tuple(cycle))
  14. return decomposition
  16. partition1 = (5, 3, 2, 4, 1, 0)
  17. print(f'cycle of {partition1} = {to_cycles(partition1)}')
  18. partition2 = (5, 4, 2, 1, 3, 0)
  19. print(f'cycle of {partition2} = {to_cycles(partition2)}')
cycle of (5, 3, 2, 4, 1, 0) = [(0, 5), (1, 3, 4), (2,)]
cycle of (5, 4, 2, 1, 3, 0) = [(0, 5), (1, 4, 3), (2,)]

3.　permと同じ要素数のリストを、まだ処理が終わっていないという意味を込めてFalseで初期化します。

7.　はじめはインデックス0、インデックス0を含む循環の処理が終わったら、新しい循環cycleを作成します。この際、そのインデックスがseenでFalseになっていることを条件とします。

この際、第1種スターリング数と比較するため、巡回表現のサイクル数ごとにリストに整理してcycle_from_injectiveに格納します。generate_injective_perm関数で生成したn=6の順列の1つ1つをpermとし、to_cycles関数でcycleに変換します。

出力結果cycle_from_injectiveは4階層のリストで、第3階層cycle1つの循環表現となり第4階層がその中のブロックになります。ここではcycleの要素数、つまりブロック数を添え字としてcycle_from_injectiveに追加するので、第2階層は0から6のk、つまりブロック数ごとの循環分割が格納されることになります。

順列を循環表現に変換

順列から循環分割を生成

まとめとして、順列からto_cycles関数でしたものと、漸化式から生成したものについてn=6に対して、k=1から6までを生成して個数と循環分解を比較し、両者が正しく作成できたことが推測することができます。

n=6の全ての順列を循環分解に変換したものをサイクル数により整理し、サイクル数ごとに漸化式から生成した結果と比べ、循環分解の個数と内容を比較します。

Code 3.46　n=6の順列をto_を循環分解に変換し、cycles関数で循環分割に変換

  1. cycle_from_injective =[[] for _ in range(n+1)]
  2. for perm in generate_injective_perm(range(n), n):
  3. cycle = to_cycles(perm)
  4. cycle_from_injective[len(cycle)].append(cycle)
  5. cycle_from_injective
[[],
 [[(0, 1, 2, 3, 4, 5)],
  [(0, 1, 2, 3, 5, 4)],
  [(0, 1, 2, 4, 5, 3)],
  [(0, 1, 2, 4, 3, 5)],
  [(0, 1, 2, 5, 4, 3)],
  [(0, 1, 2, 5, 3, 4)],
  
  [(0, 4, 1, 2, 5, 3)],
  [(0, 4, 3, 1, 2, 5)],

2.　kごとに0からnまでの循環分解を格納するための2階層のリストを初期化します。

4.　generate_injective_permで関数を順列を生成し、それぞれをpermとして取り出しto_cycles関数を適用します。

本来であれば、関数にリストで渡し、そのリストに基づいて循環分割を返すようにしたいところですが、処理が複雑になるので0からn-1までのrangeで渡すようにしています。そこで、返り値からリストを介して

リストやタプルも1次元であれば簡単に変換できますが、2次元以上になると難しいものがあります。

漸化式から生成した関数と比較する

漸化式を用いたgenerate_cyclic_set_partition関数を使い生成した循環分割と、順列から

to_cycle関数を使い巡回表現に変換したリストが一致していることを確認します。n=6として、k=1からk=6まで順次比較し、最後に合計が$n!=6!$になっていることを確認します。

Code 3.47　n=6のときkごとの件数の比較

  1. n = 6
  2. sigma = 0
  3. for k in range(1, n+1):
  4. cyclic_list_from_recursive = generate_cyclic_set_partition(n, k)
  5. if (
  6. sorted(convert_to_tuple(cycle_from_injective[k]))
  7. == sorted(convert_to_tuple(cyclic_list_from_recursive))
  8. ):
  9. stirling_num = len(cycle_from_injective[k])
  10. sigma += stirling_num
  11. print(f's({n},{k}) = {stirling_num:>4} -> from_perm = recursive ')
  12. print(f'sum of stirling({n},k)={sigma}')
  13. print(f'factorial of {n} ={factorial(n)}')
s(6,1) =  120 -> from_perm = recursive 
s(6,2) =  274 -> from_perm = recursive 
s(6,3) =  225 -> from_perm = recursive 
s(6,4) =   85 -> from_perm = recursive 
s(6,5) =   15 -> from_perm = recursive 
s(6,6) =    1 -> from_perm = recursive 
sum of stirling(6,k)=720
factorial of 6      =720.0

4.　kごとに等しい時にはその旨と件数を表示します。

SageMathでは順列にto_cyclesをメソッドに適用しましたが、ここではto_cycles関数としましたが、同じ機能を適用することができました。

ictsr4 All Rights Reserved.