スターリング数と多重分割を計算する

ベル三角形によるベル数の計算

ベル三角形によるベル数の計算

ベル三角形を使いベル数を計算するプログラム

ベル数の漸化式よりも簡潔に分割数を計算することができるベル三角形(Atkin's array)を使って、ベル数を計算しその分割を生成します。

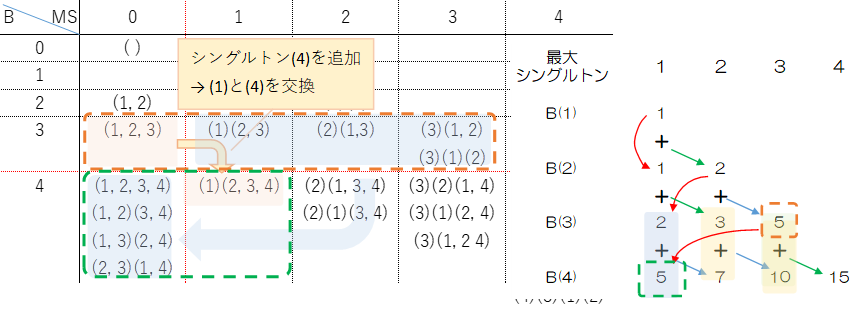
ベル三角形は図の、各行の右端（黄色い部分）がその行の番号に対応したベル数になります。

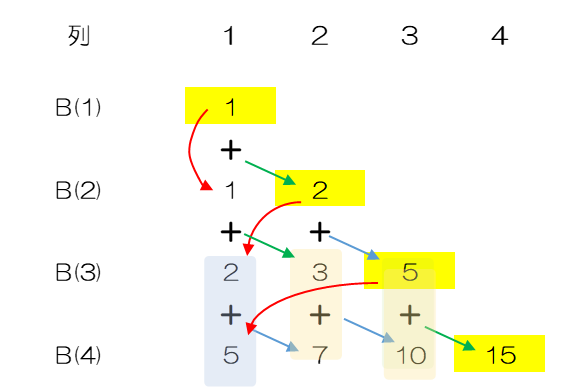
B(1)=1,B(2)=2,B(3)=5,B(4)=15と正しく計算されています。根拠は後に回すとして、ここでは計算の手順を確認します。

B(1)=1からはじめ、B(2)の1列目はB(1)をそのまま転記します（赤い矢印）。

B(2)の2列目はB(1)=1とB(2)=1の1列目を合計して2となり（緑の矢印）、B(2)になります。

B(3)は飛ばしてB(4)を見ると計算方法が分かります。

1列目はB(3)の分割数5を転記します（赤い矢印）。

2列目は③で転記した5とB(3)の1列目=2を合計して7になります。

3列目は④の7+B(3)２列目の3を足して10になります。

4列目は⑤の10B(3)3列目の5を足して15になりB(4)になります。

このようにB(5)以降も各行の左端は前の行の右端にあるベル数をそのまま転記し、2列目以降は同じ行の1つ左の値と、1つ上の行で1つ左の値の和を計算します。前項の漸化式はかなり複雑な計算が必要ですがベル三角形は非常に少ない計算量で、ベル数を次々と計算することができます。

こんな簡単な計算でなぜ複雑なベル数を計算するのかはさておいて、ベル三角形を生成するプログラムを作成します。ここではリストatkins_arrayを使いベル三角形を累積し、各nの行はnext_bellで計算します。

[[1],
 [1, 2],
 [2, 3, 5],
 [5, 7, 10, 15],
 [15, 20, 27, 37, 52],
 [52, 67, 87, 114, 151, 203],
 203

2.　B(1)=1なので、リストatkins_arrayを[1]で初期化し、以降B(2)から計算を始めます。

3.　B(2)から、B(n)までのベル数を求めるため残りn-1回ループします。

4.　B(i)を計算するnext_bellの0番目の要素は、B(i-1)、つまり1つ前のベル数で初期化します。

5.　next_bellの2列目以降は、前の行B(i-1)の1列目と今の行B(i)の1列目の和を追加します。以降i=nになるまで同じ計算を繰り返します。

6.　1行の計算が終わるとatkins_arrayに追加します。最終的にatkins_arrayがベル三角形になります。

9.　nに該当するベル数は、ベル三角形のatkins_array[-1][-1]（最後の行の右端の値）になります。

ベル数を計算する関数

プログラㇺ#19はB(n)を計算するときB(0)からB(n-1)までをリストとして保持し、計算結果の出力にもひと手間かかります。ところが、ベル三角形の良いところはB(i)を計算するためにはB(i-1)の行だけがわかっていれば計算できるので、B(i-2)以前の行は消してしまっても問題ないということです。そこでB(i-1)だけの行をprevとして保持し、prevをもとにリストatkins_arrayを生成するように変更します。

203

2.　B(1)=1なので1でリストprevを初期化します。

4.　新しく計算するatkins_arrayの0番目の要素（左端）にB(i-1)をセットします。

5.　それ以降は前の行と今の行の和を追加していきます。

ベル三角形でベル数を計算することができる理由

最大シングルトンによる分類

ベル数では、分割の中で要素が1つだけのものをシングルトン( singleton)といい、シングルトンのなかで最も大きなものを最大シングルトンといいます。

表は列をB(0)からB(4)まで、行見出しは最大シングルトンで整理したものです。例えばB(4)行の0列目は全ての分割が複数の要素を持つもので、シングルトンが無いので最大シングルトンは0になり4つの分割があります。一方。②はB(3)で1列目はシングルトンが(1)だけなので、最大のシングルトンは1になります。同様に、2列目の最大シングルトンは2になります。3列目は(3)(1,2)はシングルトンが3だけですが、(3)(1)(2)はシングルトンが3つありますが最も大きいので、いずれも最大シングルトンは3になります。

最大シングルトンの考え方が分かったうえで興味深い1対1対応を探します。

全単射１　B(n-1)で最大シングルトンが1～n-1 ⇔B(n)で最大シングルトンなし

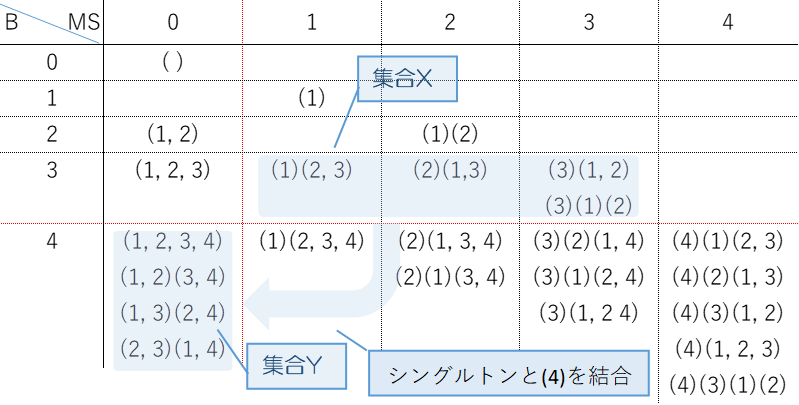
B(3)で最大シングルトンが1から3までの分割を集合X 、B(4)で最大シングルトン0の分割を集合Yとします。Xのシングルトンに(4)を結合し、もし、Xに複数のシングルトンがあった場合は(4)を含めて全て結合します。するとB(4)の分割でなおかつシングルトンはなくなるので集合Yに対応付けられます。逆に集合Yから4を削除し、4と同じ分割にあった要素は全てシングルトンに分割します。例えば(1,3)(2,4)は4を削除するとB(3)で最大シングルトンが2の(1,3)(2)になります。(1,2,3,4)は4を削除すると(1,2,3)になりますが、この3つをシングルトンに分割します。この結果、B(3)で、なおかつ最大シングルトンが1から3の集合Xに対応付けられます。つまりお互いに逆写像を持つことになるので一対一対応になり個数は等しくなります。

全単射2-1　B(n-1)で最大シングルトンが0～n-1 ⇔B(n)で最大シングルトンn

B(3)で最大シングルトンが0から3までの分割を集合X、B(4)で最大シングルトンが4の分割を集合Yとします。集合Xにシングルトン4を追加すると集合Yになり、集合Yの各要素からシングルトン4を削除すると集合Xになります。お互いに逆写像を持つので一対一対応になります。

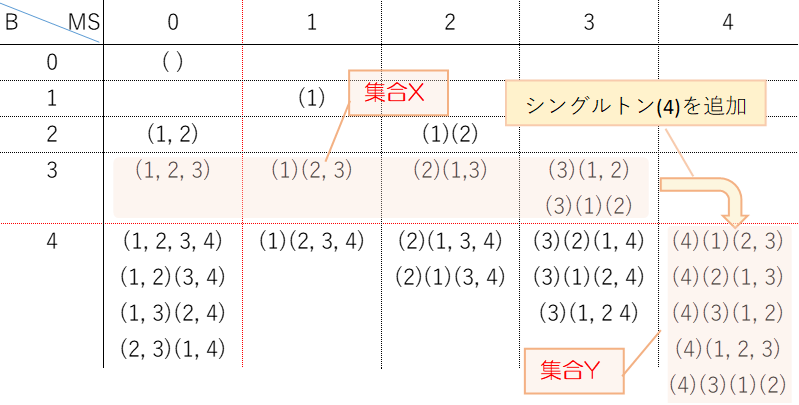
全単射2-2　 B(3)で最大シングルトンが0～k-1 ⇔B(4)で最大シングルトンk

さらに、B(3)で最大シングルトンが0～k-1の分割を集合X、B(4)で最大シングルトンがkの分割をYとします。図はk=2を例にします。XからYへの対応は、シングルトン4をいったん追加して、4とkを交換します。一方YからXへの対応はkと4を交換してシングルトン4を削除します。これも一対一対応になります。

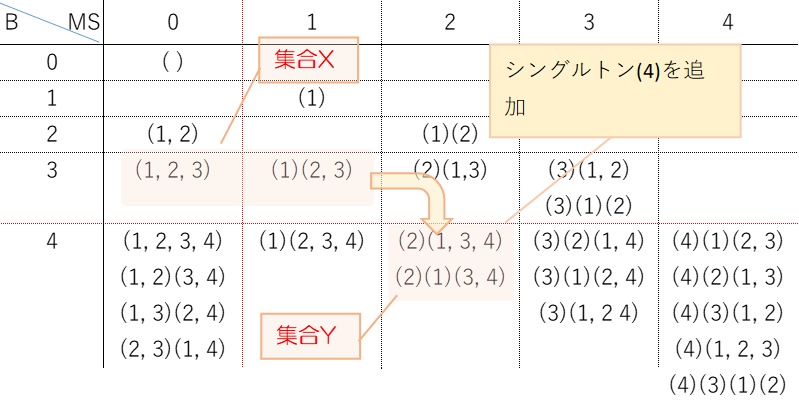
さらに、B(3)で最大シングルトンが0～2の分割を集合X、B(4)で最大シングルトンが3の分割をYとします。XからYへの対応は、シングルトン4をいったん追加して、4と1を交換します。一方YからXへの対応は1と4を交換してシングルトン4を削除します。これも一対一対応になります。

以上、3つの一対一対応を取り上げましたが、2-1は2-2のn=kの特殊なものとすると２つの対応として考えられます。

2つの一対一対応を使ってベル三角形の仕組みを解明

ベル三角形に並んでいる数字は、ベル数ごとの最大シングルトンを累積したものです。

例えばB(3)を見ると、1列目はシングルトンが無しか、最大シングルトンが1の個数です。2列目は1列目に最大シングルトンが2の個数を追加（累積）します。さらに3列目は最大シングルトンが3の個数を累積します。結果として3列目はシングルトンが無いものから3までの個数が累積されるのでベル数が計算されます。

B(4)については、ルールⅠにより、0列目はB(3)の最大シングルトンが1から3、1列目はB(3)のシングルトン無しの個数になるので、合計して5となり表の1列目の値になります。

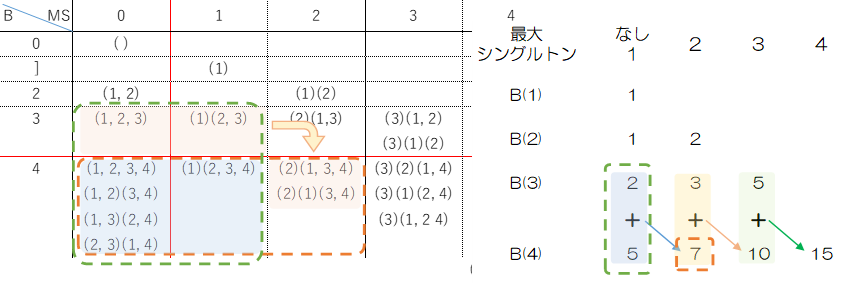
B(3)には3つの数字が並んでいますが、2はシングルトンが無いか最大シングルトンが1の分割の個数です。

3は上記に加え、最大シングルトンが2の個数です。最後の5は上記に加え、最大シングルトンが3のものです。このため3番目の5はシングルトンが無いか、最大シングルトンが1,2,3の個数になるためB(3)と等しくなります。このことからベル三角形の各行の右端はベル数が表示されます。

B(4)の左端は、2はシングルトンが無いか最大シングルトンが1の分割の個数を表示しますが、④からB(3)と等しいので前の行の右端をそのまま転記します。２列目はこれに最大シングルトンが2の個数を足し込みます。この足し込む数字は④から前行の左端と等しくなります。つまり、左端の5と前行の左端の2の合計になります。

このようにしてベル三角形の仕組みを解明することができました。