分割数を写像から考える

不定方程式を使い分割数を生成する

分割数の考え方

これまで、写像の考え方を使い集合N、Kともに、またはいずれかに区別があるものを扱ってきました。最後に、集合N、Kともに区別がないものを考えます。区別をする必要が無いことから簡単かと思いきや、実は非常に複雑で奥深いものがあります。それではさっそく、次の問題を考えます。

問題1

整数6をいくつかの正の整数の和であらわしてください。ただし、1+2+3、2+3+1などは区別せず、１つの組み合わせと考えます。

答えは、次の11通りになります。

(1+ 1+ 1+ 1+ 1+ 1)

(2+ 1+ 1+ 1+ 1)

(3+ 1+ 1+ 1)、(2+ 2+ 1+ 1)

(4+ 1+ 1) 、(3+ 2+ 1)、 (2+ 2+ 2)

(5+ 1)、(4+ 2)、(3+ 3)

(6)

このような1つ１つの整数の和の組み合わせ、例えば3+ 2+ 1を分割 (partition)といい、3,2や1のように分割を構成する個々の正の整数を和因子(part)といいます。また、正の整数nに対する分割の個数は分割数(partition number)といいp(n)であらわします。例えばp(6)=11 (partition number of 6 is 11)というように表します。分割は3+ 2+ 1のように大きいもの数から小さい数の順（降順）に並べるのが一般的で、今後、(3, 2, 1)のように表すこととします。

たかだか6程度の整数でも、思いつくままに書き出していたのでは正確に数え上げるのは容易ではありません。そこで図表1のように、写像を使って整理します。例えばk=3の(3,2,1)の分割は、図表1の左側のように表現することができます。

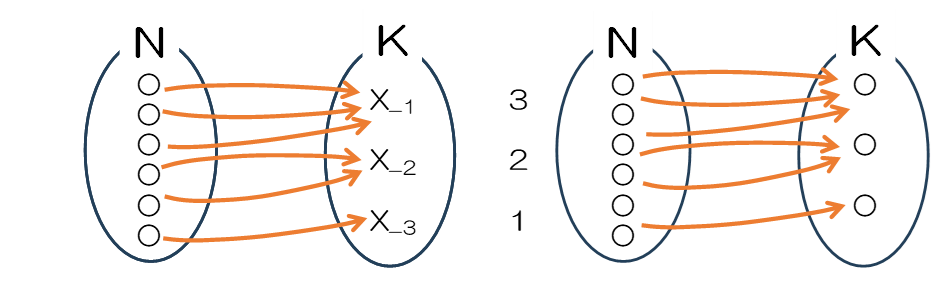
この写像は図表の②の不定方程式と似ていることに気づきます。不定方程式では$x_1+x_2+x_3 \lt6\quad(x_i\geqq1)$を満たす組み合わせを求めました。分割と異なるのは、集合K$x_1,x_2,x_3$を区別しているので、3+2+1と1+2+3は別の組み合わせとして計算しているところです。そこで、分割を求めるためには不定方程式の組み合わせを求め、集合Kの区別なしの分割に変換すればよいことになります。

不定方程式によるリストの作成

1つの例としてindefinite_surjective_func関数を使い、$x_k=3$の和を表す不定方程式の解の組み合わせを生成します

不定方程式の関数を使って和がnになるk個の整数を求める

def indefinite_surjective_func(k, n):
array = [[]]
for kth in range(k):
temp = array
array = []
for elm in temp:
if kth < k-1:
for nth in range(1, n-k+2): # range(n+1)
new_elm = elm + [nth]
if sum(new_elm) < n: #<=
array.append(new_elm)
else:
break
else:
array.append(tuple(elm + [n-sum(elm)]))
return array
n = 6
k = 3
indefinite_surjective_func(k, n)

[(1, 1, 4),
 (1, 2, 3),
 (1, 3, 2),
 (1, 4, 1),
 (2, 1, 3),
 (2, 2, 2),
 (2, 3, 1),
 (3, 1, 2),
 (3, 2, 1),
 (4, 1, 1)]

20.　k個の正の整数の和がnになる不定方程式を求めるのでn=6,k=3としてindefinite_surjective_func関数を呼び出します。

$x_1+x_2+x_3 \lt6\quad(x_i\geqq1)$の不定方程式の解の個数は$\_k H_{n-k} =\ _{n-1} C_{n-k}=\ _{n-1} C_{k-1}$とります。よってk=3び場合は

$x_1+x_2+x_3 = n \\ x_i\geqq 1\quad(i=1,2,\cdots,k)$

$\ _6 H_{6-3} =\ _{5} C_{2}=10$となり計算結果が正しいことがわかります。

不定方程式の解の組み合わせを生成することができました。次に増加関数の考え方を使い集合Kを区別なしに変換しますが、分割は要素を大きな順番に並べるのでinccreasing_map_funcを少し変更し、2番目の引数をreverse=Trueとすることで、降順の要素を抜き出すことができるようにします。もちろん、この関数は昇順で使うことの方が多いので、reverseを指定しなければFalseとなり昇順の要素を抜き出すようにします。

不定方程式から降順の分割だけを抜き出す

def increasing_map_func(inversed_list, reverse=False):
array=[]
for elm in inversed_list:
for i in range(len(elm)-1):
if (elm[i] < elm[i+1]) if reverse else (elm[i] > elm[i+1]):
break
else:
array.append(elm)
return array
print(increasing_map_func(indefinite_list,reverse=True ))

[(2, 2, 2), (3, 2, 1), (4, 1, 1)]

5.　Pythonでは次のような三項演算子を使うことにより、状況に応じてifを使った条件式を切り分けることができます。

条件式が真のときに返す値 if 条件式 else 条件式が偽のときに返す値

このことにより、if reverseでrverse==Trueかを聞き、条件を変更することができます。

当初抜き出したように3つの分割を作成することができました。

分割数の難しさ

分割数を作成したり個数を求めたりする方法を一般化します。

不定方程式で求めた組み合わせの個数から分割数を求める計算方法を一般化します。スターリング数と同じようにk!で割ればよいような気がします。

例えば、n=6,k=3の場合、(3,2,1),(4,1,1),(2,2,2)の3種類の分割があります。これらのうち前2つについて集合Kについてラベル無しに変換すると図の通りになります。

ますが、分割数の場合は同じになるので、同じ3個の組み合わせでも、一括して3!とするのではなく重複度に応じて割り返す数が変わってきます。

例えば(3,2,1)の分割は集合Nが区別ありの場合も、区別なしの場合も3!通りが1つの分割に集約されます。これに対して(4, 1, 1)の分割はスターリング数では、(A)(B)(C,D,E,F)と(B)(A)(C,D,E,F)は別のものと認識し3!通りと変わりませんが、分割数では1の分割が２つあるので、3!/2!個を1つに集約します。さらに図にはありませんが、(2,2,2)に至っては3!通りを1つの分割にするように場合分けをする必要があります。ここが分割数の難しさですが、とんでもなく奥が深い世界が待っています。

K=3以外の場合も計算

はじめに計算した分割にはk=3だけでなく、k=1からk=6までの分割が考えられます。

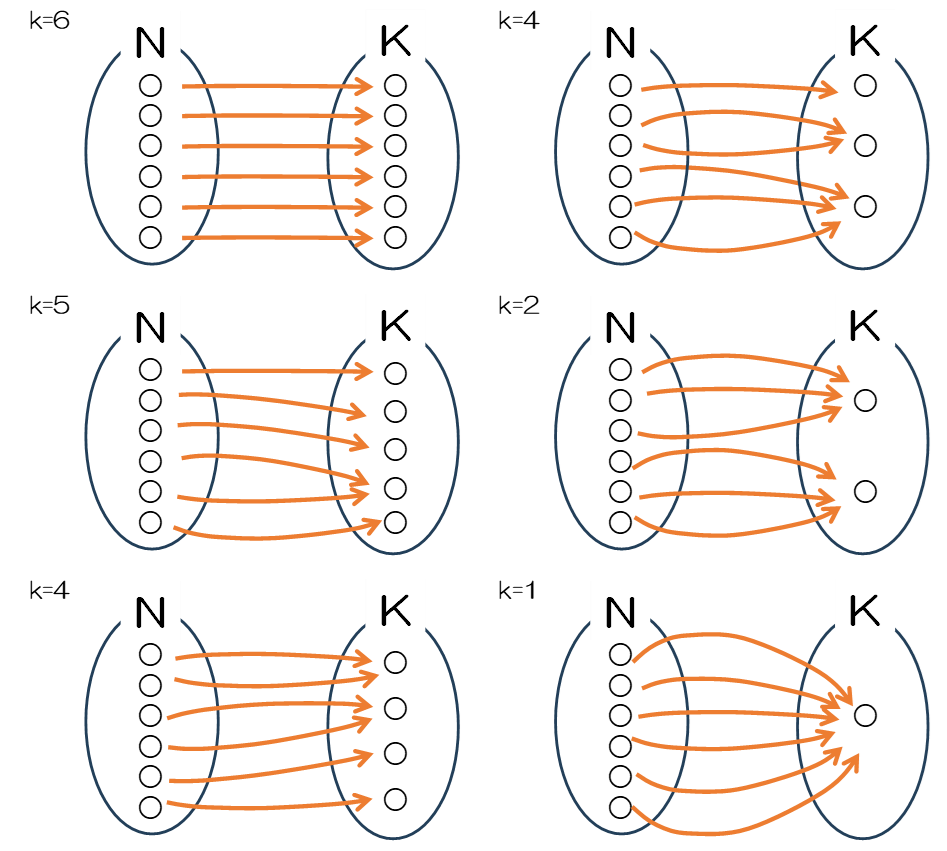
図表1を眺めていると、を使い、のようにn=6、k=6の制約なしのパターンとなり、k=1からk=6までに分類します。図1を眺めていると、不定方程式を使いkの個数ごとに組み合わせを生成し、$x_k$について増加写像の考え方を使いラベル無しの分割に変換します。

不定方程式の結果をわかりやすく集計

分割数に近い結果を得ることができましたが、まだ1+2+3、2+3+1など別の組み合わせとして数えています。そこで、増加写像の考え方を使い、ラベル無しの分割に変換します。和因子の個数は1から6まで考えられるので、それぞれの個数を計算するため、不定方程式の関数を使って全射の条件で1つ1つ組み合わせを生成します。このためk=1からk=6までindefinite_surjective_func関数を適用し、結果はリストindefinite_listに追加します。

不定方程式で要素数が1から6まで計算

indefinite_list = []
for i in range(1, n+1):
indefinite_list.append(indefinite_surjective_func(i, n))
cnt = 0
for categorized_elm in indefinite_list:
print(categorized_elm, len(categorized_elm))
cnt += len(categorized_elm)
print('合計',cnt,'個')

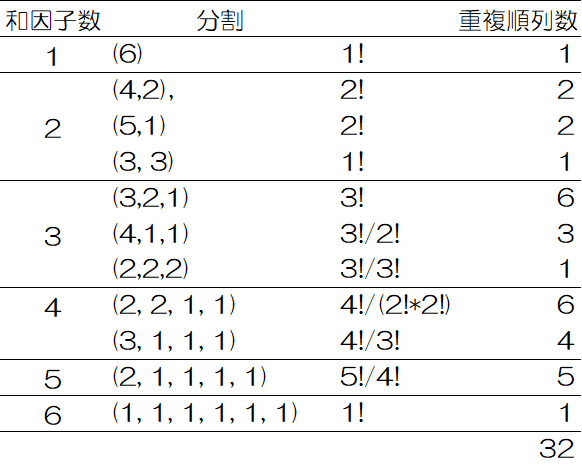
[(6,)] 1
[(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)] 5
[(1, 1, 4), (1, 2, 3), (1, 3, 2), (1, 4, 1), (2, 1, 3), (2, 2, 2), (2, 3, 1), (3, 1, 2), (3, 2, 1), (4, 1, 1)] 10
[(1, 1, 1, 3), (1, 1, 2, 2), (1, 1, 3, 1), (1, 2, 1, 2), (1, 2, 2, 1), (1, 3, 1, 1), (2, 1, 1, 2), (2, 1, 2, 1), (2, 2, 1, 1), (3, 1, 1, 1)] 10
[(1, 1, 1, 1, 2), (1, 1, 1, 2, 1), (1, 1, 2, 1, 1), (1, 2, 1, 1, 1), (2, 1, 1, 1, 1)] 5
[(1, 1, 1, 1, 1, 1)] 1
合計 32 個

2～3.　nに対して1からnまでのkについてindefinite_list.append関数を適用し、その結果をリストindefinite_listに追加します。

n=6,k=3の場合、不定方程式の解の組み合わせは$\ _{n-1} C_{k-1}=\ _5 C_3=10$で計算しました。よって、k=1からk=6まで計算すると要素数ごとの個数と総合計は次の式から計算することができます。

$\sum\limits _{k=1}^{n} \ _{n-1} C_{k-1}=\sum\limits _{k^{\prime}=0}^{n^{\prime}} \ _{n^{\prime}} C_{k^{\prime}} = \ _{n^{\prime}} C _0 + \ _{n^{\prime}} C _1+ \ _{n^{\prime}} C _2+ \ _{n^{\prime}} C _3 + \cdots \ _{n^{\prime}} C _{n^{\prime}} = 2^{n^{\prime}}=2^{n-1}$

したがって

$\ _5 C_0+\ _5 C_1+\ _5 C_2+\ _5 C_3+\ _5 C_4+\ _5 C_5=1+5+10+10+5+1=32=2^5$

このことは次の図で見るとイメージできると思います。6個の区別の無い集合Nの要素に対し、0個から5個の「しきり」をつくります。例えば、①の1+2+3は2,4,5番目の「しきり」に＋を入れます。また②のように6の分割は＋をどこにも入れません。

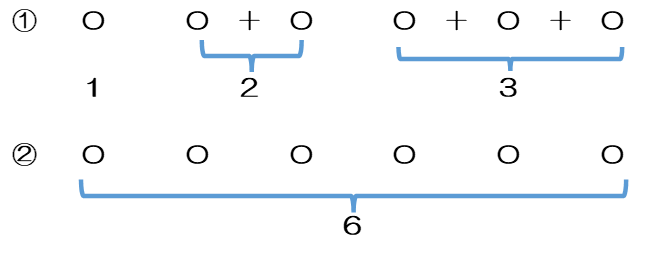
このように5個の「しきり」に＋を入れる入かれないかを自由に選ぶことができるので$2^{n-1}=2^5$個になることがわかります。

図らずも、分割数を計算する過程で二項定理の関係を見出すことができます。

増加写像を応用して分割数を降順にする

分割数は集合Kについては区別しない組み合わせなので、1+2+3、2+3+1など不定方程式では別のものとして数えていたものを増加関数の考え方を使って集約します。ただし、今回は分割は大きなものから並べるので、降順にするため、increasing_map_funcを降順のものを抜き出すようにして適用します。

それぞれの組を降順にして集計しやすくする

cnt = 0
for elm in indefinite_list:
partition = increasing_map_func(elm, reverse=True)
print(len(partition),'個', partition)
cnt += len(partition)
print('合計',cnt,'個')
print('合計',cnt,'個')

1 個 [(6,)]
3 個 [(3, 3), (4, 2), (5, 1)]
3 個 [(2, 2, 2), (3, 2, 1), (4, 1, 1)]
2 個 [(2, 2, 1, 1), (3, 1, 1, 1)]
1 個 [(2, 1, 1, 1, 1)]
1 個 [(1, 1, 1, 1, 1, 1)]
合計 11 個

5.　elmのiよりi+1番目の値が大きくなると降順にならないのでbreakしてarrayに追加しないようにします。これ以外はincreasing_map_funcと同じです。

1つ１つの組み合わせにincreasing関数をreverse=Trueとして適用して、降順になっていないものは削除します。この結果、区別なしの分割の要素の個数ごとに出力します。最初に求めた組み合わせと同じように11個になり、はじめに数え上げた個数と一致します。

SymPyライブラリによる分割数の表示

PythonではSymPyライブラリを使い、分割数の一覧を作成したり個数を計算したりすることができます。これまでの計算結果を確認します。

分割数を計算する関数

分割数だけであれば、SymPyライブラリのpartition関数を使って計算することができます。

SymPyライブラリで分割数の計算をする

from sympy import partition
sym_partition_cnt = partition(n)
print(sym_partition_cnt)

1.　stirling関数はSympyライブラリのfunctions.combinatorial.numbers サブモジュールからimportします。

1. partition関数に正の整数を適用すると、分割数を計算することができます。

SymPyライブラリのpartiton関数で、nに応じた分割数の数を計算することができます。N=6の場合11個ということで、計算結果に合致します。

分割を生成する関数

分割はsympyライブラリのpartitions関数を使い生成することができます。

SymPyライブラリで分割数の計算をする

from sympy.utilities.iterables import partitions
sym_partition_dict = list(partitions(n))
print(sym_partition_dict)

 [{6: 1}, {5: 1, 1: 1}, {4: 1, 2: 1}, {4: 1, 1: 2}, {3: 2}, {3: 1, 2: 1, 1: 1}, {3: 1, 1: 3}, {2: 3}, {2: 2, 1: 2}, {2: 1, 1: 4}, {1: 6}] 11

1.　 partitions関数はSymPyライブラリのsympy.utilities.iterablesモジュールからインポートします。

2.　 partitions関数の返り値はジェネレータという特殊な形式なので、list関数で出力結果をリストに変換します。

ただし、出力結果のうち個々の分割は辞書形式となり少し見づらいので、リスト形式に変換します。配列result_listに辞書形式の分割をリストに変換して挿入します。

辞書形式で求めた分割数をリストに変換する

for elm in sym_partition_dict:
result_list=[]
for key, value in elm.items():
result_list.extend([key] * value)
print(result_list)

[6]
[5, 1]
[4, 2]
[4, 1, 1]
[3, 3]
[3, 2, 1]
[3, 1, 1, 1]
[2, 2, 2]
[2, 2, 1, 1]
[2, 1, 1, 1, 1]
[1, 1, 1, 1, 1, 1]

3.　辞書形式の分割から、分割の要素をkey,分割の中の個数をvalueとします。

4. result_listにはkeyの要素をvalue個だけ追加します。

このようにリストに変換することができました。合計11件でこれまでの計算結果と一致していることがわかります。

n=1から決められた数までの分割数を連続して生成する関数

分割を生成する関数の考え方

前節で不定方程式から分割を生成しましたが、ここでは直接に生成するプログラムを作成します。このとき、分割数の左端の最大の和因子に注目する全単射を見出すことにより、面白いプログラムを作ることができます。

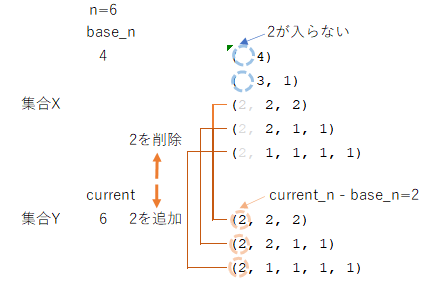
6の分割数11個を集合Xとします。これに対し、集合Xの分割の最も大きな数字（左端）を削除した分割を集合Yとします。例えば、集合Xの分割(2, 2, 1, 1)は、集合Yの(2, 1, 1)に対応します。(2, 1, 1)は4の分割になるので集合Yは6-2=4の分割数となります。このため、4の分割は全て集合Yの部分集合になるような気もしますが、実はそうではありません。例えば、(3,1)は4の分割数の1つですが、左端に2を追加すると降順であるという前提が崩れてしまいます。

少し面倒ですが、集合Ｙを別の視点から見ると、6以下のiに対して6-iの分割でなおかつ最大の和因子がiであるものと定義することができます。ここで、集合Yから集合Xへの対応を考えます。(2, 1, 1)は4の分割なので6との差2を左に追加しても降順であるとの分割を満たすので集合Xの(2, 2, 1, 1)に対応付けられ写像であるといえます。

このことから集合Xと集合Yは全単射（一対一対応）といえます。

分割数を生成するプログラム

この考え方から分割数を生成するプログラムを作成します。最終的な6の分割数は[(6),(5,1)・・・]のようにリストのなかに分割数がタプルとして埋め込まれるようにしますが、全単射の考え方を取り入れるため、1から５までの分割数を順次計算し、その結果を積み上げていくので3次元の配列になります。

関数名はpartition_func(n)とし、引数は求めたい分割のnとします。今計算している分割をcurrent_n、参照している分割をiとして定義するので、削除、追加をするk= current_n - iとなります。

和因子の最大値を順次挿入することにより分割数を計算

def partition_func(n):
array = [[()]]
for current_n in range(1, n+1):
new_array = []
for i in range (current_n):
for elm in array[i]:
if elm == () or elm[0] <= current_n - i:
new_array.append((current_n - i,) + elm)
array.append(new_array)
return array
partition_func(6)

[[()],
 [(1,)],
 [(2,), (1, 1)],
 [(3,), (2, 1), (1, 1, 1)],
 [(4,), (3, 1), (2, 2), (2, 1, 1), (1, 1, 1, 1)],
 [(5,), (4, 1), (3, 2), (3, 1, 1), (2, 2, 1), (2, 1, 1, 1), (1, 1, 1, 1, 1)],
 [(6,),
  (5, 1),
  (4, 2),
  (4, 1, 1),
  (3, 3),
  (3, 2, 1),
  (3, 1, 1, 1),
  (2, 2, 2),
  (2, 2, 1, 1),
  (2, 1, 1, 1, 1),
  (1, 1, 1, 1, 1, 1)]]

2.　n=0の場合は空集合として定義します。

3.　以下で、nまで順次、分割数を求めます。

4.　作成中の分割数はnew_array に積み上げていきます。

5.　作成中の分割より小さい分割をelmに代入し、順次チェックします。

6.　iの分割の中で集合Ｙに当てはまるものについて、k= current_n - iをnew_arrayに追加します。

7.　elm == ()という条件は、n=1を作成するときelmがブランクであるためです。or条件の左側がTrueになるとorの右側は評価されません。このためelm[0]はエラーになりません。

この処理を、全て行って終了となります。

例えば、partition_func(6)を呼び出すと、数字6をさまざまな整数の和に分割したパターンがリストとして返されます。

分割をこんな簡単なプログラムで生成することができるのは驚きです。しかし、処理の中身を見るとnの分割数を求めるのに、毎回1からn-1までの分割数を1つ１つ見に行くのでかなりの無駄が生じるので、分割の個数p(n)だけを計算するのであればもっと簡単な方法を模索していきます。

補助関数の導入

補助関数の意味と種類

補助関数の考え方

p(n)のように直接計算するのが難しい時には、計算しやすくするための補助関数(auxiliary function)という別の関数を使う手があります。

補助関数の1つの例としてp(n)を和因子の個数kで分類し、p(n ,k)とする方法があります。補助関数p(n, k)で個数を計算したのち、本丸のp(n)を落としに行く作戦です。例えばn=6、k=3の場合、(4, 1, 1)、(3, 2, 1)、(2, 2, 2)の3つの分割があります。分割の補助関数の値はSymPyライブラリのnT関数を使って計算することができます。

SymPyライブラリのnT関数で分割数の補助関数を計算する

from sympy.functions.combinatorial.numbers import nT
partition_count = nT(6, 3)
partition_count

1.　 nT関数はSympyライブラリのsympy.functions.combinatorial.numbers サブモジュールからimportします。

SymPyライブラリからnT関数をimportします。

上記の3つの分割を正しく計算できています。

補助関数の大体の感覚をつかむため、nT関数を使いn=10、k=10までの一覧表を作成します。配列arrayに分割数を代入し、print_table関数を使い出力します。print_table関数は配列と、表の列の幅を引数として、arrayの値と行の合計を表示します。

nT関数を使い、補助関数の一覧表を作成する

def print_table(array, w):
print(f' ' * (w+2), end='')
for k in range(len(array[0])):
print(f'{k:^{w+2}}', end=' ')
print('sigma')
print(f'-' * (w+1), end='+')
for k in range(len(array)+1):
print('-' * (w+2), end='+')
print()
for n in range(len(array)):
print(f'{n:^{w+1}}', end='|')
sigma = 0
for k in range(len(array[0])):
print(f"{array[n][k]:>{w+2}}", end=' ')
sigma += array[n][k]
print(f"{sigma:>{w+2}}")
n=10;k=10
array = [[0]*(k+1) for _ in range(n+1)]
for i in range(1,n+1):
for j in range(1,k+1):
array[i][j]=int(nT(i,j))
print_table(array, 3)

  次のような表になります。

2.　print関数でendを指定すると、その文字列が行末に表示されますが改行はしません。

この表を見ると、次のことがうかがえます。

n
k=1のときはnが大きくても、nが1つの分割にしか分けられないので1
n=kの場合はn個の1が和因子になる分割が1つしか考えられないので1

さらに表を眺めながら補助関数p(n ,k)の正体を探っていきます。

補助関数の漸化式

p(n, k)を直接求めるのは難しいので、漸化式を考えます。例えば、p(9, 3)の分割数は図の通り7になります。このうち最小（最右端）の要素が1かどうかで、2つの集合、集合$X_1$、集合$X_2$に分類します。

集合$X_1$ 9の分割で和因子数3 最小和因子が1

集合$X_2$ 9の分割で和因子数3最小和因子が1以外

8の分割で和因子数2、つまりp(8, 2)の分割を集合Yとし、集合$X_1$との対応を考えます。集合$X_1$の最小和因子（右端）にある1を削除すると合計と和因子数が1ずつ減るので、集合Yに対応します。一方、集合Yの右端に1を追加すると、合計と和因子数が1ずつ減るので$X_1$に対応します。つまり、両者は逆写像を持ち、全単射（一対一対応）になります。一般化すると、P(n, k)のうち最小和因子が1=p(n-1, k-1)となります。

次に6の分割で和因子数3、つまりp(6, 3)の分割を集合Zとし、集合$X_2$との対応を考えます。集合$X_2$の3つの和因子からそれぞれ1ずつを差し引くと、最小和因子（右端）が2以上なので和因子数は3のままで、合計は引いて6になるので集合Zと対応します。一方、集合Zの3つの和因子に1ずつを加えると、和因子数は3のままで合計は9になり$X_2$に対応します。つまり、両者は逆写像を持ち、全単射（一対一対応）になります。一般化するとP(n, k)のうち最小和因子が2以上=p(n-k, k)となります。

まとめる次のような漸化式になります。

補助関数(p,k)を使った分割式の漸化式

k=1 またはn=kのとき　1

$p (n, k)= p(n-1, k-1) + p(n-k, k)$

さっそく漸化式を使い補助関数の個数を求めるプログラムを作成します。漸化式を再帰関数に落とし込むだけです。

漸化式による計算

def partition_r(n, k):
if n < k:
return 0
if k == 1 or n == k:
return 1
return partion_r(n-1, k-1) + partion_r(n-k, k)
partion_r(6, 3)

6.　n=6、k=3を引数として実行すると、n=5、k=2としてさらに関数partition_rを呼び出し優先して実行します。さらにn=4,k=1としてさらに同じ関数が実行されます。

5.　n=4,k=1として関数partition_rを呼び出すと1を返します。この流れを繰り返すと最終的に分割数3が返り値となります。

こんな簡単なプログラムでp(n, k)を計算することができます。

漸化式を使って分割を生成する

さらに、次の漸化式を用いるとp(n, k)の一覧を生成することも可能です。こちらもp(k-1, n-1) 、p(n-k, k)を同じ関数で生成、これに漸化式の処理を加えるようにしています。

漸化式を使って補助関数の分割数を生成する

def pn_list_func(n, k):
if n < k:
return []
if k==1:
return [[n]]
array = []
for elm in pn_list_func(n-1, k-1):
array.append(elm+[1])
for elm in pn_list_func(n-k, k):
array.append([item+1 for item in elm])
return array
pn_list=pn_list_func(9, 3)
pn_list

[[7, 1, 1], [6, 2, 1], [5, 3, 1], [4, 4, 1], [5, 2, 2], [4, 3, 2], [3, 3, 3]]

7.　p(n-1, k-1)の戻り値を１つ1つelmに代入し、右側に1を付け足すことで①の処理ができます。

9.　p(n-k, k) の戻り値を１つ1つelmに代入し、elmの各要素に1を加える処理をしています。

一見すると、なぜ、こんなプログラムで分割を生成することができるのか不思議な感じがしますが、よくプログラムを見ると補助関数による漸化式を素直に反映してくれています。

最大の和因子がKである補助関数を作成する

もう一つの補助関数

補助関数には別の視点で捉えるものとして組み合わせの最大値で分類する方法があり、ここではq(n, k)とします。

n
k=1のときはk個の和因子全ての和因子が1の分割が1つしか考えられないので1
n=kの場合は和因子がkのみの分割が1つしか考えられないので1

q(9 , 3)は和因子の最大値が3で左端に来るもので、図の通り7個あります。これも、前と同じように分けて考えます。

集合$X_1$ 9の分割で最大和因子が3、 2番目に大きな和因子（左から2番目）が3より小さい

集合$X_2$ 9の分割で最大和因子が3、 2番目に大きな和因子（左から2番目）も3

8の分割で最大和因子2、つまりq(8, 2)の分割を集合Yとし、集合$X_1$と対応させます。集合$X_1$の左端にある最大和因子から1を差し引いて2にしても2番目が2以下なので分割として扱うことができ、対応付けることができます。集合Yの左端に1を加えると$X_1$に対応するので、両者は逆写像を持ち、全単射（一対一対応）になります。

6の分割で最大和因が3、つまりq(6, 3)の分割を集合Zとし、集合$X_2$と対応させます。集合$X_2$の左端の和因子を削除しても2番目も３なので、最大の和因子は3のままで集合Zと対応します。一方、集合Zの左端に最大和因子として3を付け加えると$X_2$に対応するので、両者は逆写像を持ち、全単射（一対一対応）になります。

①2番目に大きな和因子（左から2番目）が1番目より小さな分割　

②2番目に大きな和因子（左から2番目）が1番目と同じ分割

①は左端の和因子から1を差し引きます。結果として左端の和因子が2番目の和因子より小さくなることはないのでq(8, 2)と1対1の対応になります。逆にq(8,2)の左端に1を加えると①になり、全単射（1対1の対応）になります。

一方②は左端から1を引いても2番目が3なので降順であるという分割のルールに違反します。そこで、左端の最大値の3の和因子を削除します。②は2番目の和因子も１番目と同じなので、合計は6となり、最大の和因子が3のまま6の分割になりq(6, 3)と全単射（1対1対応）になります。

上記の関係から、次の漸化式を導くことができます。

補助関数qkの漸化式

k=1 またはn=kのとき　1

$q (n, k)= q(n-1, k-1)+q(n-k, k) $

補助関数qkの漸化式

これはp(n, k)と全く同じ漸化式になります。個数を求めるだけであればpartition_r関数と同じになるのでそのまま流用できます。次に、分割数の生成も再帰関数を使うことができます。

漸化式を使って補助関数の分割数を生成する

def qn_list_func(n, k):
if n < k:
return []
if k==1:
return [[1] * n]
array = []
for elm in qn_list_func(n-1, k-1):
array.append([elm[0] + 1] + elm[1:])
for elm in qn_list_func(n-k, k):
array.append([k] + elm)
return array
qn_list = qn_list_func(9, 3)
qn_list

[[3, 1, 1, 1, 1, 1, 1],
 [3, 2, 1, 1, 1, 1],
 [3, 2, 2, 1, 1],
 [3, 2, 2, 2],
 [3, 3, 1, 1, 1],
 [3, 3, 2, 1],
 [3, 3, 3]]

7～8. 　漸化式ｎ左側の部分$q(k-1, n-1) $を組み込んでいます。ここでは一番左側の和因子に1を足すことでq(k,n)の分割を生成しています。同じqn_list_func(n-1, k-1)を引数と変えて呼び出す再帰関数になっています。

9.～10.　漸化式の右側の部分$q(n-k, k)$を組み込んでいます。ここでは、全ての分割の一番左側にkを追加することで、q(k,n)の分割を生成しています。

個数による分類と最大値による分類の1対1対応

前項の漸化式を見るとp(n, k)とq(n, k)の個数が等しいことがわかりましたが、その理由を考えます。

例えばp(6,3)、つまり合計6、和因子数3の1つの例として(4, 2, 1)を取り上げます。この分割に対して、図のようｎ点線を軸に反転させるとq(6,3)つまり、合計は6のままで最大値が3となる(3, 2, 1, 1)の分割になります。さらに、(3, 2, 1, 1)をもう一度反転させると(4, 2, 1)に戻ります。つまり1対1の対応になります。結局p(n, k)とq(n, k)は同じものを見る方向を変えただけということになります。このような関係を共役な分割(partition conjugate）といいます。

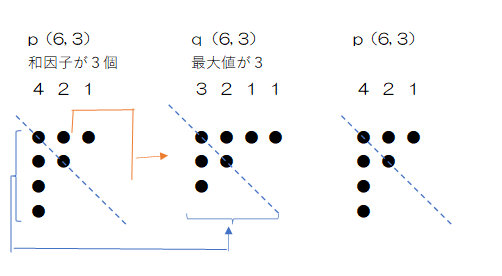
要素数が3の組み合わせ(4,2,1)を最大値が3の組み合わせ(3,2,1,1)に変換する関数を作成します。関数名は共役の英語表記からconjugate_funcとし、引数として分割をリストで渡します。戻り値として共役の分割がリストで返ります。ここでは(4,2,1)を例にして考えます。

p(n,k)からq(n,k)への変換

def conjugate_func(elm):
conjugate_elm = [0] * elm[0]
for item in elm:
for i in range(item):
conjugate_elm[i] += 1
return conjugate_elm
pn=[4, 2, 1]
qn=[3, 2, 1, 1]
print(conjugate_func(pn))
print(conjugate_func(qn))

(3, 2, 1, 1)
(4, 2, 1)

2.　最大の和因子は引数elmの0番目の値（例の場合は4）なので、はじめにその長さのリストを定義し、全て0で初期化します。

3.～4. elmの要素を1つ1つ読み込み、その値の個数だけconjugate_elmの値をカウントアップします。例えば、値が4であればインデックスが0から3の4つ、次の2であれば、0から1までの2つの項目に1を足します。

このことにより、最大値が4のリストを生成することができます。また、この逆の変換をすると元に戻ります。同じ関数を使いp(n,k)とq(n,k)を相互に変換させることができます。このような対応を対合写像（たいごう、ついごうinvolution）といいます。

ここで#12で生成したp(n)の分割にconjugate関数を適用した結果と、#13で生成したq(n)のを比較します。

p(n,k)からq(n,k)への変換の確認

conjugate_p = []
for elm in pn_list:
conjugate_p.append(conjugate_func(elm))
print(qn_list == conjugate_p)
conjugate_q = []
for elm in qn_list:
conjugate_q.append(conjugate_func(elm))
print(pn_list == conjugate_q)

True
True

2次元リストの比較は、単純に比較する場合、内側の要素がすべて正しくても並び順が異なると==演算子で比べた場合等しくなりません。この場合にはsorted関数で並べ替えないと正しい計算結果は得られません。ところが#15ではソートをしなくても等しいとの結果になりました。漸化式を使いpnとqnを生成するととると並び順も含めてしっかりと対応してくれます。このことからp(n,k)=q(n,k)であることを確認することができました。

ぴったりではなく、それ以下という補助関数

分割数がk以下である分割の数　p*(n,k)

これまで、nの分割で和因子数がkのp(n,k)についてみてきました。これに対して和因子数がk個以下とする関数をp*(n k)と定義します。

例えばp*(6,3)は次の3つに分類されます。

①p(6, 3)　 (4, 1, 1), (3, 2, 1), (2, 2, 2)

②p(6,2) (5,1),(4,2),(3,3)

③p(6,1) (6)

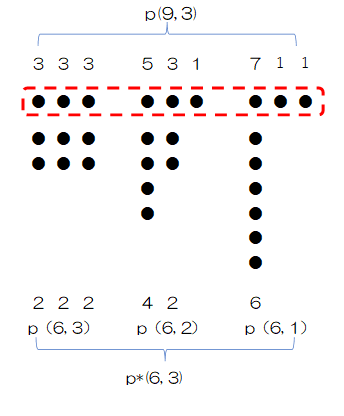
p*(6, 3)を求めるためには、①から③を合計すればよいわけですが、あまりにも芸がありません。そこで、p*(n,k) とp(n,k)との関係を見るために、p(9,3)との関係を考えます。p(9,3)の9はn+k=6+3を意味します。

P(9,3)を次のとおり分類します。

①和因子に1が含まれていない分割　 (5,2,2),(4,3,2),(3,3,3)

②和因子に1が1つ含まれている分割 (6,2,1),(5,3,1),(4,4,1)

③和因子に1が2つ含まれている分割 (7,1,1)

①の代表として(3,3,3)を取り上げます。各和因子を1つずつ差し引くとp(6,3)の(2,2,2)に対応します。(5,2,2),(4,3,2)についても同様です。

②の代表として(5,3,1) を取り上げます。各和因子を1つずつ差し引くと (4,2,0)になり、右側の0を削除するとp(6,2)の(4,2)になります。

③の要素(7,1,1) を取り上げます。各和因子を1つずつ差し引くと (7,0,0)になり、右側の0、2つを削除するとp(6,1)の(6)になります。

逆に、p*(6,3)の要素に対し、和因子数が1,2の場合は右側に0を補い、3つのの配列にし、それぞれ１ずつを加えるとl(9,3)になります。

結果的にp*(6, 3)とp(9, 3)はお互いに逆写像を持ち一対一対応となります。

p(n+k, k)=p*(n,k)

さっそく、pn_list_func関数を使いp*(6,3)とp(9,3)の関係を確かめます。P*(6,3)はp(6,1),p(6,2),p(6,3)を結合してリストpn_63に代入し、p(9,3)も同じ関数で生成してp_93に代入し、分割ごとに比較します。

p(n+k, k)とp*(n,k)の関数

pn_93 = pn_list_func(9, 3)
pn_aster_63 = pn_list_func(6, 1)+pn_list_func(6, 2)+pn_list_func(6, 3)
for i,j in zip(pn_93, pn_aster_63):
print(f'{str(i):<14}{str(j):<14}')

[7, 1, 1]     [6]           
[6, 2, 1]     [5, 1]        
[5, 3, 1]     [4, 2]        
[4, 4, 1]     [3, 3]        
[5, 2, 2]     [4, 1, 1]     
[4, 3, 2]     [3, 2, 1]     
[3, 3, 3]     [2, 2, 2]

3.　pn_93とpn_aster_63をzip関数で要素ごとに組み合わせて出力します。

4.　2つのリストを並べて見やすくするため、列幅を14文字分とします。str関数でリストを

文字列に変換すると列幅を指定することができます。

p(n)とp*(n)の関係が分かったところで、pnを生成するpn_list_func 関数を使い、p*(n)を生成する関数を作成します。pn_list_func関数の引数nをn+kにして呼び出すことにより、p*(n)のもとになるリストを生成することができます。ここから、k個の和因子から1を引き、０になったら削除するよう処理をします。

p*(n)のリストを生成する

def pn_aster_list_func(n, k):
array = []
for elm in pn_list_func(n+k, k):
new_elm = []
for item in elm:
if item > 1:
new_elm.append(item-1)
array.append(new_elm)
return array
for i,j in zip(pn_aster_list_func(6, 3), pn_aster_63):
print(f'{str(i):<18}{str(j):<16}')

[6]           [6]           
[5, 1]        [5, 1]        
[4, 2]        [4, 2]        
[3, 3]        [3, 3]        
[4, 1, 1]     [4, 1, 1]     
[3, 2, 1]     [3, 2, 1]     
[2, 2, 2]     [2, 2, 2]

2.　全体の配列はarrayに、また4.にあるように個々の分割はnew_elmというリストにします。

3.　 pn_list_func(n+k,k)で生成したリストに対し、和因子が1であれば何もせず、1よりおおきければ1を引いてnew_elmに追加することで、p*(n, k)の分割を生成することができます。

最大の和因子がk以下の分割の個数　q*(n,k)

例えばp*(q,3)は次の3つに分類されます。

①q(6, 3)　 (3, 1, 1, 1) (3, 2, 1)(3, 3)

②q(6,2) (2, 1, 1, 1, 1)(2, 2, 1, 1)

③q(6,1) (1, 1, 1, 1, 1, 1)

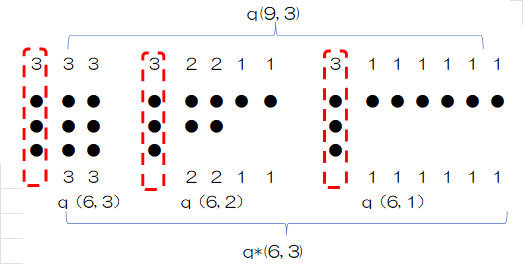
q*(n,k) とq(n,k)との関係を見るために、q(9,3)との関係を考えます。q(9,3)の9はやはりn+k=6+3を意味します。

q(9,3)を次のとおり分類します。

①2番目に大きな和因子が3の分割　(3, 3, 1, 1, 1) (3, 3, 2, 1)(3, 3, 3)

②2番目に大きな和因子が2の分割 (3, 2, 1, 1, 1, 1)(3, 2, 2, 1, 1)

③2番目に大きな和因子が1の分割 (3, 1, 1, 1, 1, 1, 1)

①の代表として(3,3,3)を取り上げます。最大和因子（左端）の3を削除するとq(6,3)の(3,3)に対応します。(3, 1, 1, 1),( 3, 2, 1)についても同様です。

②の代表として(3, 2, 2, 1, 1) を取り上げます。最大和因子（左端）の3を削除すると、q(3,2 ) の(2, 2, 1, 1)になります。

③の要素(3, 1, 1, 1, 1, 1, 1) を取り上げます。最大和因子（左端）の3を削除すると、q(3,1 ) の(1, 1, 1, 1, 1, 1)になります。

逆に、q*(6,3)の要素に対し、最大和因子（左端）に3を追加するとq(9,3)になります。

結果的にq*(6, 3)とq(9, 3)はお互いに逆写像を持ち一対一対応となります。

さっそく、pn_list_func関数を使いq*(6,3)とq(9,3)の関係を確かめます。q*(6,3)はq(6,1),q(6,2),q(6,3)を結合してリストqn_63に代入し、q(9,3)も同じ関数で生成してp_q3に代入し、分割ごとに比較します。

q(9,3)とq*(6,3)の関係を確かめる

qn_93 = qn_list_func(9, 3)
qn_aster_63 = qn_list_func(6, 1)+qn_list_func(6, 2)+qn_list_func(6, 3)
for i,j in zip(qn_93, qn_aster_63):
print(f'{str(i):<26}{str(j):<26}')

[3, 1, 1, 1, 1, 1, 1]     [1, 1, 1, 1, 1, 1]        
[3, 2, 1, 1, 1, 1]        [2, 1, 1, 1, 1]           
[3, 2, 2, 1, 1]           [2, 2, 1, 1]              
[3, 2, 2, 2]              [2, 2, 2]                 
[3, 3, 1, 1, 1]           [3, 1, 1, 1]              
[3, 3, 2, 1]              [3, 2, 1]                 
[3, 3, 3]                 [3, 3]

比べます。

q*(n, k)=q(n+k,k)

qnとq*nの関係を確認する

def qn_aster_list_func(n, k):
array = []
for elm in qn_list_func(n+k, k):
array.append(elm[1:])
return array
for i,j in zip(qn_aster_list_func(6, 3), qn_aster_63):
print(f'{str(i):<24}{str(j):<24}')

[1, 1, 1, 1, 1, 1]      [1, 1, 1, 1, 1, 1]      
[2, 1, 1, 1, 1]         [2, 1, 1, 1, 1]         
[2, 2, 1, 1]            [2, 2, 1, 1]            
[2, 2, 2]               [2, 2, 2]               
[3, 1, 1, 1]            [3, 1, 1, 1]            
[3, 2, 1]               [3, 2, 1]               
[3, 3]                  [3, 3]

3.　 qn_list_func(n+k,k)で生成したリストに対し、最大和因子（左端）を削除してarrayに追加します。

def qn_aster_list_funcの方が、分割の左端を削除するだけなので処理が簡単なのがわかります。

漸化式を応用して分割数を計算する

分割数の計算

漸化式を使った分割数を計算する関数をまとめます。この関数では、引数にnのみを指定した場合は分割数、(n,k)を指定した場合は補助関数、aster=Trueとしたときはk個以下の合計を計算することとします。

漸化式を使って分割数の個数を計算する

def partition(n, k=None, aster=False):
if aster:
n += k
elif k is None:
k = n
n = 2 * n
if n < k:
return 0
if k == 1 or n == k:
return 1
return partition(n-1, k-1) + partition(n-k, k)
print(partition(6,3))
print(partition(6,3,aster=True),partition(6,1)+partition(6,2)+partition(6,3))
print(partition(6),partition(6,6,aster=True))

3
7 7
11 11

2.　asterがTrueの場合、nにkを加え、n+kとします。なお、if aser はif aster=Trueと同じことです。

3.　kに値が指定されない場合は、分割数と考え、k=n,n=2*nとします。このように引数に何も指定されない場合に、具体的な数値ではなく、計算結果を初期値として大雄するとときにはk=Noneというように指定します。

4.　ある値がNoneかを判断するときはis演算子を使います。

==値の等価性を比較するのに対し、isは同じオブジェクトかどうかを判断します。

このような、すっきりとした関数で分割数を計算することができるのは驚きです。

漸化式を使った分割の生成

p(n,k)関数の応用

p(n,k)を使い、漸化式を使って分割を生成する関数を作成ます。pn_list_func関数とpn_aster_list_funcは再掲です。新規に作るのはpartition_generate_func_p関数だけです。

分割数の作成

def pn_list_func(n, k):
if n < k:
return []
if k==1:
return [[n]]
array = []
for elm in pn_list_func(n-1, k-1):
array.append(elm+[1])
for elm in pn_list_func(n-k, k):
array.append([item+1 for item in elm])
return array
def pn_aster_list_func(n, k):
array = []
for elm in pn_list_func(n+k, k):
new_elm = []
for item in elm:
if item > 1:
new_elm.append(item-1)
array.append(new_elm)
return array
def partition_generate_func_p(n):
return pn_aster_list_func(n, n)
partition_generate_func_p(6)

[[6],
 [5, 1],
 [4, 2],
 [3, 3],
 [4, 1, 1],
 [3, 2, 1],
 [2, 2, 2],
 [3, 1, 1, 1],
 [2, 2, 1, 1],
 [2, 1, 1, 1, 1],
 [1, 1, 1, 1, 1, 1]]

24.pn_aster_list_func関数に、引数n=n,k=nにより呼び出すだけです。

こうしてみると、いずれの方法でも分割を生成することができますが、この目的ではqnの方がより簡単に処理できるように思われます。

qnを使って整数分割を生成する

以前作成したqn_list_func関数を使って、整数分割を生成します。

qnから分割数を作成

def qn_list_func(n, k):
if n < k:
return []
if k==1:
return [[1] * n]
array = []
for elm in qn_list_func(n-1, k-1):
array.append([elm[0] + 1] + elm[1:])
for elm in qn_list_func(n-k, k):
array.append([k] + elm)
return array
def qn_aster_list_func(n, k):
array = []
for elm in qn_list_func(n+k, k):
array.append(elm[1:])
return array
def partition_generate_func_q(n):
return qn_aster_list_func(n, n)
partition_generate_func_q(6)

[[1, 1, 1, 1, 1, 1],
 [2, 1, 1, 1, 1],
 [2, 2, 1, 1],
 [2, 2, 2],
 [3, 1, 1, 1],
 [3, 2, 1],
 [3, 3],
 [4, 1, 1],
 [4, 2],
 [5, 1],
 [6]]

24.pn_aster_list_func関数に、引数n=n,k=nにより呼び出すだけです。

partition_generate_func_q関数と同じ結果ですが、出力される順番が逆になります。このように分割数には興味が尽きません。

分割数を写像から考える

不定方程式を使い分割数を生成する

分割数の考え方

分割数の考え方

不定方程式によるリストの作成

分割数の難しさ

K=3以外の場合も計算

不定方程式の結果をわかりやすく集計

増加写像を応用して分割数を降順にする

SymPyライブラリによる分割数の表示

分割数を計算する関数

分割を生成する関数

n=1から決められた数までの分割数を連続して生成する関数

分割を生成する関数の考え方

分割数を生成するプログラム

補助関数の導入

補助関数の意味と種類

補助関数の考え方

補助関数の漸化式

漸化式を使って分割を生成する

最大の和因子がKである補助関数を作成する

もう一つの補助関数

補助関数qkの漸化式

個数による分類と最大値による分類の1対1対応

ぴったりではなく、それ以下という補助関数

分割数がk以下である分割の数 p*(n,k)

最大の和因子がk以下の分割の個数 q*(n,k)

漸化式を応用して分割数を計算する

分割数の計算

漸化式を使った分割の生成

p(n,k)関数の応用

qnを使って整数分割を生成する

分割数がk以下である分割の数　p*(n,k)

最大の和因子がk以下の分割の個数　q*(n,k)