分割数を写像から考える

補助関数の導入

補助関数の意味と種類

補助関数の考え方

p(n)のように直接計算するのが難しい時には、計算しやすくするための補助関数(auxiliary function)という別の関数を使う手があります。

補助関数の1つの例としてp(n)を和因子の個数kで分類し、p(n ,k)とする方法があります。補助関数p(n, k)で個数を計算したのち、本丸のp(n)を落としに行く作戦です。例えばn=6、k=3の場合、(4, 1, 1)、(3, 2, 1)、(2, 2, 2)の3つの分割があります。SymPyライブラリのsympy.functions.combinatorial.numbersモジュールで提供されるnT関数を使用することにより分割を生成することができます。

Code 4.1　SymPyライブラリのnT関数で分割数の補助関数を計算する

from sympy.functions.combinatorial.numbers import nT
sym_nt_count = nT(6, 3)
print(type(sym_nt_count))
print(f'partition={int(sym_nt_count):>3}')


partition=  3

1.　nT関数の戻り値はpartition関数と同様にsympy.core.numbers.Integerクラスという特別な形式の整数の型になります。このため、3．で出力する場合にはint関数を適用します。

補助関数の大体の感覚をつかむため、nT関数を使いn=10、k=10までの一覧表を作成します。配列arrayに分割数を代入し、print_table関数を使い出力するのであらかじめ実行しておく必要があります。print_table関数はnに対するkごとの計算結果をsigmaとして列の右端に表示する機能があり、この値が分割数になっています。

Code 4.2　nT関数を使い、補助関数の一覧表を作成する

max_n = 10
max_k = 10
array = [[0] * (max_k + 1) for _ in range(max_n + 1)]
title = 'Triangular Table of Partition Numbers n＼k'
print(title.center(90))
print('')
for i in range(1, max_n + 1):
for j in range(1, max_k + 1):
array[i][j] = int(nT(i, j))
print_table(array, 3)

5.　タイトルを90文字に中央揃えして出力します。必要に応じパソコンの画面に合わせて調整してください。

この表を見ると、次のことがうかがえます。

n<kのようなnより分割数の方が大きいことは考えられないので0
k=1のときはnが大きくても、nが1つの分割にしか分けられないので1
n=kの場合はn個の1が和因子になる分割が1つしか考えられないので1

さらに表を眺めながら補助関数p(n, k)の具体的な構成を検討していきます。

補助関数の漸化式

p(n, k)を直接求めるのは難しいので、漸化式を考えます。例えば、p(9, 3)の分割数は図の通り7になります。このうち最小（最右端）の要素が1かどうかで、2つの集合、集合$X_1$、集合$X_2$に分類します。

集合$X_1$ 9の分割で和因子数3 最小和因子が1

集合$X_2$ 9の分割で和因子数3最小和因子が1以外

8の分割で和因子数2、つまりp(8, 2)の分割を集合Yとし、集合$X_1$との対応を考えます。集合$X_1$の最小和因子（右端）にある1を削除すると合計と和因子数が1ずつ減るので、集合Yに対応します。一方、集合Yの右端に1を追加すると、合計と和因子数が1ずつ減るので$X_1$に対応します。つまり、両者は逆写像を持ち、全単射（一対一対応）になります。一般化すると、P(n, k)のうち最小和因子が1=p(n-1, k-1)となります。

次に6の分割で和因子数3、つまりp(6, 3)の分割を集合Zとし、集合$X_2$との対応を考えます。集合$X_2$の3つの和因子からそれぞれ1ずつを差し引くと、最小和因子（右端）が2以上なので和因子数は3のままで、合計は引いて6になるので集合Zと対応します。一方、集合Zの3つの和因子に1ずつを加えると、和因子数は3のままで合計は9になり$X_2$に対応します。つまり、両者は逆写像を持ち、全単射（一対一対応）になります。一般化するとP(n, k)のうち最小和因子が2以上=p(n-k, k)となります。

まとめる次のような漸化式になります。

Equation 4.1　補助関数(p,k)を使った分割式の漸化式

n<kのとき0

k=1 またはn=kのとき　1

$p (n, k)= p(n-1, k-1) + p(n-k, k)$

さっそく漸化式を使い補助関数の個数を求めるプログラムを作成します。漸化式を再帰関数に落とし込むだけです。

Code 4.3　漸化式を使って補助関数の分割数を計算する

def calc_partition_aux(n, k):
if n < k:
return 0
if k == 1 or n == k:
return 1
return calc_partition_aux(n-1, k - 1) + calc_partition_aux(n - k, k)
calc_partition_aux(6, 3)

6.　n=6、k=3を引数として実行すると、n=5、k=2としてさらに関数calc_partition_auxを呼び出して、優先して実行します。さらにn=4,k=1としてさらに同じ関数が実行されます。

5.　n=4,k=1として関数calc_partition_auxを呼び出すと1を返します。この流れを繰り返すと最終的に分割数3が返り値となります。

こんな簡単なプログラムでp(n, k)を計算することができます。

補助関数の分割は、以前分割を生成するために使用したSymPyライブラリのsympy.utilities.iterablesモジュールで提供されるordered_partitions関数にkの引数を追加することにより生成することができます。

SymPyライブラリのordered_partition関数による補助関数による分割の生成

Code 4.4　SymPyライブラリのordered_partition関数を使い補助関数の分割を生成

from sympy.utilities.iterables import ordered_partitions
sym_ordered_partitions_93_list = []
for p in ordered_partitions(9, 3, sort = True):
sym_ordered_partitions_93_list.append(p[::-1])
sym_ordered_partitions_93_list

[[7, 1, 1], [6, 2, 1], [5, 3, 1], [4, 4, 1], [5, 2, 2], [4, 3, 2], [3, 3, 3]]

4.　p[::-1]とすることでリストpの順序を逆転させます。

漸化式を使って分割を生成する

さらに、次の漸化式を用いるとp(n, k)の一覧を生成することも可能です。こちらもp(n - 1, k - 1) 、p(n-k, k)を同じ関数で生成、これに漸化式の処理を加えるようにしています。

Code 4.5　漸化式を使って補助関数の分割数を生成する

def generate_partition_aux_pn(n, k):
if n < k:
return []
if k == 1:
return [[n]]
partition_list = []
for elm in generate_partition_aux_pn(n - 1, k - 1):
partition_list.append(elm + [1])
for elm in generate_partition_aux_pn(n - k, k):
partition_list.append([item + 1 for item in elm])
return partition_list
pn_aux_93_list = generate_partition_aux_pn(9, 3)
for i,j in zip(sym_ordered_partitions_93_list ,pn_aux_93_list):
print(f'{str(i):<14}{str(j):<14}')

7.　p(n-1, k-1)の戻り値を１つ1つelmに代入し、右側に1を付け足すことで①の処理ができます。

9.　p(n-k, k) の戻り値を１つ1つelmに代入し、elmの各要素に1を加える処理をしています。

一見すると、なぜ、こんなプログラムで分割を生成することができるのか不思議な感じがしますが、よくプログラムを見ると補助関数による漸化式を素直に反映してくれています。

最大和因子がKである補助関数を作成する

もう一つの補助関数

補助関数には別の視点で捉えるものとして組み合わせの最大値で分類する方法があり、ここではq(n, k)とします。

n<kのようなnより最大和因子の方が大きいことは考えられないので0
k=1のときはk個の和因子全ての和因子が1の分割が1つしか考えられないので1
n=kの場合は和因子がkのみの分割が1つしか考えられないので1

q(9 , 3)は和因子の最大値が3で左端に来るもので、図の通り7個あります。これも、前と同じように分けて考えます。

集合$X_1$ 9の分割で最大和因子が3、 2番目に大きな和因子（左から2番目）が3より小さい

集合$X_2$ 9の分割で最大和因子が3、 2番目に大きな和因子（左から2番目）も3

8の分割で最大和因子2、つまりq(8, 2)の分割を集合Yとし、集合$X_1$と対応させます。集合$X_1$の左端にある最大和因子から1を差し引いて2にしても2番目が2以下なので分割として扱うことができ、対応付けることができます。集合Yの左端に1を加えると$X_1$に対応するので、両者は逆写像を持ち、全単射（一対一対応）になります。

6の分割で最大和因が3、つまりq(6, 3)の分割を集合Zとし、集合$X_2$と対応させます。集合$X_2$の左端の和因子を削除しても2番目も３なので、最大和因子は3のままで集合Zと対応します。一方、集合Zの左端に最大和因子として3を付け加えると$X_2$に対応するので、両者は逆写像を持ち、全単射（一対一対応）になります。

①2番目に大きな和因子（左から2番目）が1番目より小さな分割　

②2番目に大きな和因子（左から2番目）が1番目と同じ分割

①は左端の和因子から1を差し引きます。結果として左端の和因子が2番目の和因子より小さくなることはないのでq(8, 2)と1対1の対応になります。逆にq(8,2)の左端に1を加えると①になり、全単射（1対1の対応）になります。

一方②は左端から1を引いても2番目が3なので降順であるという分割のルールに違反します。そこで、左端の最大値の3の和因子を削除します。②は2番目の和因子も１番目と同じなので、合計は6となり、最大和因子が3のまま6の分割になりq(6, 3)と全単射（1対1対応）になります。

上記の関係から、次の漸化式を導くことができます。

Equation 4.2　補助関数qkの漸化式

n<kのとき0

k=1 またはn=kのとき　1

$q (n, k)= q(n-1, k-1)+q(n-k, k) $

補助関数qkの漸化式

これはp(n, k)と全く同じ漸化式になります。個数を求めるだけであればpartition_r関数と同じになるのでそのまま流用できます。次に、分割数の生成も再帰関数を使うことができます。

Code 4.6　漸化式を使って補助関数の分割数を生成する

def generate_partition_aux_qn(n, k):
if n < k:
return []
if k==1:
return [[1] * n]
partition_list = []
for elm in generate_partition_aux_qn(n - 1, k - 1):
partition_list.append([elm[0] + 1] + elm[1:])
for elm in generate_partition_aux_qn(n - k, k):
partition_list.append([k] + elm)
return partition_list
qn_aux_93_list = generate_partition_aux_qn(9, 3)
qn_aux_93_list

[[3, 1, 1, 1, 1, 1, 1],
 [3, 2, 1, 1, 1, 1],
 [3, 2, 2, 1, 1],
 [3, 2, 2, 2],
 [3, 3, 1, 1, 1],
 [3, 3, 2, 1],
 [3, 3, 3]]

7.　漸化式の左側の部分$q(k-1, n-1) $を組み込んでいます。ここでは一番左側の和因子に1を足すことでq(k,n)の分割を生成しています。同じqn_list_func(n-1, k-1)を引数と変えて呼び出す再帰関数になっています。

9.　漸化式の右側の部分$q(n-k, k)$を組み込んでいます。ここでは、全ての分割の一番左側にkを追加することで、q(k,n)の分割を生成しています。

個数による分類と最大値による分類の1対1対応

前項の漸化式を見るとp(n, k)とq(n, k)の個数が等しいことがわかりましたが、その理由を考えます。

例えばp(6,3)、つまり合計6、和因子数3の1つの例として(4, 2, 1)を取り上げます。この分割に対して、図のよう点線を軸に反転させるとq(6,3)つまり、合計は6のままで最大値が3となる(3, 2, 1, 1)の分割になります。さらに、(3, 2, 1, 1)をもう一度反転させると(4, 2, 1)に戻ります。つまり1対1の対応になります。結局p(n, k)とq(n, k)は同じものを見る方向を変えただけということになります。このような関係を共役な分割(partition conjugate）といいます。

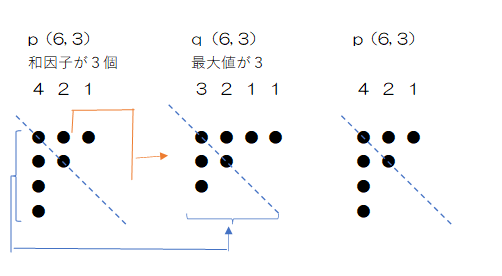
要素数が3の組み合わせ(4,2,1)を最大値が3の組み合わせ(3,2,1,1)に変換する関数を作成します。関数名は共役の英語表記からconjugate_funcとし、引数として分割をリストで渡します。戻り値として共役の分割がリストで返ります。ここでは(4,2,1)を例にして考えます。

Code 4.7　共役の分割に変換する関数

def generate_conjugate_partition (elm):
conjugate_elm = [0] * elm[0]
for item in elm:
for i in range(item):
conjugate_elm[i] += 1
return conjugate_elm
pn=[4, 2, 1]
print(generate_conjugate_partition (pn))
qn=[3, 2, 1, 1]
print(generate_conjugate_partition (qn))

[3, 2, 1, 1]
[4, 2, 1]

2.　最大和因子は引数elmの0番目の値（例の場合は4）なので、はじめにその長さのリストを定義し、全て0で初期化します。

3.　 elmの要素を1つ1つ読み込み、その値の個数だけconjugate_elmの値をカウントアップします。例えば、値が4であればインデックスが0から3の4つ、次の2であれば、0から1までの2つの項目に1を足します。

このことにより、最大値が4のリストを生成することができます。また、この逆の変換をすると元に戻ります。同じ関数を使いp(n,k)とq(n,k)を相互に変換させることができます。このような対応を対合写像（たいごう、ついごうinvolution）といいます。

ここで#12で生成したp(n)の分割にconjugate関数を適用した結果と、#13で生成したq(n)を比較します。

Code 4.8　generate_conjugate_partition関数を使い、p(n,k)=q(n,k)を確認する

conjugate_p = []
for elm in pn_aux_93_list:
conjugate_p.append(generate_conjugate_partition(elm))
if qn_aux_93_list == conjugate_p:
print('qn_aux_93_list == conjugate of pn_aux_93_list')
conjugate_q = []
for elm in qn_aux_93_list:
conjugate_q.append( generate_conjugate_partition(elm))
if pn_aux_93_list == conjugate_q:
print('pn_aux_93_list == conjugate of qn_aux_93_list')

qn_aux_93_list == conjugate of pn_aux_93_list
pn_aux_93_list == conjugate of qn_aux_93_list

2.　#で生成したp(9, 3)の分割に対して3.でgenerate_conjugate_partition関数を使い共役の分割に変換します。

9.　#で生成したq(9, 3)の分割に対して同様の処理をします。

2次元リストの比較は、単純に比較する場合、内側の要素がすべて正しくても並び順が異なると==演算子で比べた場合等しくなりません。この場合にはsorted関数で並べ替えないと正しい計算結果は得られません。ところが# 7で作成したgenerate_conjugate_partition関数ではソートをしなくても等しいとの結果になりました。漸化式を使いpnとqnを生成すると並び順も含めてしっかりと対応してくれます。このことからp(n,k)=q(n,k)であることを確認することができました。

n=1から決められた数までの分割数を連続して生成する関数

分割を生成する関数の考え方

前節では不定方程式を利用して分割を生成しましたが、ここでは直接に生成するプログラムを作成します。このとき、分割数の左端の最大和因子に注目する全単射を見出すことにより、面白いプログラムを作ることができます。

Code 4.9　和因子の最大値を順次挿入することにより分割数を計算

def generate_accumulated_partition_pn(n):
partition_list = [[()]]
for current_n in range(1, n+1):
new_partition = []
for i in range (current_n):
for elm in partition_list [i]:
if elm == () or elm[0] <= current_n - i:
new_partition.append((current_n - i,) + elm)
partition_list.append(new_partition)
return partition_list
generate_accumulated_partition_pn(6)

[[()],
 [(1,)],
 [(2,), (1, 1)],
 [(3,), (2, 1), (1, 1, 1)],
 [(4,), (3, 1), (2, 2), (2, 1, 1), (1, 1, 1, 1)],
 [(5,), (4, 1), (3, 2), (3, 1, 1), (2, 2, 1), (2, 1, 1, 1), (1, 1, 1, 1, 1)],
 [(6,),
  (5, 1),
  (4, 2),
  (4, 1, 1),
  (3, 3),
  (3, 2, 1),
  (3, 1, 1, 1),
  (2, 2, 2),
  (2, 2, 1, 1),
  (2, 1, 1, 1, 1),
  (1, 1, 1, 1, 1, 1)]]

2.　n=0の場合は空集合として定義します。

3.　以下で、nまで順次、分割数を求めます。

4.　作成中の分割数はnew_partition に積み上げていきます。

5.　作成中の分割より小さい分割をelmに代入し、順次チェックします。

6.　iの分割の中で集合Ｙに当てはまるものについて、k= current_n - iをnew_partitionに追加します。

7.　elm == ()という条件は、n=1を作成するときelmがブランクであるためです。or条件の左側がTrueになるとorの右側は評価されません。このためelm[0]はエラーになりません。

例えば、partition_func(6)を呼び出すと、数字6をさまざまな整数の和に分割したパターンがリストとして返されます。

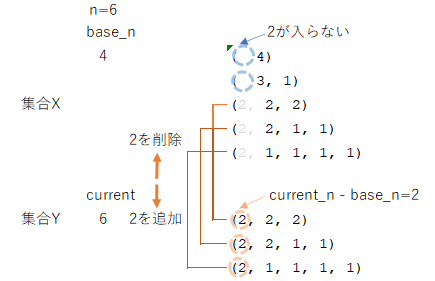
6の分割数11個を集合Xとします。これに対し、集合Xの分割の最も大きな数字（左端）を削除した分割を集合Yとします。例えば、集合Xの分割(2, 2, 1, 1)は、集合Yの(2, 1, 1)に対応します。(2, 1, 1)は4の分割になるので集合Yは6-2=4の分割数となります。このため、4の分割は全て集合Yの部分集合になるような気もしますが、実はそうではありません。例えば、(3,1)は4の分割数の1つですが、左端に2を追加すると降順であるという前提が崩れてしまいます。

少し面倒ですが、集合Ｙを別の視点から見ると、6以下のiに対して6-iの分割でなおかつ最大和因子がiであるものと定義することができます。ここで、集合Yから集合Xへの対応を考えます。(2, 1, 1)は4の分割なので6との差2を左に追加しても降順であるとの分割を満たすので集合Xの(2, 2, 1, 1)に対応付けられ写像であるといえます。

このことから集合Xと集合Yは全単射（一対一対応）といえます。

分割数を生成するプログラム

この考え方から分割数を生成するプログラムを作成します。最終的な6の分割数は[(6),(5,1)・・・]のようにリストのなかに分割数がタプルとして埋め込まれるようにしますが、全単射の考え方を取り入れるため、1から５までの分割数を順次計算し、その結果を積み上げていくので3次元の配列になります。

関数名はpartition_func(n)とし、引数は求めたい分割のnとします。今計算している分割をcurrent_n、参照している分割をiとして定義するので、削除、追加をするk= current_n - iとなります。

P(9,3)を求めるためには、p(8,2)の分割に対し、和因子1を追加します。

Code 4.10　和因子の最大値を順次挿入することにより分割数を計算

def generate_accumulated_partition_qn(n):
partition_list = [[()]]
for current_n in range(1, n + 1):
new_partition=[]
for elm in partition_list[-1]:
new_partition.append(elm + (1,))
for i in range (1, current_n):
for elm in partition_list[i]:
if len(elm) == current_n - i:
new_partition.append(tuple([x+1 for x in elm]))
partition_list.append(new_partition)
return partition_list
generate_accumulated_partition_qn(6)

 [[()],
 [(1,)],
 [(1, 1), (2,)],
 [(1, 1, 1), (2, 1), (3,)],
 [(1, 1, 1, 1), (2, 1, 1), (3, 1), (2, 2), (4,)],
 [(1, 1, 1, 1, 1), (2, 1, 1, 1), (3, 1, 1), (2, 2, 1), (4, 1), (3, 2), (5,)],
 [(1, 1, 1, 1, 1, 1),
  (2, 1, 1, 1, 1),
  (3, 1, 1, 1),
  (2, 2, 1, 1),
  (4, 1, 1),
  (3, 2, 1),
  (5, 1),
  (2, 2, 2),
  (4, 2),
  (3, 3),
  (6,)]]

分割をこんな簡単なプログラムで生成することができるのは驚きです。しかし、処理の中身を見るとnの分割数を求めるのに、毎回1からn-1までの分割数を1つ１つ見に行くので計算効率は低いため、分割数 p(n) のみ求める場合は漸化式等を使うほうが効率的です