和因子数、補助関数を使い分割を生成する

最大和因子数で制限を掛ける補助関数

和因子数がk以下である分割の数　p*(n,k)

最大和因子数で制限を加えた補助関数

これまで、nの分割で和因子数がkのp(n,k)についてみてきました。これに対して和因子数がk個以下とする関数をp*(n, k)と定義します。

例えばp*(6, 3)は次の3つに分類されます。

①p(6, 3) (4, 1, 1), (3, 2, 1), (2, 2, 2)

②p(6, 2) (5, 1),(4, 2),(3, 3)

③p(6, 1) (6)

p*(6, 3)を求めるためには、①から③を関数により合計すればよいわけですが、それではあまりに芸がありません。そこで、p*(n, k) を生成するため、p(n+k, k)つまりp(9,3)との関係を調べます。

P(9, 3)を次のとおり分類します。

①和因子に1が含まれていない分割　 (5, 2, 2),(4, 3, 2),(3, 3, 3)

②和因子に1が1つ含まれている分割 (6, 2, 1),(5, 3, 1),(4, 4, 1)

③和因子に1が2つ含まれている分割 (7, 1, 1)

①の代表として(3, 3, 3)を取り上げます。各和因子を1つずつ差し引くとp(6, 3)の(2, 2, 2)に対応します。(5, 2, 2),(4, 3, 2)についても同様です。

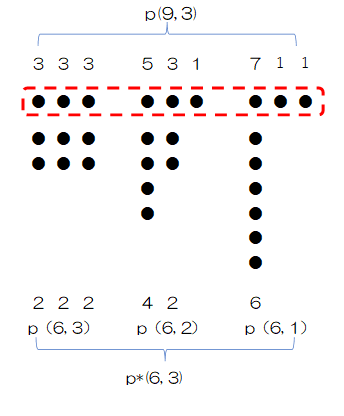
Figure 4.1　p(n,k)とp*(n,k)との全単射（一対一対応）
p(n,k)とp*(n,k)との全単射（一対一対応）

②の代表として(5, 3, 1) を取り上げます。各和因子を1つずつ差し引くと (4, 2, 0)になり、右側の0を削除するとp(6, 2)の(4, 2)になります。

③の要素(7, 1, 1) を取り上げます。各和因子を1つずつ差し引くと (7, 0, 0)になり、右側の0、2つを削除するとp(6, 1)の(6)になります。

逆に、p*(6, 3)の要素に対し、和因子数が1,2の場合は右側に0を補い、和因子数3の分割し、それぞれ１ずつ加えると(9, 3)になります。

結果的にp*(6, 3)とp(9, 3)はお互いに逆写像を持つ一対一対応となります。

Equation 4.1　p(n, k)とp*(n, k)の個数を比較する比較

p(n+k, k) = p*(n, k)

補助関数の漸化式を確認

さっそくp*(6,3)とp(9,3)の関係を確かめます。generate_partition_pn関数を使い、p(9,3)を生成し、ここから各和因子を1ずつ差し引きます。次にP*(6,3)はp(6,1),p(6,2),p(6,3)を結合してリストpn_63に代入し、p(9,3)も同じ関数で生成してp_93に代入し、分割ごとに比較します。

Code 4.17　p(n+k, k)とp*(n,k)の関係

  1. pn_93_list = generate_partition_pn(9, 3)
  2. pn93_decremented_list=[]
  3. for pn_93 in pn_93_list:
  4. pn93_decremented_list.append([item -1 for item in pn_93 if item >1])
  5. pn_accumed_63_list = []
  6. for i in range(1, 4):
  7. pn_accumed_63_list += generate_partition_pn(6, i)
  8. print(f' pn(9,3) decremented accumed_pn(6,3)')
  9. print(f'----------------------------')
  10. for pn_93, pn93_decremented, pn_accumed_63 in zip(pn_93_list, pn93_decremented_list, pn_accumed_63_list):
  11. print(f'{str(pn_93):<14}{str(pn93_decremented):<12}{str(pn_accumed_63):<12}')
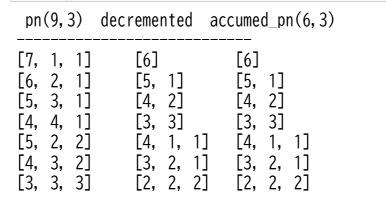
    補助関数pnと最大値pnの比較

7.　pn_93とpn_aster_63をzip関数で要素ごとに組み合わせて出力します。

8.　2つのリストを並べて見やすくするため、列幅を14文字分とします。str関数でリストを文字列に変換すると列幅を指定することができます。

p(n)とp*(n)の関係が分かったところで、generate_partition_pn関数の引数nをn+kにして呼び出すことにより、p*(n)を生成する関数を作成します。ここから、k個の和因子から1を引き、０になったら削除するよう処理をします。

SymPyライブラリのpartitions関数で補助関数による分割を生成

SymPyライブラリのpartitions関数で補助関数で比較

先ほどご紹介したp(n)を生成するpartitions関数は、2番目の引数を指定するとp*(n, k)を生成に絞り込むことができます。

Code 4.18　SymPyライブラリのpartitions関数を使い、最大和因子数を指定して分割を生成

  1. from sympy.utilities.iterables import partitions
  2. sym_partitions_63_dict = list(partitions(6, 3))
  3. sym_partitions_63_list = []
  4. for partition_dict in sym_partitions_63_dict:
  5. sym_partitions_63_list.append(dict_convert_to_list(partition_dict))
  6. print(f' decremented sym_pn(6,3) ')
  7. print(f'----------------------------------')
  8. for sym_partitions_63, pn93_decremented in zip(
  9. sym_partitions_63_list, pn93_decremented_list
  10. ):
  11. print(f'{str(sym_partitions_63):<16}{str(pn93_decremented):<12}')
partitions関数と最大値pnの比較

2.　 partitions関数を使うことにより、p(6, 3)を辞書形式で生成し、sym_partitions_63_dictに代入します。

4.　2で生成した辞書形式の分割を1つ1つ読み込み、dict_convert_to_listを使いリストに変換してsym_partitions_63_listに代入します。

このように、partitions関数を使うとp*(n, k)、つまり、最大和因子数kのnの分割を生成することができます。ordered_partitionsが和因子数k（最大でない）の分割であるのと比較すると比較すると興味深いものがあります。

関数の作成

ここでp*(n, k)を生成する関数を作成します。

Code 4.19　pn*を使って分割を生成

  1. def generate_partition_pn_lt(n, k=None):
  2. if k is None:
  3. k = n
  4. n += k
  5. partition_list = []
  6. for elm in generate_partition_pn(n, k):
  7. partition_list.append([x-1 for x in elm if x > 1])
  8. return partition_list
  10. print('p(6, 3)')
  11. print(generate_partition_pn_lt(6, 3))
  12. print('p*(6, 3)')
  13. print(generate_partition_pn_lt(6))
p(6, 3)
[[6], [5, 1], [4, 2], [3, 3], [4, 1, 1], [3, 2, 1], [2, 2, 2]]
p*(6, 3)
[[6], [5, 1], [4, 2], [3, 3], [4, 1, 1], [3, 2, 1], [2, 2, 2], [3, 1, 1, 1], [2, 2, 1, 1], [2, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1]]

2.　k引数 k が省略された場合、デフォルトとしてn を設定します。同時に調整フラグ lt を True にします。

4.　調整フラグ lt が True の場合、整数 n に k を加算します。

7.　整数分割を生成するために、関数 generate_partition_pn(n, k) を呼び出します。調整フラグ lt が True の場合、各分割要素から1を減じた後、1を超える値だけを残して、新しい分割リストを作成します。調整を行わない場合は、得られた分割をそのまま利用します。

このプログラムは、整数 n の分割（指定された整数を複数の整数の和で表す方法）を生成する関数です。オプションとして、分割する整数の数の上限を示す引数 k、および分割方法を調整するかどうかを示すフラグ lt を指定できます。lt が True の場合、整数 n に k を加えた数の分割を求め、その後に各分割から最初の要素を取り除きます。これにより、整数 n を k 個以下の整数に分割した結果を得ることができます。

最大和因子がk以下の分割の個数　q*(n,k)

最大和因子がk以下の分割q*(n ,k)を生成します。

最大の和因子で制限を加えた補助関数

最大和因子数で制限を加えた補助関数

例えばは次の3つに分類されます。

①q(6, 3)　 (3, 1, 1, 1) (3, 2, 1)(3, 3)

②q(6,2) (2, 1, 1, 1, 1)(2, 2, 1, 1)

③q(6,1) (1, 1, 1, 1, 1, 1)

q*(n,k) とq(n+k,k)の関係を具体的な例をもとに考えるため、q*(6,3)とq(9,3)の関係を調べます。

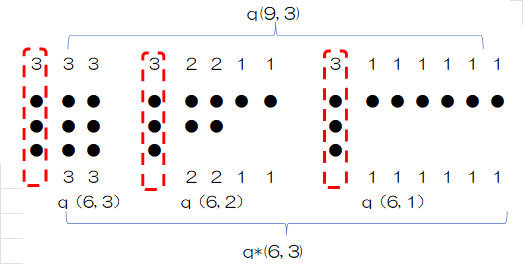
q(9,3)を次のとおり分類します。

①2番目に大きな和因子が3の分割　(3, 3, 1, 1, 1) (3, 3, 2, 1)(3, 3, 3)

②2番目に大きな和因子が2の分割 (3, 2, 1, 1, 1, 1)(3, 2, 2, 1, 1)

③2番目に大きな和因子が1の分割 (3, 1, 1, 1, 1, 1, 1)

①の代表として(3,3,3)を取り上げます。最大和因子（左端）の3を削除するとq(6,3)の(3,3)に対応します。(3, 1, 1, 1),( 3, 2, 1)についても同様です。

②の代表として(3, 2, 2, 1, 1) を取り上げます。最大和因子（左端）の3を削除すると 、q(3,2 ) の(2, 2, 1, 1)になります。

③の要素(3, 1, 1, 1, 1, 1, 1) を取り上げます。最大和因子（左端）の3を削除すると 、q(3,1 ) の(1, 1, 1, 1, 1, 1)になります。

逆に、q*(6,3)の要素に対し、最大和因子（左端）に3を追加するとq(9,3)になります。

結果的にq*(6, 3)とq(9, 3)はお互いに逆写像を持ち一対一対応となります。

Figure 4.2　q(n,k)とq*(n,k)
q(n,k)とq*(n,k)

補助関数の漸化式を確認

generate_partition_qn関数を使い生成したq(9,3)のリストqn_93_listから、先頭の要素を削除したリストとqn93_without_first_listと、q*(6,3)としてq(6,1),q(6,2),q(6,3)を結合したリストqn_accumed_63_listを比較し、両者が一致していることを確認します。

Code 4.20　q(n+k, k)とq*(n,k)の関数を比較

  1. qn_93_list = generate_partition_qn(9, 3)
  2. qn93_without_first_list =[elm[1:] for elm in qn_93_list]
  3. qn_accumed_63_list = []
  4. for i in range(1, 4):
  5. qn_accumed_63_list += generate_partition_qn(6, i)
  7. print(f' pn(9,3) without_first accumed_pn(6,3)')
  8. print(f'-----------------------------------------------------------------------')
  9. for qn_93, qn93_without_first, qn_accumed_63 in zip(qn_93_list, qn93_without_first_list, qn_accumed_63_list):
  10. print(f'{str(qn_93):<26}{str(qn93_without_first):<26}{str(qn_accumed_63):<26}') 
qnとqn最大値の比較

2.　リスト内容表記で、各分割の先頭の要素をスライスします。Code 4.17で生成したp*よりも簡単な操作で変換することができます。

このことからp(n)とp*(n)の関係が明らかになりました。

SymPyライブラリのpartitions関数で補助関数による分割を生成

SymPyライブラリのpartitions関数で補助関数を生成

SymPyライブラリなど既存のライブラリには、q*nの分割を生成する関数は見当たりません。そこで、partitions関数でp*nの分割を生成したリストにgenerate_conjugate_partition関数を適用しq*nに変換します。

Code 4.21　SymPyのpartitions関数の共役で比較する

  1. sym_partitions_63_conjugate_list = []
  2. for elm in sym_partitions_63_list:
  3. sym_partitions_63_conjugate_list.append(generate_conjugate_partition(elm))
  4. sym_partitions_63_conjugate_list
  5. print(f'without_first conjugate_sym_qn(6,3) ')
  6. print(f'-----------------------------------------------')
  7. for qn93_without_first, sym_partitions_63 in zip(
  8. qn93_without_first_list, sym_partitions_63_conjugate_list
  9. ):
  10. print(f'{str(qn93_without_first):<22}{str(sym_partitions_63):<16}')
 partitions関数と最大値qnの比較

3.　 generate_partition_qn(n+k, k)で生成したリストに対し、最大和因子（左端）を削除してarrayに追加します。qn_93の方が、分割の左端を削除するだけなので処理が簡単なのがわかります。

共役変換したものとはいえ、SymPy関数と一致することがわかりました。

qn*による分割の生成

SymPy関数のお墨付きを得たため、generate_partition_qn関数を活用し、q*nを生成する関数を作成します。nの分割を生成するためにはq(n, n)とすれば足りますが、kに初期値nとすることで、kを省略した場合は分割を生成するようにします。

Code 4.22　qn*を使って分割を生成

  1. def generate_partition_qn_lt(n, k=None):
  2. if k is None:
  3. k = n
  4. partition_list = []
  5. for elm in generate_partition_qn(n+k, k):
  6. partition_list.append(elm[1:])
  7. return partition_list
  9. print('q(6, 3)')
  10. print(generate_partition_qn_lt(6, 3))
  11. print('p*(6, 3)')
  12. print(generate_partition_qn_lt(6))
q(6, 3)
[[1, 1, 1, 1, 1, 1], [2, 1, 1, 1, 1], [2, 2, 1, 1], [2, 2, 2], [3, 1, 1, 1], [3, 2, 1], [3, 3]]
p*(6, 3)
[[1, 1, 1, 1, 1, 1], [2, 1, 1, 1, 1], [2, 2, 1, 1], [2, 2, 2], [3, 1, 1, 1], [3, 2, 1], [3, 3], [4, 1, 1], [4, 2], [5, 1], [6]]

2.　引数 k が指定されない場合、初期値として k は n に設定されます。

3.　generate_partition_qn 関数を呼び出して、整数n+K

4.　n+k を k 以下の整数で分割します。各分割から先頭要素を取り除いた新しい分割をリストに追加します。

分割数を計算する関数

最後に、分割数を計算する関数を作成します。この関数では補助関数の個数を計算するcalc_partition_nk関数を使い、kを指定したら補助関数を、さらにlt=Trueとするとに設定すると、最大許容和因子数 k 以下での分割数を計算します。さらにkを省略したらnの分割を生成します。

漸化式を使った分割数を計算する関数をまとめます。この関数では、引数にnのみを指定した場合は分割数、(n,k)を指定した場合は補助関数、aster=Trueとしたときはk個以下の合計を計算することとします。

この関数は、整数の分割数を効率的に計算するための汎用的な再帰関数です。3つの異なるモードで動作し、オプション引数により計算対象を切り替えることができます：

通常モード（k指定）：合計nを和因子数k個で分割する場合の数 p(n, k) を計算

アスタリスクモード（aster=True）：合計nを最大和因子k以下で分割する場合の数 q(n,k) を全分割モード（k=None）：整数nの全分割数 p(n) を計算します。

Code 4.23　漸化式を使って分割数の個数を計算する

  1. def calc_partition(n, k=None, lt=False):
  2. if lt:
  3. n += k
  4. elif k is None:
  5. k = n
  6. n = 2 * n
  7. return calc_partition_nk(n, k)
  9. print('p(6, 3) = ',calc_partition(6, 3))
  10. print('p*(6, 3) =' ,calc_partition(6, 3, lt=True))
  11. accumed = 0
  12. for i in range(1, n+1):
  13. accumed += calc_partition(6, i)
  14. print('p(6, 1) + p(6, 2) + p(6, 3) = ', accumed)
  15. print('p6=',calc_partition(6))
  16. print('p*(6, 6) = ',calc_partition(6, 6, lt=True))
p(6, 3) =  3
p*(6, 3) = 7
p(6, 1) + p(6, 2) + p(6, 3) =  11
p6= 11
p*(6, 6) =  11

2.　内部的には数学的な漸化式を使い、nにkを加え最大和因子数を求めるようにします。

4.　kが省略したときはnの分割数を計算するためkにnをnを2nとします。

7.　2.4のように引数を調整して、分割の補助関数の個数を計算するcalc_partition_nk関数を呼びだします。

ictsr4 All Rights Reserved.