再帰関数を使い分割を生成する

漸化式を応用して分割を計算する

前節ではpn（和因子数がk）、qn（最大和因子がk）による漸化式をpn_lt（和因子数がk以下）、qn_lt（最大和因子がk以下）に拡張する方法で分割を生成してきました。この章では、pn_lt、qn_ltを直接求める漸化式による再帰関数を作成し、分割を生成します。ただし、一足飛びに再帰関数を作成するのは難しいので、考え方を理解するための分割を1からn-1まで順次累積し、nの分割の生成においては、これまで累積した分割を活用していくプログラムを作成します。

pnの漸化式を使った分割を1からnまで累積して生成

整数nを、要素数が最大k個となるような整数分割を累積的に生成する関数です。各整数1からnまでを順番に処理し、それぞれの整数分割を前の結果を再利用しながら構築します。リストpartition_listに1からnまでの分割を生成し、結果を格納します。また、現在処理をしているnをcurrent_nとします。

[[()],
 [(1,)],
 [(2,), (1, 1)],
 [(3,), (2, 1), (1, 1, 1)],
 [(4,), (3, 1), (2, 2), (2, 1, 1)],
 [(5,), (4, 1), (3, 2), (3, 1, 1), (2, 2, 1)],
 [(6,), (5, 1), (4, 2), (4, 1, 1), (3, 3), (3, 2, 1), (2, 2, 2)]]

2.　 0の分割は空集合なので空タプル () とし、これを含むリストを partition_list に格納して初期化します。

3.　1 から n までの各整数 current_n について、分割を構成していきます。

4.　current_partition は、現在の整数 current_n の分割を一時的に格納するリストとして初期化します。

5.　 辞書順降順にするため分割の先頭の数 head を大きい順に降順で試します。

6.　残りの数 remaining = current_n - head を求め、既存の分割と組み合わせる準備をします。

7.　remaining に対してすでに構築されている分割（再利用）を tail として取り出します。

8.　条件分岐：tail が空の場合（最初の構成）、または head ≥ tail[0]（降順を保つ）かつ len(tail) ≤ k-1（長さ制限）を満たす場合に、(head,) + tail を新しい分割として current_partition に追加します。

current_nの分割を生成する際に、current_n -1までに作成した分割を巧みに使い分割を累積していきます。次にこの考え方を使い、分割を生成する再帰関数に発展させていきます。

pn_ltを使って整数分割を生成する

generate_partition_with_max_length関数とします。

(6,)
(5, 1)
(4, 2)
(4, 1, 1)
(3, 3)
(3, 2, 1)
(3, 1, 2)
(2, 4)
(2, 3, 1)
(2, 2, 2)
(2, 1, 3)
(1, 5)
(1, 4, 1)
(1, 3, 2)
(1, 2, 3)
(1, 1, 4)

1.　k の値が指定されていない場合、自動的にk=n と設定し、最大で𝑛までの整数を使用可能とします。

4.　残りの数が 0 になったときは、これ以上分割ができない（分割が完成した）ことを示します。このとき () （空のタプル）を yield して再帰処理を終了します。

7.　現在使用可能な最大整数を min(k, n) とし、そこから 1 までの範囲を降順で順に試します。こうすることで、和の要素が必ず head 以下になるよう制限します。

8.　一度選択した整数 head を先頭として固定し、残りの数n-headを新たに分割します。ただし、次に使用可能な最大和因子は head とします。結果的に非増加列であることを保ちます。

9.　再帰呼び出しから返された部分分割 tail の前に head を付加した分割を逐次生成します。

partition_generate_func_qn関数と同じ結果ですが、出力される順番が逆になります。このように分割数には興味が尽きません。

qnにより分割を生成する

累積するプログラムを作成

pnと同様に、累積するプログラムを作成します。

2次元リストの比較は、単純に比較する場合、内側の和因子がすべて正しくても並び順が異なると==演算子で比べた場合等しくなりません。この場合にはsorted関数で並べ替えないと正しい計算結果は得られません。ところがgenerate_conjugate_partition関数ではソートをしなくても等しいとの結果になりました。漸化式を使いpnとqnを生成すると並び順も含めてしっかりと対応してくれます。このことからp(n,k)=q(n,k)であることを確認することができました。

例えば、partition_func(6)を呼び出すと、数字6をさまざまな整数の和に分割したパターンがリストとして返されます。

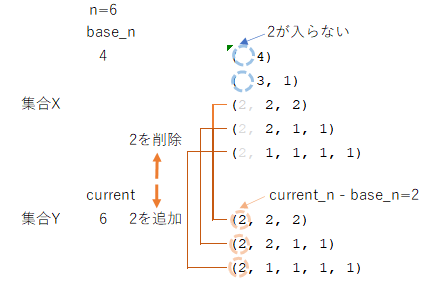
6の分割数11個を集合Xとします。これに対し、集合Xの分割の最も大きな数字（左端）を削除した分割を集合Yとします。例えば、集合Xの分割(2, 2, 1, 1)は、集合Yの(2, 1, 1)に対応します。(2, 1, 1)は4の分割になるので集合Yは6-2=4の分割数となります。このため、4の分割は全て集合Yの部分集合になるような気もしますが、実はそうではありません。例えば、(3,1)は4の分割数の1つですが、左端に2を追加すると降順であるという前提が崩れてしまいます。

少し面倒ですが、集合Ｙを別の視点から見ると、6以下のiに対して6-iの分割でなおかつ最大和因子がiであるものと定義することができます。ここで、集合Yから集合Xへの対応を考えます。(2, 1, 1)は4の分割なので6との差2を左に追加しても降順であるとの分割を満たすので集合Xの(2, 2, 1, 1)に対応付けられ写像であるといえます。

このことから集合Xと集合Yは全単射（一対一対応）といえます。

([[()],
 [(1,)],
 [(2,), (1, 1)],
 [(3,), (2, 1), (1, 1, 1)],
 [(3, 1), (2, 2), (2, 1, 1), (1, 1, 1, 1)],
 [(3, 2), (3, 1, 1), (2, 2, 1), (2, 1, 1, 1), (1, 1, 1, 1, 1)],
 [(3, 3),
  (3, 2, 1),
  (3, 1, 1, 1),
  (2, 2, 2),
  (2, 2, 1, 1),
  (2, 1, 1, 1, 1),
  (1, 1, 1, 1, 1, 1)]]

2.　 partition_list[0] に、長さ 0 の分割（空タプル）のみを格納します。これは動的計画における初期条件となります。

3.　1 から n まで順に分割を作成していきます。最終的に partition_list[n] が整数 n に対応する分割リストとなります。

3.　今回の current_n に対する分割を一時的に格納するためのリストを初期化します。

4.　分割の先頭要素（最大値）として使用できる整数を、current_n と k のうち小さい方を上限として 降順 に試します。これにより、先頭要素が k を超えないよう制限します。先頭要素 head を選んだあとの「残りの値」を計算します。

6.　すでに構築済みの partition_list[remaining] から、残りの値 remaining を分割したリスト（タプル）を順に取り出していきます。これを利用することで、動的計画法ならではの効率的な列挙が可能になります。

7.　分割の要素が大きい順あるいは非増加列となるよう条件を課しています。具体的には、tail が空タプルなら（=まだ要素がない場合）、どんな head でも先頭として使える。すでに先頭要素を持つ tail であれば、tail[0] <= head を満たすことにより、先頭要素が等しいかそれより小さい値に制限します。

8.　要件を満たした分割 tail に先頭要素 head を付加して、新たな分割タプルを current_partition に追加します。

9.　今回の current_n に対して構築できたすべての分割リストを partition_list に追加し、次の current_n + 1 の計算に備えます。

0 から n までの各 current_n に対応する分割リストをすべてまとめた partition_list を返します。

最大要素がk以下という制限つきで、整数 𝑛のすべての分割を構築します。

分割を効率的に集約するために動的計画法を活用しており、計算途中で生じるサブ問題（remaining の分割）を再利用する点が特徴となっています。

分割を生成するプログラムの決定版

整数nの分割（ある整数を複数の整数の和で表現する方法）を効率的に生成するためのジェネレータ関数です。オプショナルな引数として「最大和因子 」（分割に使用可能な最大整数）を指定することができ、省略した場合は自動的に となり、すべての整数を使用して分割を生成します。

その際、常に残りの数から、これまでに選択された整数の和を引いた値を意識しながら、順に分割候補を生成していきます。

(3, 3)
(3, 2, 1)
(3, 1, 1, 1)
(2, 2, 2)
(2, 2, 1, 1)
(2, 1, 1, 1, 1)
(1, 1, 1, 1, 1, 1)
(6,)
(5, 1)
(4, 2)
(4, 1, 1)
(3, 3)
(3, 2, 1)
(3, 1, 1, 1)
(2, 2, 2)
(2, 2, 1, 1)
(2, 1, 1, 1, 1)
(1, 1, 1, 1, 1, 1)

2.　 最大和因子k が指定されていない場合、 自体を最大値として設定します。これにより、1から n までのすべての整数を使用可能とします。

4.　 分割を繰り返していき、残りの数が 0 になった時点で、1つの分割が完成したことを示します。この時、空のタプル () を返して再帰処理を終了します。

7.　 現時点で利用可能な最大の整数から順に（降順で）和因子として試していきます。最大和因子kを 、残りの数をnと比較し、小さい方を上限として整数 を選択します。

8.　 整数iを選択した後、残りの数はn-iになります。これを新しいnとして再帰的に関数を呼び出し、さらに分割を進めます。この時、次に選べる最大整数は現在のiを超えないように制限します。

9.　 再帰呼び出しで得られた分割（prev）に、現在選んだ整数 i を追加して新しい分割タプルを作り、それを yield によって順次返します。

すべての i について再帰と結合を繰り返すことで、条件を満たすすべての整数分割が網羅的に yield されます。このように、generate_partition はジェネレータなので、すべての分割を一度にメモリに載せる必要がありません。n が大きい場合でも、1つずつ取り出しながら処理したいときに便利です。

以上のように、generate_partition_qn_accumulated(n, k) は、動的計画法を使った効率的な分割列挙を行う仕組みです。利用者は、この返り値のうち partition_list[n] を取り出すことで、目的の分割集合を簡単に参照できます。

generate_partition(6, 6)

├─ i=6 → generate_partition(0, 6) → ()

│ → (6,)

├─ i=5 → generate_partition(1, 5)

│ └─ i=1 → generate_partition(0, 1) → ()

│ → (5, 1)

├─ i=4 → generate_partition(2, 4)

│ ├─ i=2 → generate_partition(0, 2) → ()

│ │ → (4, 2)

│ └─ i=1 → generate_partition(1, 1)

│ └─ i=1 → generate_partition(0, 1) → ()

│ → (4, 1, 1)

i=2: generate_partition(4, 2)

|

+-- n=4, k=2 → min(4,2)=2 → for i=2,1

|

+-- i=2 → generate_partition(2,2)

|

+-- n=2, k=2 → min(2,2)=2 → for i=2,1

+-- i=2 → generate_partition(0,2) # (2,2)

+-- i=1 → generate_partition(1,1)

+-- i=1 → generate_partition(0,1) # (2,1,1)

+-- i=1 → generate_partition(3,1)

+-- i=1 → generate_partition(2,1)

+-- i=1 → generate_partition(1,1)

+-- i=1 → generate_partition(0,1) # (1,1,1,1)