Pythonによるベクトルの和の計算
ベクトルの定義と和の計算
Pythonでベクトルの計算をするときは、NumPyやSymPyモジュールを使うのが一般的ですが、計算の考え方を知るためリストによる表現からはじめます
リストによるベクトルの定義と計算
ベクトルの定義と和の計算
要素2つの2次元のベクトルを配列として定義します。通常は$\vec{a}$=($a_1$,$a_2$)、$\vec{b}$=($b_1$,$b_2$)のようにあらわし、小さな文字1,2を添え字といいます。
vectorの定義
- a = [4, 1]
- b = [2, 3]
ベクトルの和を求めます。このときには、ベクトルの同じ添え字の要素同士を足し合わせます。
ベクトルの和
- v_add = [4+2,1+3]
- v_add
[6, 4]
ベクトルの和を図形にすると、次のようにイメージできます。

ベクトルの差の計算
ベクトルの差を計算します。ここでは$\vec{b}$-$\vec{a}$の計算をしています。
ベクトルの差
- v_dif = [2-4,3-1]
- v_dif
[-2, 2]
ベクトルの差を図形にすると、次のようにイメージできます。

リストによる定義と計算
次に成分が3つの三次元のベクトルの計算をします。ここでは、2つのベクトルv_a=(1, 2, 3)、v_b=(4, 5, 6)をリストとして定義し、これらの和を計算します。
ベクトルの定義
- v_a = [1, 2, 3]
- v_b = [4, 5, 6]
カウンタを使ってfor文で回す方法
最も単純な方法を使ってリストv_add1でベクトルの和を計算します。
リストによるベクトルの和 ~ forループによる方法
- v_add1 = []
- for i in range(len(v_a)):
- v_add1.append(v_a[i]+v_b[i])
- v_add1
[5, 7, 9]
要素同士の和を計算するためのベクトルv_add1を空のリストとして定義ます。for文で各要素の添え字ごとに取り出し、和を計算した結果をappendメソッドでリストに追加します。うまく計算することができたものの、v_aの長さ(次元数)を使いfor文を回すのはあまりスマートとはいえません。
zip関数を使ってforループを回す方法
次に、zip関数を使って2つのリストから同時に要素を取り出す方法で計算します。
ベクトルの和 ~ PythonらしくZipを使う方法
- v_add2 = []
- for elm_a, elm_b in zip(v_a, v_b):
- v_add2.append(elm_a + elm_b)
- v_add2
結果は、同じです。少しPythonらしく計算することができました。
リスト内包表記による方法
さらにPythonらしい計算方法である、リスト内包表記によりベクトルの和を計算します。
リスト内包表記によるベクトルの和
- v_add3 = [elm_a + elm_b for elm_a, elm_b in zip(v_a, v_b)]
- v_add3
1行で計算できるのでとても便利ですが、リスト内包表記は2つのリストを扱うとわかりにくくなるのが難点です。
lambda式による方法
lambda式でも計算することができます。
lambda式によるベクトルの和
- v_add4 = list(map(lambda elm_a, elm_b: elm_a + elm_b, v_a, v_b))
- v_add4
結果はいずれも同じです。通常のリストを使う方法によるとPythonのプログラミングの練習にはなりますが、単純なベクトルの和の計算だけでも手間がかかります。
NumPyによる定義と計算
NumPyモジュールを使うと簡単にベクトルの計算をすることができます。NumPyの配列にはndarrayとmatrixの2つの形式があり、表記の仕方が異なります。
ndarrayによるベクトルの和の計算
まず、一般的なndarrayからです。ndarray はN-dimensional array の略で、N次元配列という意味合いがあります。
NumPyのインポートと、ndarrayによるベクトルの和の計算
- import numpy as np
- na_a = np.array([1, 2, 3])
- na_b = np.array([4, 5, 6])
- na_add = na_a + na_b
- na_add
array([5, 7, 9])
NumPyにはベクトル演算という機能があり、同じサイズの配列の算術演算においては、同位要素(同じ場所の要素)ごとに計算されます。単純に足し算をするだけなのでとても簡単です。
matrixによるベクトルの和の計算
次に、matrixによる方法です。
NumPyのmatrixによるベクトルの定義
- nm_a = np.matrix('1 2 3')
- nm_b = np.matrix('4 5 6')
- nm_add = nm_a + nm_b
- nm_add
matrix([[5, 7, 9]])
1. ベクトルの定義はnp.matrix([1 2 3])としても問題ありませんが、matrix形式に限り上記の通り書くことができます。ndarray形式の場合には固定長の文字列(u7)になってしまいます。
4. 結果はmatrix形式で返ります。
NumPyは数値計算用のモジュールでベクトル計算も簡単になりますが、これだけならExcelの方が手っ取り早いように思われます。Pythonのすごさはここから先になります。
SymPyによる定義と計算
SymPyモジュールはPython library for symbolic mathematicsの略で、代数を扱うことができます。SymPy では、Matrixとしてベクトルを扱います。
SymPyによるベクトルの定義と和の計算
はじめにベクトルを定義して和を計算します。
SymPyのインポートと、Matrixによるベクトルの定義と和の計算
- import sympy
- sn_a = sympy.Matrix([1, 2, 3])
- sn_b = sympy.Matrix([4, 5, 6])
- sn_add = sn_a + sn_b
- sn_add
結果は次の通り縦のベクトルで表示されます。
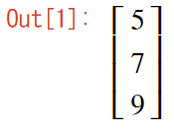
SymPy のMatrixとしてベクトルを定義して和を計算します。結果は、縦のベクトルで表示されます。
SymPyによるベクトルの代数計算
単純なベクトルの和ではNumPyと何ら変わりはありませんが、SymPyのすごさは代数計算をすることができることです。
代数としてベクトルを定義する
SymPyの代数計算によるベクトルの和の計算
- sympy.var('a_x,a_y,a_z,b_x,b_y,b_z')
- sa_a = sympy.Matrix([a_x, a_y, a_z])
- sa_b = sympy.Matrix([b_x, b_y, b_z])
- sa_add = sa_a + sa_b
- sa_add
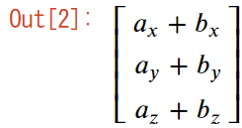
Pythonは変数を明示的に定義しなくてもよい仕様になっていますが、SymPyでは、1行目のようにsympy.varでa_x,a_y,a_z,b_x,b_y,b_zとして定義しておく必要があります。次に、2つのベクトルの和をsa_addに変数として格納しています。
subsメソッドにより代数で定義したベクトルに数値を代入する
代数として定義したベクトルに対しsubsメソッドを使い、具体的な数値を代入します。
SymPyの代数に辞書形式で数値を代入
- sa_add.subs({a_x: 1, a_y: 2, a_z: 3, b_x: 4, b_y: 5, b_z: 6})
次に変数が格納されているベクトルに辞書形式を使ってsubsメソッドで数値をしてすると、前例のように計算することができます。結果は#8と同じように縦のベクトルで表示されます。
SymPyの代数計算によるベクトルの和の計算
- sa_add.subs([(a_x, 1), (a_y, 2), (a_z, 3), (b_x, 4), (b_y, 5), (b_z, 6)])
このほか、代数と数値を表すタプルをリストとして数値をあてはめることもできます。
ベクトルをグラフで表現する
Pythonでグラフを使いベクトルを表現するため、ndarray形式でベクトルを定義し、matplotlibを使いイメージをグラフにします。
ベクトルの和の計算
ベクトルの和を図解する
- import numpy as np
- import matplotlib.pyplot as plt
- o = np.array([0, 0])
- v_x = np.array([4, 1])
- v_y = np.array([2, 3])
- vector = [(o, v_x, 'b'), (o, v_y, 'g' ), (o, v_x+v_y, 'r'),(v_x,v_y, (0.0,1.0, 0.0,0.4)),(v_y,v_x, (0.0,0.0, 1.0,0.4))]
- fig ,ax= plt.subplots(figsize=(6,6))
- for tail, head, color in vector:
- ax.quiver(*tail,*head,
- color=color, units='xy', scale=1,linestyles='dashed', linewidth=1)
- ax.set_title('vector sum', fontsize=20)
- ax.set_xlabel('x') # x軸ラベル
- ax.set_ylabel('y') # y軸ラベル
- ax.set_xlim(0, 6.5)
- ax.set_ylim(0, 6.5)
- plt.show()

ベクトルの差の計算
ベクトルの差も同じように描くことができます。
ベクトルの差を図解する
- vector = [(o, v_x, 'b'), (o, v_y, 'g' ), (v_x, v_y-v_x, 'r')]
- fig ,ax= plt.subplots(figsize=(6,6))
- for tail, head, color in vector:
- ax.quiver(*tail,*head,
- color=color, units='xy', scale=1,linestyles='dashed', linewidth=1)
- ax.set_title('Vector difference', fontsize=20)
- ax.set_xlabel('x') # x軸ラベル
- ax.set_ylabel('y') # y軸ラベル
- ax.set_xlim(0, 4.5)
- ax.set_ylim(0, 4.5)
- plt.show()

このように簡単にベクトルを描くことができます。