Pythonでの小数点の扱いと四捨五入
Pythonでの割り算で割り切れない場合の表示される桁数
通常のPytonでの割り算
Pythonで割り切れない割り算をすると次のようになります。
#1 Pythonによる割り算 print(1 / 6) print(1 / 7) print(1 / 17) print(1 / 81) print(1 / 113) print(1 / 9801)
0.16666666666666666 0.14285714285714285 0.058823529411764705 0.012345679012345678 0.008849557522123894 0.00010203040506070809
1 / 6 の計算のように、6が無限に循環する数値については小数点以下第17位まで表示し、それ以降は四捨五入をせず切り捨てられてしまいます。1/17のようにさらに分母を大きくすると、小数点第1位が0になるので小数点第18位まで表示されます。要は頭の0を抜かした小数部分の表示(有効桁数)が17桁になります。通常の計算であれば、ここまでの精度は要求されることはありません。
decimalモジュールを使った割り算
これに対し、1/7の商を見ると142857が無限にしていますが、これを循環小数といいます。この循環小数について調べようとすると、もっと有効桁数を多くしたくなります。
このときに便利なのがdecimalモジュールです。decimalモジュールを使うと次のようになります。
#3 decimalモジュールを使った割り算
from decimal import *
print(Decimal('1') / Decimal('6'))
print(Decimal('1') / Decimal('7'))
print(Decimal('1') / Decimal('17'))
print(Decimal('1') / Decimal('81'))
print(Decimal('1') / Decimal('113'))
print(Decimal('1') / Decimal('9801'))
0.1666666666666666666666666667 0.1428571428571428571428571429 0.05882352941176470588235294118 0.01234567901234567901234567901 0.008849557522123893805309734513 0.0001020304050607080910111213142
#4 decimalモジュールを使った割り算(有効桁数100桁)
from decimal import *
getcontext().prec = 100
print(Decimal('1') / Decimal('6'))
print(Decimal('1') / Decimal('7'))
print(Decimal('1') / Decimal('17'))
print(Decimal('1') / Decimal('81'))
print(Decimal('1') / Decimal('113'))
print(Decimal('1') / Decimal('9801'))
0.1666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666667 0.1428571428571428571428571428571428571428571428571428571428571428571428571428571428571428571428571429 0.05882352941176470588235294117647058823529411764705882352941176470588235294117647058823529411764705882 0.01234567901234567901234567901234567901234567901234567901234567901234567901234567901234567901234567901 0.008849557522123893805309734513274336283185840707964601769911504424778761061946902654867256637168141593 0.0001020304050607080910111213141516171819202122232425262728293031323334353637383940414243444546474849505
decimalモジュールで有効桁数を変更する
このように、decimalモジュールの有効桁数は28桁がデフォルトなので、先ほどよりは桁数は増えます。1/Xが循環小数だとすると、循環する桁数はXより小さくなるはずです。なぜなら図の通り学校で習った割り算をすると、枠で囲った部分の数字が前と同じものが出現した場合、次からは同じ計算の繰り返しになるためです。
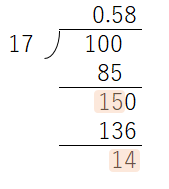
ですから1/7くらいなら良いのですが、1/17になると28桁の表示ではいささか怪しくなります。このようなことは、小数点以下100桁程度の計算ができないと見つけることができません。このときには、getcontext オブジェクトのprec属性(getcontext().prec)を100桁に指定します。これで商の循環の仕方がよく分かります。
循環小数の計算
ここからは余談ですが循環小数というのは奥深いものがあります。
例えば1/81は1234567890の10桁がきれいに循環します。
もっとすごいのは1/113です。これも最大の112桁”8849557522123893805309734513274336283185840707964601769911504424778761061946902654867256637168141592920353982300”で循環します。こうなるとgetcontext().precを300位に設定しないと分かりません。ちなみに355/113は円周率πにとても近い値になります。
#5 113を分母にしてた割り算
from decimal import *
import math
getcontext().prec = 300
print(Decimal('1') / Decimal('113'))
getcontext().prec = 10
print(Decimal('355') / Decimal('113'))
print(Decimal(math.pi))
0.00884955752212389380530973451327433628318584070796460176991150442477876106194690265486725663716814159292035398230088495575221238938053097345132743362831858407079646017699115044247787610619469026548672566371681415929203539823008849557522123893805309734513274336283185840707964601769911504424778761061947 3.141592920 3.141592653589793115997963468544185161590576171875
循環小数の計算
恐るべき循環小数1/9801
最後にもっとすごいのは1/ 9801です。循環する桁数は198とそんなにすごいわけではありませんが、循環の仕方に驚きます。
エクセルとの比較
#5 decimalモジュールを使った割り算(1/9801有効桁数300桁)
from decimal import *
getcontext().prec = 300
print(Decimal('1') / Decimal('9801')
0.000102030405060708091011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969799000102030405060708091011121314151617181920212223242526272829303132333435363738394041424344454647484950515
このあたりエクセルだと有効桁数が17桁程度なので歯が立ちません。実務でどこまで使うかは分かりませんが、いろいろ調べてみると興味は尽きません。