Pythonによるベクトルの内積と外積の計算

ベクトルの定義と内積の計算

リストによる定義と計算

Pythonでベクトルの内積や外積の計算をする方法をご紹介します。ベクトルの計算はNumPyやSymPyモジュールを使うが一般的ですが、まずは、計算の流れを知るためリストによる計算からはじめます。ここでは、2つのベクトルv_a=(2, -1, 2)、v_b=(3, -2, 1)を定義して、2つのベクトルの内積を求めます。

1. #1 ベクトルの内積の計算
2. v_a = [2, -1, 2]
3. v_b = [3, -2, 1]
4. v_c = 0
5. for x, y in zip(v_a,v_b):
6. v_c += x * y
7. v_c

10

内積は、ベクトルの中で同じサイズの配列の算術演算では、同位要素（同じ場所の要素）ごとの積の合計することで計算します。式は次の通りです。

はじめに合計を計算するための変数v_ｃを0として定義し、for文の中で対応する要素の積をzip関数で1つずつ取り出して積を求め変数v_ｃに加算していきます。

NumPyによる内積の計算

Numpyのndarrayの積を求めることで計算

NumPyにより内積を計算します。

1. #2 Numpyのインポートと、ndarrayによるベクトルの定義
2. import numpy as np
3. n_a = np.array([2, -1, 2])
4. n_b = np.array([3, -2, 1])
5. print('arrayの積：', n_a * n_b)
6. print('内積：', sum(n_a * n_b))

arrayの積： [6 2 2]
内積： 10

NumPyでは、n_aとn_bの積を計算すると同じ位置の要素の積の配列になります。内積はその合計なので、このsum関数でその配列の合計を求めます。

関数などにより内積を計算

さらに、内積を計算する演算子、関数やメソッドを使うと、もっと簡単に内積を計算することができます。

1. #3 Numpyの関数などによる内積の計算
2. print('@演算子による内積：',n_a @ n_b)
3. print('dot関数による内積：',np.dot(n_a, n_b))
4. print('dot関数はリストでも可：',np.dot(v_a, v_b))
5. print('inner関数による内積：',np.inner(n_a, n_b))
6. print('inner関数はリストでも可：',np.inner(v_a, v_b))
7. print('dotメソッドによる内積：',n_a.dot(n_b))

@演算子による内積： 10
dot関数による内積： 10
dot関数はリストでも可： 10
inner関数による内積： 10
inner関数はリストでも可： 10
dotメソッドによる内積： 10

1. 2行目の”@”という記号（演算子）は内積を意味します。
2. 3行目はdot関数によりndarrayで表現したベクトルの内積を計算することができます。ちなみに、内積を別の言い方ではdot積（dot product）といいます。
3. 4行目のように、dot関数は、通常のPythonのリストでも内積を計算することができます。
4. 5行目のようにinnner関数でも内積（innner product）を計算することができます。innner関数も、6行目のようにリストでも内積を計算することができます。
5. 7行目のように、1つのベクトルにもう一つのベクトルをdotメソッドを適用することで内積を計算することができます。

SymPyによる内積の計算

SympyのMatricesの内積の計算

SymPyでは1列のMatricesとしてベクトルを定義し、dotメソッドで計算します。NumPyのnp.dot(n_a, n_b)のような関数を使うことはできません。

1. #4 SymPyでの数値による内積の計算
2. import sympy
3. s_a, s_b = sympy.symbols('s_a s_b')
4. s_a = sympy.Matrix([2, -1, 2])
5. s_b = sympy.Matrix([3, -2, 1])
6. s_a.dot(s_b)

結果は同様に10となります。

SymPyの代数を使った内積の計算

SymPyでは、ベクトルの代数計算できます。ここでは、ベクトルの内積を代数で求めます。スカラーとして変数を定義した変数を使い1列のMatrixとしてベクトルを定義します。これに対し、dotメソッドにより代数として内積を計算することができます。

1. #5 sympyでの代数による内積の計算
2. sympy.var('a_x:z,b_x:z,c_x:z,d_x:z')
3. s_a = sympy.Matrix([a_x, a_y, a_z])
4. s_b = sympy.Matrix([b_x, b_y, b_z])
5. s_c = s_a.dot(s_b)
6. s_c

結果はs_cに格納され、その中身は次の通りです。

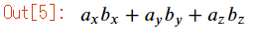
代位数で計算した内積s_Cにsubsメソッドで数値を代入します。数値の代入は、辞書形式によるのが一般的です。

1. #6 代数による内積の計算結果に数値を代入
2. s_c.subs({a_x: 2, a_y: -1, a_z: 2, b_x: 3, b_y: -2, b_z: 1})

また、タプルによる代入も可能です。

1. #7 代数による内積の計算結果に数値を代入
2. s_c.subs([(a_x, 2), (a_y, -1), (a_z, 2), (b_x, 3), (b_y, -2), (b_z, 1)])

結果は10になります。

Pythonによる外積の計算

Pythonを使って外積を計算します。

リストによる外積の計算

定義に従って、リストから計算することを考えます。外積は3次元のベクトルで計算します。

計算方法は次の通りです。

1. #8 リストによる外積の計算
2. v_a = [2, -1, 2]
3. v_b = [3, -2, 1]
4. v_aa = v_a + v_a[0:2]
5. v_bb = v_b + v_b[0:2]
6. v_o =[]
7. for i in range(len(v_a)):
8. v_o.append(v_aa[i+1]*v_bb[i+2]-v_aa[i+2]*v_bb[i+1])
9. v_o

[3, 4, -1]

1. 第2要素の計算には第3要素と第1要素を、第3要素の計算には第1要素と第2要素を使いfor文で計算するため、4行目、5行目でリストに第1要素と第2要素を追加します。
2. 7行目のfor文でリストの要素数（通常は3）までループさせます。
3. 2のループの中で、1つ下の要素と2つ下の要素をたすき掛けにして積を求めたのち、その差をと取ることでリストの各要素の値としてリストに挿入します。

結果は[3, 4, -1]となり、正しく計算することができました。

NumPyの関数による外積の計算

同じ位置の要素同士の計算であればNumPyのベクトル計算が有効ですが、外積については他の位置の要素を使うので、その方法は思いつきません。その代わりにNumPyには外積を計算する関数が用意されています。

ここでは、NumPyのndarrayによりベクトルを定義し、cross関数により外積を計算します。外積はクロス積（cross product）ともいいます。

1. #9 NumPyのcross関数による外積の計算
2. import numpy as np
3. n_a = np.array([2, -1, 2])
4. n_b = np.array([3, -2, 1])
5. np.cross(n_a,n_b)
6. np.cross(v_a,v_b)

前に定義した通常のリストを使っても同じ結果が返ります。

SymPyによる外積の計算

SymPyの1列のMatrixとしてベクトルを定義して外積を計算します。NumPyと異なり、1つのベクトルに対してもう1つのベクトルをメソッドとして適用すると、縦ベクトルとして表示されます。

1. #10 Sympyのcross methodによる外積の数値による計算
2. import sympy
3. s_a = sympy.Matrix([2, -1, 2])
4. s_b = sympy.Matrix([3, -2, 1])
5. s_a.cross(s_b)

次に、SymPyで代数としてベクトルを定義して外積を計算します。同じようにcrossメソッドを提供すると次のようになります。

1. #11 Sympyのcross methodによる外積の代数による計算
2. sympy.var('a_x:z,b_x:z,c_x:z,d_x:z')
3. sv_a =sympy.Matrix([a_x,a_y,a_z])
4. sv_b =sympy.Matrix([b_x,b_y,b_z])
5. sv_c=sv_a.cross(sv_b)
6. sv_c

いったんsv_cに結果を格納し表示すると次の通りになります。

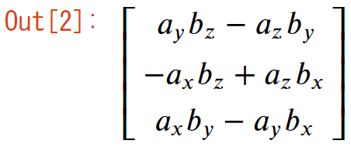
これに対して、subsメソッドで数値を代入します。

1. #12 SymPyのcross methodによる外積の計算
2. sv_c.subs({a_x:2,a_y:-1,a_z:2,b_x:3, b_y:-2, b_z:1})

前と同じ結果になります。

外積の次元に関する補足

外積は通常3次元のベクトルを想定していますが、NumPyでは2次元のベクトルにcross関数を使うことができます。

1. #13 2次元のベクトルに対する外積の計算
2. n2_a = np.array([1, 2])
3. n2_b = np.array([4, 5])

np.cross(n2_a,n2_b)結果はarray(-3)と、第1要素と第2用素をたすき掛けした積の差が計算されます。これに対して、4次元のベクトルで計算すると次のようなエラーとなります。

1. #14 4次元のベクトルに対する外積の計算
2. n4_a = np.array([1, 2, 3, 4])
3. n4_b = np.array([5, 6, 7, 8])
4. np.cross(n4_a,n4_b)

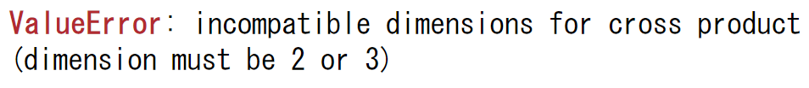
エラー表示からも、NumPyでは2次元か3次元を想定していることがわかります。

同じように、SymPyは3次元のみで、2次元以下や4次元以上のベクトルではエラーになります。