Pythonによるベクトルのノルムの計算

Pythonでベクトルのノルム（大きさ）を計算します。まず、計算の流れを知るためリストによる計算からはじめ、次にNumPyモジュールによる計算を考えます。ノルムの計算では最後に平方根を使うので、すっきり整数になることはむしろ稀です。この場合、SymPyモジュールを使うと、ルートによる表示も少数表示も可能となるので非常に扱いやすくなります。

ベクトルの定義とノルムの計算

リストによる定義と計算

forループによるノルムの計算

すっきりと整数となるケースとしてベクトルv_a=(2, 4, 4)のノルムから計算します。

  1. #1 ベクトルのノルムの計算
  2. import math
  3. v_a =[2, 4, 4]
  4. norm_a = 0
  5. for i in v_a:
  6. norm_a += i**2
  7. math.sqrt(norm_a)
    1. 平方根を計算するため、2行目でmathモジュールをインポートします。
    2. 5行目のforループで、ベクトルの各要素をiとして取り出します。
    3. 4行目で定義したnorm_aに対し、各要素の二乗を計算して足しこんでいきます。
    4. 計算式は$\sqrt{2^2+4^2+4^2}=\sqrt{36}$となり6ときれいに整数になります。

リスト内包表記によるノルムの計算

リスト内包表記によりベクトルのノルムを計算します。

  1. #2 リスト内包表記によるノルムの計算
  2. import math
  3. math.sqrt(sum([i**2 for i in v_a]))

lambda式によるノルムの計算

また、lambda式を使うと次の通りになります。

  1. #3 lambda式によるノルムの計算
  2. import math
  3. math.sqrt(sum(map(lambda i: i**2, v_a)))

いずれも、変数が1つなので簡単な式で表現することができます。

NumPyによるノルムの計算

Numpyで定義に従ってノルムを計算する

NumPyモジュールではベクトル演算を使うと、各要素を2乗してsum関数で合計することにより簡単に計算することができます。平方根の計算もNumPyモジュールに関数が用意されています。

  1. #4 NumPyによるノルムの計算
  2. import numpy as np
  3. n_a = np.array([2, 4, 4])
  4. np.sqrt(sum(n_a**2))

結果は同じく6となります。

NumPyのnorm関数によるノルムの計算

関数を使うと、簡単にノルムを計算することができます。NumPyにはlinalg （Linear algebra） という線形代数を扱うサブモジュールがあり、その中のnorm関数を使うことによりノルムを計算することができます。norm関数に求めたいベクトルを代入するだけで、計算は完了です。

  1. #5 Numpyのnorm関数によるノルムの計算
  2. np.linalg.norm(n_a)
  3. np.linalg.norm(n_a, ord=2)

通常はL2ノルムといい各要素の2乗の合計を2乗根することでノルムを計算しますが、L1ノルム（各要素の絶対値の合計）やL3ノルム（各要素を3乗して合計した値の3乗根）として計算する場合もあります。このため、ord=2というように、L2ノルムであることを明示する方がより確実になります。

結果はいずれも6になります。

SymPyによるノルムの計算

SymPyによるノルムの計算

SymPyモジュールでは1列のMatrixとしてベクトルを定義し、normメソッドで計算します。ordを省略するとL2ノルムで計算されますが、ここではあえてord=2と明示することにします。

  1. #6 Sympyのnorm関数によるノルムの計算
  2. import sympy
  3. s_a = sympy.Matrix([2,4,4])

s_a.norm(ord=2)結果は同様に6となります。SymPyモジュールを使うメリットは代数計算ができることです。

次のように変数を定義し、normメソッドを適用することで、ノルムの代数による計算結果を得ることができます。

  1. #7 SymPyでの代数によるノルムの計算
  2. import sympy
  3. sympy.var('a_x:z')
  4. s_a=sympy.Matrix([a_x,a_y,a_z])
  5. s_c=s_a.norm(ord=2)
  6. s_c

ここでは計算結果がs_cに格納され、次のように表示されます。

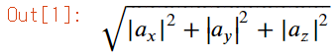
SymPyにノルムの代数計算
SymPyにノルムの代数計算

最後にs_cに、subsメソッドで数値を代入します

  1. #8 平方根をSympyにより計算した場合
  2. sn_n = s_c.subs({a_x:2,a_y:4,a_z:4})
  3. sn_n

結果はやはり6になります。

割り切れない場合のノルムの計算

これまではノルムがすっきりと整数になる例を取り扱ってきましたが、ベクトル[1, 4, 1]のように割り切れないケースを考えます。

NumPyにより割り切れない場合のノルムの計算

NumPyのndarrayで定義したベクトルに対しノルムを計算します。

$norm=\sqrt{1^2+4^2+1^2}=3\sqrt{2}$

  1. #9 平方根を計算した結果が割り切れない場合
  2. n_b = np.array([1, 4, 1])
  3. np.sqrt(sum(n_b**2))

4.242640687119285

小数点以下が延々と続くことになり扱いづらくなります。このような場合にSymPyが本領を発揮します。

NumPyの関数による外積の計算

SymPyで前と同じように計算します。

  1. #10 平方根を計算した結果が割り切れない場合
  2. import sympy
  3. s_b = sympy.Matrix([1,4,1])
  4. s_b.norm(ord=2)

$3\sqrt{2}$

今回はすっきりと割り切れませんが、ルート表示で結果を得ることができます。同様に、前に求めた代数による結果に数値を代入しても同様です。

  1. #11 平方根をSympyにより計算した場合
  2. sn_n = s_c.subs({a_x:1,a_y:4,a_z:1})
  3. sn_n

最後に、ルート表示した結果を小数点で表示する場合にはpythonのfloat関数を使うか、SymPyモジュールのN関数を使います。N関数では小数点以下の桁数を指定することができます。

  1. #12 Sympyで計算した結果を小数点表示に転換
  2. print('float関数による表示',float(sn_n))
  3. print('N関数で小数点第3位まで表示：',sympy.N(sn_n,4))

float関数による表示 4.242640687119285
N関数で小数点第3位まで表示： 4.243

float関数では#9のNumPyと同じ表示になります。N関数は2つ目の引数で四捨五入をする桁数を指定します。このケースでは小数点第4位を四捨五入し、小数点第3位まで表示されます。