Pythonの内積、外積、ノルムに関する計算
Pythonでベクトルの内積、外積、ノルム(大きさ)を計算してきましたが、これらの関連で興味深い計算をしてみます。
2つのベクトルのノルムと内積から角度を計算する
内積の定義とベクトルの成分の関係
ベクトルの内積は次の通り定義されます。
ベクトルの内積の定義
これに対し、内積とベクトルの成分の関係は次の通りです。
ベクトルの内積のベクトルの成分の関係
とすると、内積はベクトルの成分を使い次の通り表すことができます。
このことから、2つのベクトルの角度を計算することができます。
- import math
- a=[1,3]
- b=[2,1]
- dot_ab = sum([elm_a*elm_b for elm_a,elm_b in zip(a,b)])
- norm_a = math.sqrt(sum(elm_a**2 for elm_a in a))
- norm_b = math.sqrt(sum(elm_b**2 for elm_b in b))
- print(f'内積:{dot_ab:.6f} aのノルム:{norm_a:.6f} bのノルム:{norm_b:.6f}')
- cos_ab=dot_ab/(norm_a*norm_b)
- theta_ab = math.acos(cos_ab)
- pi_ab = theta_ab/math.pi
- degree_ab = math.degrees(theta_ab)
- print(f'cos:{cos_ab:.6f} 弧度法:{theta_ab:.6f}rad = {pi_ab:.2f}π 度数法:{degree_ab:.0f}度')
内積:5.000000 aのノルム:3.162278 bのノルム:2.236068 cos:0.707107 弧度法:0.785398rad = 0.25π 度数法:45度
2.3. リストとして2次元のベクトルを定義します。
4. 2つのベクトルの内積を計算します。ここではリスト内包表記を使います。
5.6. 2つのベクトルのノルムを計算します。
8. 内積、ノルムから2つのベクトルのなす角のcosの値を計算します。
9. mathモジュールのacos関数を使い、8.のarccosを計算します。つまり、角度$\theta$を計算します。この値は、弧度法(単位:radian)によります。
10. 弧度法は$\pi$を単位とするので、math.piで割ります。この結果$0.25\pi$となります。
11. thetaに対し、mathモジュールのdegrees関数を使うと、おなじみの度数法(度を単位)に変換することができます。
NumPyで2つのベクトルのなす角度を計算する
2つのベクトルn_aとn_bをndarrayで定義し、それぞれのノルムと内積を計算します。
一般にの関係にあるので、内積をノルムの積で割ることで2つのベクトルのなす角のcos(コサイン)を計算することができます。
NumPyによる2つのベクトルの角度の計算
- import numpy as np
- n_a = np.array([1, 4, 1])
- n_b = np.array([2, 5, 5])
- normn_a = np.sqrt(sum(n_a**2))
- normn_b = np.sqrt(sum(n_b**2))
- dotn_ab = np.dot(n_a, n_b)
- cosn_ab = dotn_ab/(normn_a*normn_b)
- "n_aのノルム:{:.6f} n_bのノルム:{:.6f} 内積:{:.6f} cos_ab:{:.6f}".format(
- normn_a, normn_b, dotn_ab, cosn_ab)
n_aのノルム:4.242641 n_bのノルム:7.348469 内積:27.000000 cos_ab:0.866025
それぞれ小数点第6位まで表示するようにしましたが、いまひとつすっきりとしません。
SymPyで2つのベクトルのなす角度を計算する
SymPyで2つのベクトルの内積からなす角のcosを求める
SymPyモジュールを使うと、次の通り平方根についてルート付きで表示することができます。その前提として、SymPyとともに、IpythonのMathモジュールをインポートしておきます。このことにより、数式をわかりやすく表示することができます。
SymPyによるベクトルの角度の計算
- import sympy
- from IPython.display import Math
- s_a, s_b = sympy.symbols('s_a s_b')
- s_a = sympy.Matrix([1, 4, 1])
- s_b = sympy.Matrix([2, 5, 5])
- norm_a = s_a.norm(ord=2)
- norm_b = s_b.norm(ord=2)
- dot_ab = s_a.dot(s_b)
- cos_ab= dot_ab/(norm_a*norm_b)
- display(Math(r'n_aのノルム=%s' sympy.latex(norm_a)))
- display(Math(r'n_bのノルム=%s' % sympy.latex(norm_b)))
- display(Math(r'内積=%s' % sympy.latex(dot_ab)))
- display(Math(r'cos=%s' % sympy.latex(cos_ab)))
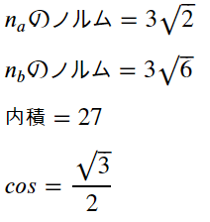
Matrixとしてベクトルを定義し、normメソッドでノルムを、dotメソッドで内積を計算して、内積を2つのノルムの積で割ることで、角度に対するcosの値をルート付きで表示することができます。このためIpython.displayのMath関数を使います。
SymPyでcosの値から角度を計算する
cosの値が求まったので、これを角度に変換するためarccos (アークコサイン) を計算します。このため、多くのコンピュータ言語と同様、SymPyでもarccosはacos関数を使って計算します。
cosの値から角度を計算(arccos)
- theta_ab=sympy.acos(cos_ab)
- display(Math(r'\theta=%s' % sympy.latex(theta_ab)))
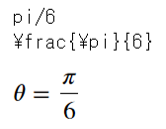
SymPyでは角度はラジアン(radian:弧度法)で表示されますが、どうしもピンとこないので、角度(degree:度数法)による表示に変換します。
ラジアン(radian:弧度法)から角度(degree:度数法)への変換
- import math
- deg=math.degrees(sympy.acos(cos_ab))
- deg
30.000000000000004
mathモジュールのdegrees関数を使うのが最も簡単です。結果は次の通り、ぴったりとはいきませんが、ベクトルs_aとs_bがなす角度は30度であることがわかりました。
2つのベクトルがなす平行四辺形と三角形の面積の計算
2つのベクトルがなす平行四辺形と三角形の面積にはいろいろな求め方があるので、これらを振り返りながらPythonを使って計算します。
2つの辺の長さとこれをはさむ角度がわかっている場合
2つの辺の長さとこれをはさむ角度がわかっている場合、次の式で面積を計算します。
という式になります。三角形の面積はこの1/2になります。
ここではすでに、aの辺の長さはnorm_a、bはnorm_b、2辺をなす角度はtheta_abで計算されているので、次のプログラムで計算することができます。
四辺形、三角形の面積
- rec_1 = norm_a * norm_b * sympy.sin(theta_ab)
- tri_1 = rec_1/2
- display(Math(r'四辺形の面積=%s' % sympy.latex(rec_1)))
- display(Math(r'三角形の面積=%s' % sympy.latex(tri_1)))
結果は、平行四辺形の面積はrec_1、三角形の面積はtri_1となります。Math関数を使うと次の通り表示されます。
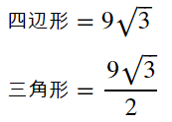
外積から計算する方法
2つのベクトルの各要素の値がわかっていれば、そこからなす平行四辺形の面積は、2つのベクトルの外積のノルムの値に一致します。ここではすでにs_aとs_bはsympy.matrixで定義されているので、ここから外積を求め、ノルムを取ることで平行四辺形と三角形の面積を計算します。
外積から平行四辺形と三角形の面積を計算する
- cross_ab=s_a.cross(s_b)
- rec_2 = cross_ab.norm(ord=2)
- tri_2 = rec_2 /2
- display(Math(r'外積=%s' % sympy.latex(cross_ab)))
- display(Math(r'四辺形の面積=%s' % sympy.latex(rec_2)))
- display(Math(r'三角形の面積=%s' % sympy.latex(tri_2)))
結果は次の通りです。高校数学では外積を取り扱っていないようですが、このように応用範囲が広いのでとても残念な気がします。

2つのベクトルの終点を結ぶ直線を使い面積を計算する
ベクトルs_aの終点を始点として、ベクトルs_bの終点を終点とするベクトルs_abを取ります。このベクトルのノルムが三角形の3つめの辺の長さになります。
2つのベクトルの終点を結ぶベクトルとそのノルム
- s_ab = s_b-s_a
- norm_ab=s_ab.norm(ord=2)
- display(Math(r'終点を結ぶベクトル=%s' % sympy.latex(s_ab)))
- display(Math(r'ベクトルのノルム=%s' % sympy.latex(norm_ab)))
ベクトルs_abとそのノルムは次の通りです。
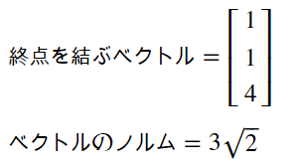
また、2つの辺の長さがnorm_a、norm_bで、2つのベクトルをはさむ角度がcos_abで計算されているので、余弦定理を使うことにより3つ目の辺の長さを計算することができます。
余弦定理による三角形の辺の計算
- sympy.sqrt(norm_a ** 2 + norm_b ** 2 -2*cos_ab*norm_a*norm_b)
答えは同じく\3\sqrt{2}\になります。
以上のことから、2つのベクトルとその終点を結ぶベクトルのノルムが求まりました。三角形の面積はヘロンの定理によって求めることができるので早速、計算してみます。
ヘロンの定理による三角形の面積の計算
- s=(norm_a+norm_b+norm_ab)/2
- tri_3=sympy.sqrt(s*(s-norm_a)*(s-norm_b)*(s-norm_ab))
- display(Math(r'三角形の面積=%s' % sympy.latex(tri_3)))
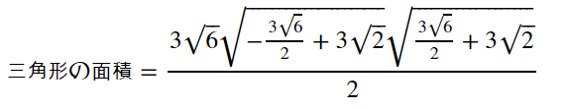
式が複雑になるので、計算結果も一見すると間違っているように見えます。この場合、SymPyではsimplify関数を使うと式を簡潔にすることができます。
複雑な式を簡潔にする
- display(Math(r'簡潔にした表示=%s' % sympy.latex(sympy.simplify(tri_3))))
このことにより、前と同じ結果になります。

正弦定理や内積を使って三角形の面積を計算する
最後に、少し変わった方法を使って三角形の面積を計算します。
正弦定理を使う方法
2ベクトルがなす角度と、終点を結ぶベクトルのノルム(長さ)がわかると、三角形の外接円の半径を計算することができます。三角形の内角の正弦(サイン)とその対辺の長さの関係は辺の長さ/正弦が、外接円の直径(半径の2倍)になります。さらに、三角形の3辺の積を半径の4倍で割ることにより、三角形の面積を計算することができます。
正弦定理を使った三角形の面積の計算
- r = norm_ab / (sympy.sin(theta_ab)*2)
- tri_4=norm_a * norm_b * norm_ab/(r*4)
- display(Math(r'三角形の面積=%s' % sympy.latex(tri_4)))
内積と使う方法
そもそも、2つのベクトルの要素がわかれば、外積が使えなくても内積を使って面積を計算することができます。三角形の面積は、2つの辺のノルムの2乗の合計から内積の2乗を差し引いた結果の平方根が面積になります。
内積を使った三角形の面積の計算
- tri_5 = sympy.sqrt(norm_a **2 * norm_b **2 - dot_ab ** 2)/2b
- display(Math(r'三角形の面積=%s' % sympy.latex(tri_5)))
答えはいずれも$\frac{9\sqrt{3}}{2}$になります。
外積により6面体の体積を計算する
ベクトルs_a,s_bが張る平行六面体の体積は、次の式で計算することができます。
平行六面体の体積はs_aとs_bから計算した外積のベクトルとs_cの内積の絶対値となります。数式であらわすと次の計算をすることになります。
V=|(s_a×s_b)・s_c|
ベクトルの外積と内積から平行六面体の体積を計算する
- s_a = sympy.Matrix([1, 2, -1])
- s_b = sympy.Matrix([3, 1, 4])
- s_c = sympy.Matrix([1, 0, -1])
- cross_ab=s_a.cross(s_b)
- v_abc=cross_ab.dot(s_c)
- display(Math(r'外積=%s' % sympy.latex(cross_ab)))
- display(Math(r'体積=%s' % sympy.latex(v_abc)))
結果は同じです。