Pythonで行列の和を計算する

行列の定義と和の計算

リストによる定義と計算

Pythonで行列の計算をするときは、NumPyやSymPyモジュールを使うことが一般的で実用的ではありませんが、計算の流れを知るためリストによる表現からはじめます。ここでは、2つの行列をリストm_a、m_bとして定義して、2つの行列の和を求めます。それでは、行列を定義します。

行列の定義
  1. m_a = [[3, 2, 4],
  2. [5, 1 ,2],
  3. [3, 4 ,5]]
  4. m_b = [[1, 3, 2],
  5. [6, 2, 4],
  6. [2, 8, 3]]

行列の和は、要素同士の合計なので、はじめに合計を計算するための配列m_s1を空のリストとして定義し、for文で各要素の合計を計算した結果をappendメソッドでリストに追加します。

リストによる行列の和 ～ 最も単純な方法
  1. m_add1 = []
  2. for row in range(len(m_a)):
  3. temp = []
  4. for col in range (len(m_a[0])):
  5. temp.append(m_a[row][col]+m_b[row][col])
  6. m_add1.append(temp)
  7. m_add1

結果は次の通り、うまく計算することができました。

[[4, 5, 6], [11, 3, 6], [5, 12, 8]]

しかし何ともさえない方法なので、zip関数を使って2つのリストから同時に要素を取り出す方法を試してみます。

行列の和 ～ PythonらしくZipを使う方法
  1. m_add2 = []
  2. for row_a, row_b in zip(m_a, m_b):
  3. temp = []
  4. for elm_a,elm_b in zip(row_a,row_b):
  5. temp.append(elm_a + elm_b)
  6. m_add2.append(temp)
  7. m_add2

結果は、同じです。少しPythonらしくなりましたが、さらにリスト内包表記を使って計算します。

リスト内包表記による行列の和
  1. m_add3 = [[elm_a + elm_b for elm_a, elm_b in zip(row_a,row_b)] for row_a,row_b in zip(m_a,m_b)]
  2. m_add3

1行で計算できるのでとても便利ですが、リスト内包表記は2つのリストを扱うとわかりにくくなるのが難点です。

lambda式による行列の和
  1. m_add4=list(map(lambda row_a,row_b: list(map(lambda elm_a, elm_b:elm_a+ elm_b,row_a,row_b)), m_a, m_b))
  2. m_add4

こちらも結果は同じです。

リストを使った計算はPythonのプログラミングの練習にはなりますが手間がかかるので、行列の計算にはNumPyモジュールを使うのが一般的です。

NumPyによる定義と計算

NumPyモジュールの配列にはndarrayとmatrixの2つの形式があり、表記の仕方が異なります。まず、一般的なndarrayからです。ndarrayにはベクトル演算という機能があり、同じサイズの配列の算術演算では、同位要素（同じ場所の要素）ごとに計算されます。

NumPyのインポートと、ndarrayによる行列の定義
  1. import numpy as np
  2. na_a = np.array([[3, 2, 4],
  3. [5, 1 ,2],
  4. [3, 4 ,5]])
  5. na_b = np.array([[1, 3, 2],
  6. [6, 2, 4],
  7. [2, 8, 3]])
  8. na_add = na_a + na_b
  9. na_add

結果は、次の通り計算結果はndarray形式になります。

sympyによる行列の数値計算

array([5, 7, 9])となります。次に、matrixによる方法です。

NumPyのmatrixによる行列の定義
  1. nm_a = np.matrix([[3, 2, 4],
  2. [5, 1 ,2],
  3. [3, 4 ,5]])
  4. nm_b = np.matrix([[1, 3, 2],
  5. [6, 2, 4],
  6. [2, 8, 3]])
  7. nm_add = nm_a + nm_b
  8. nm_add

結果は次の通り計算結果はmatrix形式になります。

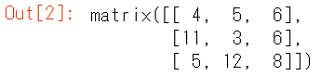
sympyによる行列の数値計算

SymPyによる定義と計算

SymPyはPython library for symbolic mathematicsといわれるように、代数を扱うことができます。sympy.matrixによりベクトルを定義し、合計します。Pythonは変数を明示的に定義しなくてもよい仕様になっていますが、SymPyでは、s_a、s_bのようにsympy.symbolsとして定義する必要があります。

SymPy Matrixによる行列の定義と和の計算
  1. import sympy
  2. sn_a, sn_b = sympy.symbols('s_a s_b')
  3. sn_a = sympy.Matrix([[3, 2, 4],
  4. [5, 1 ,2],
  5. [3, 4 ,5]])
  6. sn_b = sympy.Matrix([[1, 3, 2],
  7. [6, 2, 4],
  8. [2, 8, 3]])
  9. sn_add = sn_a + sn_b
  10. sn_add

結果は次の通り。

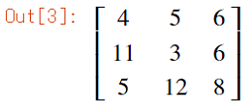
sympyによる行列の数値計算

これだけだと、わざわざ変数を定義するだけ手間がかかるだけですが、SymPyのすごさは、次のような代数計算ができることです。

Sympy Matrixによる行列の和の代数計算
  1. sympy.var('a_x1,a_x2,a_x3,a_y1,a_y2,a_y3,a_z1,a_z2,a_z3')
  2. sympy.var('b_x1,b_x2,b_x3,b_y1,b_y2,b_y3,b_z1,b_z2,b_z3')
  3. sa_a = sympy.Matrix([[a_x1,a_x2,a_x3],
  4. [a_y1,a_y2,a_y3],
  5. [a_z1,a_z2,a_z3]])
  6. sa_b = sympy.Matrix([[b_x1,b_x2,b_x3],
  7. [b_y1,b_y2,b_y3],
  8. [b_z1,b_z2,b_z3]])
  9. sa_add = sa_a+sa_b
  10. sa_add

ここでは、sv_sで2つのベクトルの和を計算しており、その中身は変数で格納されています。

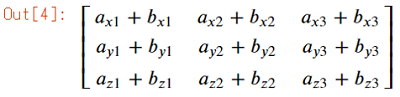
sympyによる行列の代数計算

次に、変数が格納されているベクトルにsubsメソッドで数値をしてすると、前例のように計算することができます。

Sympy Matrixの代数計算に数値を代入
  1. sa_add.subs([(a_x1, 3), (a_x2, 2),(a_x3, 4),(a_y1, 5), (a_y2, 1), (a_y3, 2), (a_z1, 3),(a_z2, 4), (a_z3, 5),
  2. (b_x1, 1), (b_x2, 3),(b_x3, 2),(b_y1, 6), (b_y2, 2), (b_y3, 4), (b_z1, 2),(b_z2, 8), (b_z3, 3)])

上手く計算することができました。