Pythonで行列の積を計算する

行列の定義と積の計算

リストによる定義と計算

Pythonで行列の計算をするときは、NumPyやSymPyモジュールを使うことが一般的で実用的ではありませんが、計算の流れを知るためリストによる表現からはじめます。ここでは、2つの行列をリストl_a、l_bとして定義して、2つの行列の積を求めます。

リストで行列を定義して、積を計算する

3×3のように行数と列数が等しい正方行列を2次元の配列として定義し、行列の積の定義により計算します。

リストによる行列の積 ～ 正方行列

1. l_a = [[1, -1, 2],
2. [2, -2 ,1],
3. [3, 1 ,-1]]
4. l_b = [[2, 1, 3],
5. [1, 1, 2],
6. [-1, 2, 3]]
7. dim = len(l_a)
8. l_mult = []
9. for row in range(dim):
10. temp = []
11. for col in range(dim):
12. elm = 0
13. for nth in range(dim):
14. elm += (l_a[row][nth]*l_b[nth][col])
15. temp.append(elm)
16. l_mult.append(temp)
17. l_mult

[[-1, 4, 7], [1, 2, 5], [8, 2, 8]]

行列の積は、要素同士の合計なので、はじめに合計を計算するための配列l_multを空のリストとして定義し、for文で各要素の合計を計算した結果をappendメソッドでリストに追加します。正しく計算されますが、for文が3つもネストしてしまい、何ともさえない方法になってしまいました。

行数と列数が異なる行列同士の積の計算

l_c（左側）を2行4列、l_d（右側）を4行3列の行列として配列を定義します。左側の列数と右側の行数が一致していないとエラーとなりますが、ここでは正しく定義されていることを前提とします。

リストによる行列の積 ～ n×m

1. l_c = [[1, -1, 2, 1],
2. [2, 0 ,3, 1]]
3. l_d = [[2, 1, -1],
4. [-1, 1, 0],
5. [-2, 1, 3],
6. [0, 1, 1]]
7. dim_r_a = len(l_c)
8. dim_c_a = len(l_c[0])
9. dim_r_b = len(l_d)
10. dim_c_b = len(l_d[0])
11. l_mult = []
12. for row in range(dim_r_a):
13. temp = []
14. for col in range(dim_c_b):
15. elm = 0
16. for nth in range(dim_c_a):
17. elm += (l_c[row][nth]*l_d[nth][col])
18. temp.append(elm)
19. l_mult.append(temp)
20. l_mult

[[-1, 3, 6], [-2, 6, 8]]

zip関数を使いネストを減らす

zip関数を使って2つのリストから同時に要素を取り出す方法を試してみます。

リストでzip関数を使った行列の積

1. l_mult=[]
2. for row in l_c:
3. temp=[]
4. for col in zip(*l_d):
5. elm=0
6. for row_nth,col_nth in zip(row,col):
7. elm+=row_nth*col_nth
8. temp.append(elm)
9. l_mult.append(temp)
10. l_mult

[[-1, 3, 6], [-2, 6, 8]]

上記の通り、うまく計算することができました。

リスト内包表記による行列の積の計算

zip関数を使い行列の積を計算できたので、これをリスト内包表記にしてみます。

リスト内包表記による行列の積の計算

1. l_a = [[1, -1, 2],
2. [2, -2 ,1],
3. [3, 1 ,-1]]
4. l_b = [[2, 1, 3],
5. [1, 1, 2],
6. [-1, 2, 3]]
7. l_c = [[1, -1, 2, 1],
8. [2, 0 ,3, 1]]
9. l_d = [[2, 1, -1],
10. [-1, 1, 0],
11. [-2, 1, 3],
12. [0, 1, 1]]
14. def l_mult_com(left,right):
15. return [[sum([row*col for row,col in zip(rows, cols) ]) \
16. for cols in zip(*right)] for rows in left]
18. print(l_mult_com(l_a,l_b))
19. print(l_mult_com(l_c,l_d))

[[-1, 4, 7], [1, 2, 5], [8, 2, 8]]
[[-1, 3, 6], [-2, 6, 8]]

標記の都合上、行を分割しましたが1行で表記することができました。どれくらい早くなるか試したくなります。

NumPyによる定義と計算

ndarray形式による行列の積の計算

NumPyモジュールの配列にはndarrayとmatrixの2つの形式がありますが、ここではndarray形式を取り扱います。

正方行列の積の計算

ndarrayにはベクトル演算という便利な機能があるので早速活用してみます。はじめに正方行列からです。n_aの行数を次元数として定義します。

Numpyのベクトル計算を使った行列の定義と積の計算

1. import numpy as np
2. n_a = np.array([[1, -1, 2],
3. [2, -2 ,1],
4. [3, 1 ,-1]])
5. n_b = np.array([[2, 1, 3],
6. [1, 1, 2],
7. [-1, 2, 3]])
8. dim= n_a.shape[0]
9. n_mult=np.empty((dim,dim))
10. for row in range(dim):
11. for col in range(dim):
12. n_mult[row,col ] = sum(n_a[row, :]*n_b[:, col])
13. n_mult

array([[-1.,  4.,  7.],
       [ 1.,  2.,  5.],
       [ 8.,  2.,  8.]])

12. n_a（左側の行列）の行の各要素と、n_bの列の各要素は、n_a[row, :]*n_b[:, col]で一気に計算することができます。この機能をNumPyのベクトル計算といいます。

n×m型同士の行列の積の計算

正方行列でない行列同士の掛け算は、n_c（左側の行列）の列数と、n_d（右側の行列）の行数が等しく、計算結果はn_cの行数×n_dの列数となります。

1. import numpy as np
2. n_c = np.array([[1, -1, 2, 1],
3. [2, 0, 3, 1]])
4. n_d = np.array([[2, 1, -1],
5. [-1, 1, 0],
6. [-2, 1, 3],
7. [0, 1, 1]])
8. dim_r_c = n_c.shape[0]
9. dim_c_c = n_c.shape[1]
10. dim_r_d = n_d.shape[0]
11. dim_c_d = n_d.shape[1]
12. n_mult=np.empty((dim_r_c,dim_c_d))
13. for row in range(dim_r_c):
14. for col in range(dim_c_d):
15. n_mult[row,col ] = sum(n_c[row, :]*n_d[:, col])
16. n_mult

array([[-1.,  3.,  6.],
       [-2.,  6.,  8.]])

関数を使った行列の積の計算

上記の結果を関数にすると次の通りになります。

NumPyモジュールを使った行列の積を求める関数

1. def multi(left,right):
2. if left.shape[1]!=right.shape[0]:
3. raise ValueError
4. multi_n=np.empty((left.shape[0],right.shape[1]))
5. for row in range(left.shape[0]):
6. for col in range(right.shape[1]):
7. multi_n[row,col ] = sum(left[row, :]*right[:, col])
8. return multi_n
10. print(multi(n_a,n_b))
11. print(multi(n_c,n_d))

[[-1.  4.  7.]
 [ 1.  2.  5.]
 [ 8.  2.  8.]]
[[-1.  3.  6.]
 [-2.  6.  8.]]

NumPyの演算子や関数を使った行列の積の計算

@演算子による行列の積

@演算子を使うと簡単に行列の積を計算することができます。

@演算子による行列の積の計算

1. print(n_a@n_b)
2. print(n_c@n_d)

[[-1  4  7]
 [ 1  2  5]
 [ 8  2  8]]
[[-1  3  6]
 [-2  6  8]]

dotメソッドを使った行列の計算

NumPyではdotメソッドを使うと行列の積を計算することができます。

NumPyのdotメソッドを使った行列の計算

1. print(np.dot(n_a,n_b))
2. print(np.dot(n_c,n_d))

[[-1  4  7]
 [ 1  2  5]
 [ 8  2  8]]
[[-1  3  6]
 [-2  6  8]]

こちらの各要素には小数点がついていません。

SymPyによる定義と計算

SymPyモジュールを使って行列の積を計算する

SymPyはPython library for symbolic mathematicsといわれるように、代数を扱うことができます。sympy.matrixによりベクトルを定義し、合計します。Pythonは変数を明示的に定義しなくてもよい仕様になっていますが、SymPyでは、sn_a、sn_bのようにsympy.varとして定義する必要があります。

Sympyのインポートと、Matrixによるベクトルの定義

1. import sympy
2. sn_a = sympy.Matrix([[1, -1, 2],
3. [2, -2 ,1],
4. [3, 1 ,-1]])
5. sn_b = sympy.Matrix([[2, 1, 3],
6. [1, 1, 2],
7. [-1, 2, 3]])
8. sn_add = sn_a * sn_b
9. sn_add

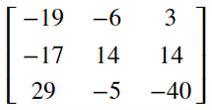
SymPyモジュールを使って代数的に行列の積を計算する

SymPyで代数的に行列の積を計算する

これだけだと、わざわざ変数を定義するだけ手間がかかるだけですが、SymPyのすごさは、次のような代数計算ができることです。

SymPyによる行列の積の代数計算

1. sa_a=sympy.var('a_x1,a_x2,a_x3,a_y1,a_y2,a_y3,a_z1,a_z2,a_z3')
2. sa_b=sympy.var('b_x1,b_x2,b_x3,b_y1,b_y2,b_y3,b_z1,b_z2,b_z3')
4. sv_a = sympy.Matrix([[a_x1,a_x2,a_x3],
5. [a_y1,a_y2,a_y3],
6. [a_z1,a_z2,a_z3]])
7. sv_b = sympy.Matrix([[b_x1,b_x2,b_x3],
8. [b_y1,b_y2,b_y3],
9. [b_z1,b_z2,b_z3]])
10. sa_multi= sv_a*sv_b
11. sa_multi

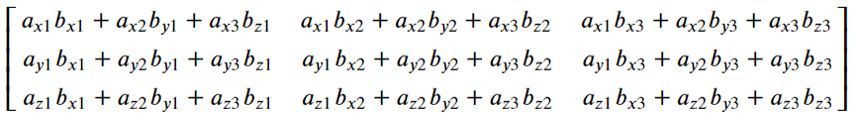
代数的に計算した行列の積の結果に数値を代入する

次に、変数が格納されているベクトルにsubsメソッドで数値をしてすると、前例のように計算することができます。

Sympy Matrixの代数計算に数値を代入

1. sa_multi.subs([(a_x1, 1), (a_x2, -1),(a_x3, 2),(a_y1, 2), (a_y2, -2), (a_y3, 1), (a_z1, 3),(a_z2, 1), (a_z3, -1),
2. (b_x1, 2), (b_x2, 1),(b_x3, 3),(b_y1, 1), (b_y2, 1), (b_y3, 2), (b_z1, -1),(b_z2, 2), (b_z3, 3)])

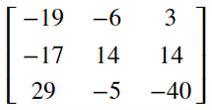
結果は同じように縦のベクトルで戻ります。