Pythonで行列式の値を計算する

Pythonの機能を使い、定義通り行列式の値を計算する

PythonのNumpyモジュールやSymPyモジュールには行列式を計算する関数が用意されていますが、はじめに考え方を理解するため、リストから定義通りに計算してみます。

2次元の行列の行列式の計算

2次元（2×2）の行列の行列式は、次のようにpythonの配列でいうと0行0列×1行1列と0行1列×1行0列の差になります。

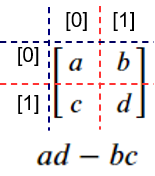
したがって、次のような簡単なプログラムで行列式を計算することができます。

2次元の行列式

1. m = [[1, 2],
2. [3, 4]]
3. det = m[0][0]*m[1][1]-m[0][1]*m[1][0]
4. det

3次元の行列の行列式の計算

3次元の行列（3×3）の場合、サラスの公式を使い行列式を計算することができます。

図のとおり、$a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}$の計算をします。つまり、縦方向1列目から3列目3つの列に対して、3つの行を(1,2,3)、(2,3,1) 、(3,1,2)のように順番を変えて対応させます（図では赤い右下向きの矢印）。さらに、（3,2,1）、(1,3,2) 、(2,1,3) （図では青い右上向きの矢印）のように順番を変えて対応させます。

結果として1列目の1,2,3の3つに対し1つを選び、2列目には残りのうち2つから1つ選び、3列目は最後の1つを選びます。結果として6通り（3!）の組み合わせの積を合計して計算します。このとき、図の通り右下の方向に向かう積の計算ではプラス、左下に向かう積の計算ではマイナスにして集計します。

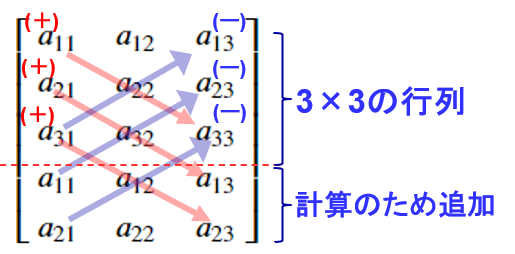
式をそのまま入力しても差し支えありませんが、野暮ったくなるので、3行目の下に1行目と2行目を結合して、それぞれ4行目、5行目とします。すると、右下の方向に向かうプラスの部分と左下に向かうマイナスの部分が1行ずつをループすることで、3つの要素の積を変数detで集計することができます。

3次元の行列式をサラスの公式で計算する

1. m = [[2, 3, 5],
2. [5, 9, 9],
3. [3, 8, 8]]
4. mm = m+[m[0]]+[m[1]]
5. det = 0
7. for i in range(3):
8. det += mm[i][0]*mm[i+1][1]*mm[i+2][2]
9. det -= mm[i][2]*mm[i+1][1]*mm[i+2][0]
10. print(det)

結果は26になります。

4次元以上の行列の場合

4次元の行列の場合も4つの行に対し、4つの列のすべての組み合わせの積を計算し、集計することで行列式を求めることができます。しかし、プラス、マイナスの符号が3次元のように単純に方向だけで決めることができません。

そこでsgnという関数を作り、4つの列の組み合わせがプラスかマイナスかを判断することからはじめます。

Sgnの計算

$a_{11}a_{22}a_{33} a_{44}$や$a_{12}a_{21}a_{33} a_{44}$のように4つの行から4つの列のすべての組み合わせの要素の積を計算します。列だけを取り出すと(1,2,3,4)、(2,1,3,4)のようになり、その組み合わせは4次元だと4の階乗(4!=4×3×2×1=24) 通りになります。

ここで、 (1,2,3,4)という基本的な形から、2つの要素を選んで入れ替えることを置換といいます。そして、ある列の番号の組み合わせが、(1,2,3,4)からの置換の回数でプラスかマイナスかを判断します。具体的には、置換の回数が偶数の場合にはプラス、奇数の場合にはマイナスです。

図の通り、列の組み合わせが(2,1,3,4)の場合は置換が1回でマイナス、(2,3,1,4)は2回でプラス、(3,2,1,4)は3回でマイナスという具合です。

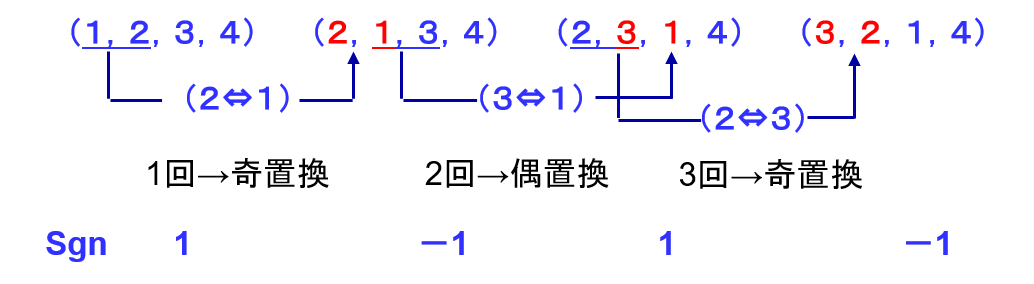
それでは、これをプログラムに落とすときの1つの考え方として、4つならんだ数字のそれぞれについて、その数字より左側に自分より大きな数字がいくつあるかで判断します。たとえば、(3,2,1,4)だと、3には左には数字はそもそもないので0、2の場合は3が1つ、1の場合は3と2の2つ、4の場合は0となり、合計すると3になります。

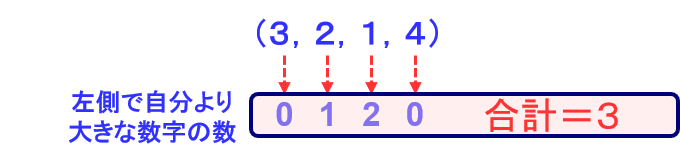
このためサインはマイナスになり、上記の結果と一致します。なぜこの考え方で計算できるかは、ある数字が左側の自身より大きな数値と置換を繰り返していくと、最後に(0,1,2,3)になっていくまでの回数と一致することを考えると理解しやすいと思います。

サインを計算する関数

1. def sgn(L):
2. sum_of_bigger = 0
3. for index in range(len(L)-1):
4. for left in range(index+1, len(L)):
5. if L[index] > L[left]:
6. sum_of_bigger += 1
7. if sum_of_bigger % 2 == 0:
8. return 1
9. else:
10. return -1

結果は次の通り、うまく計算することができました。

サインを計算する関数を実行

1. l0 = [1, 2, 3, 4]
2. l1 = [2, 1, 3, 4]
3. l2 = [2, 3, 1, 4]
4. l3 = [3, 2, 1, 4]
5. print(sgn(l0))
6. print(sgn(l1))
7. print(sgn(l2))
8. print(sgn(l3))

1
-1
1
-1

このようにしてsgnという関数を作り、引数として列の組み合わせを配列として指定すると1か-1が判断され、戻り値として返ります。

4次元の行列の行列式の計算

4次元の行列の行列式を計算するためには、1行目から4行目までに対して、1列目から4列目までの(1,2,3,4)(1,3,2,4)のように順番を変えた24通り(4!)の組み合わせの積をsgnを考慮しながら合計します。具体的には、カウンタをi1,i4まで取り、for文を4回ネストすることにより積を求めて、変数detで計算結果を集計します。

4次元の行列式の計算

1. m = [[3, 2, -2, 2],
2. [2, 3, -4, 3],
3. [4, 3, -3, 2],
4. [2, 5, 2, 4]]
6. det = 0
7. for i1 in range(4):
8. for i2 in range(4):
9. for i3 in range(4):
10. for i4 in range(4):
11. l = list([i1, i2, i3, i4])
12. if len(list(set(l))) == 4:
13. det += (sgn(l)*m[0][i1]*m[1][i2]*m[2][i3]*m[3][i4])
14. det

結果は45となり、正しい結果になります（後で関数を用いて確認します）。

4次元以上の行列の行列式の計算

インデックスの次元を増やす

4次元を超える場合も、4次元と同じ考え方で行列式を計算することができます。しかし、このときfor文のネストの回数が次元によって変わるので、いろいろな次元に対応したプログラムを作る必要があります。そこで、問題を簡単にするためにn個の行に対して列の組み合わせを網羅した配列を作ります。

考え方は、2次元の場合は[1 , 2]、[2 , 1]の2通りになりますが、3次元にするときには、2つの配列の2つの要素の先頭と真ん中と末尾の3か所に3を埋め込んでいきます。結果的に2つの配列それぞれに対し、3か所に3を埋め込むので6つの配列ができあがります。4次元にするときは、6つの配列のそれぞれに4か所に4を埋め込んでいくことになります。結果的に24個の配列が出来上がります。このように、n次元の行列式を計算するためにはn!個の配列が必要になります。

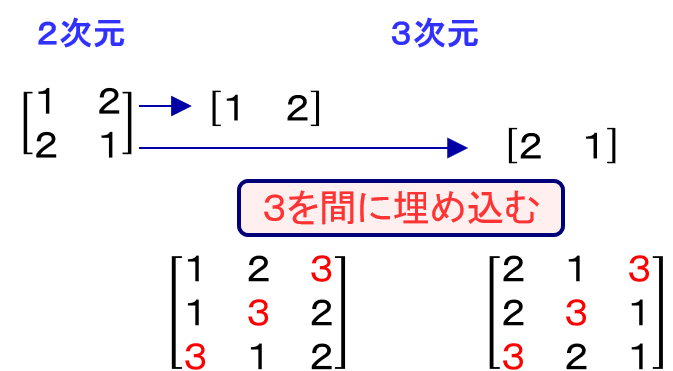
内部モジュール（次元を増やす）　[[1]]→[[1,2],[2,1]]

1. import copy
2. def d_plus(index):
3. temp = []
4. dim=len(index[0])+1
5. for i in range(len(index)):
6. for j in reversed(range(dim)):
7. row = copy.deepcopy(index[i])
8. row.insert(j, dim)
9. temp.append(row)
10. return sorted(temp)
13. index = [[1, 2], [2, 1]]
14. d_plus(index)

[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

ここでは、2×2の行列をindexという配列でコールした場合、各行をrowという作業域を作るためにディープコピーします。普通にコピーすると作業域を変更すると本体もその変更が及んでしまうためです。次に作業エリアの各要素の間に3の数字を埋め込んでいきます。

再帰関数を使ってn次元のインデックスを作成する

さらに、ここで作成したd_plusを2次元、3次元～n次元と順次呼び出します。このような場合に、再帰関数を使うと便利です。

d_plus関数を使ってindexを生成

1. def index_m(n,index=[[1]]):
2. if n ==1:
3. return index
4. else:
5. return index_m(n-1,d_plus(index))

この関数index_mには、引数として次元と、今の次元の行列を指定します。ここで、ルーチンに入ると、nが1でなかれば、すぐに自身の関数index_mを引数を1ずつ減らして呼び出します。nが1になったら今度は関数が次々と次元を増やして行列を返します。

では、1次元から2次元、2次元から3次元というように次元数を1増やすときにどうするかという単純な仕組みを考え、この関数を次元数に応じて関数のなかから呼び出すことで結果的にn次元の複雑な組み合わせを作っていきます。

はじめにn=4として4次元の配列を作りたいとしてindex_mをコールします。ここで、indexは何も指定していないので、デフォルトで[1]が入ります。ここでelseに入り先ほどのndex_mをコールします。すると[[1,2],[2,1]]が返ります。次にn-1の3として、今の2次元の配列を引数としてindex_mをコールします。同じようにn=3,n=2,n=1としてこの関数が呼び出され、最後にindexつまり4次元の組み合わせが帰されます。

4次元以上の行列式の計算

これまで作成した組合せのリストをつくるindex_m関数と、その組み合わせの置換の種類を計算するsgn関数を使い行列式を計算します。

4次元以上の行列式の計算

1. dem = len(m)
2. index = index_m(dem)
3. det=0
4. for i,row in enumerate(index):
5. product = 1
6. for col in range(dem):
7. product *= m[col][row[col]-1]
8. det += sgn(row)*product
9. det

45

イテレータツールによる組み合わせの作成

配列の組み合わせを作成するために、index_m関数のようにかなり複雑なプログラムを作成する必要があります。これに対して、イテレータ生成関数(itertools)を使うと簡単に配列を作ることができます。

イテレータ―ツールによる組み合わせの作成

1. import itertools
2. l = list(itertools.permutations(range(4)))
3. l

イテレータ生成関数を使うと、簡単に行列式を計算することができます。しかし、これではイテレータの良いところの半分しか使えていません。

前のプログラムのlistを外すとobject at・・・といように実際のリストではないものが返されます。次に、nextを1回実行するごとに、組み合わせが1つずつ返されます。

イテレータ＾ツールの本来の使い方

1. i = itertools.permutations(range(4))
2. print("itertoolsのアウトプット:", i)
3. print("1回目:", next(i))
4. print("2回目:", next(i))
5. print("3回目:", next(i))

itertoolsのアウトプット: 
1回目: (0, 1, 2, 3)
2回目: (0, 1, 3, 2)
3回目: (0, 2, 1, 3)

4次元くらいであれば特に問題はありませんが、もっと次元数が大きくなるとリストとして持つと、その分のメモリを使ってしまうので、コンピュータに負荷をかけてしまいます。そこで、次の通りにします。ここで、for row in index:のループを回すごとにnextが実行されます。イテレータ生成関数(itertools)で1つの組合せを作り積の計算が終わったら、その配列の組み合わせはメモリから消えてしまいます。このためメモリを有効に使うことができます。

イテレータ生成関数(itertools)を使った4次元以上の行列式の計算

1. import itertools
2. dem = len(m)
3. index = itertools.permutations(range(dem))
4. det = 0
5. for row in index:
6. product = 1
7. for col in range(dem):
8. product *= m[col][row[col]]
9. det += sgn(row)*product

これだけのプログラムで行列式を計算することができます。結果は45になります。

Numpyのdet関数で行列式を計算する

NumpyモジュールにはLinear algebra（代数）機能があり、使うときには numpy.linalgのあとに関数を指定します。例えば、行列式は次の通り、np.linalg.det(配列)とします。すると次の通り、簡単に行列を計算することができます。ちなみにdetとは

determinantの略です。

Numpyのdet関数による行列式の計算

1. import numpy as np
2. m_n=np.array([[3,2,-2,2],
3. [2,3,-4,3],
4. [4,3,-3,2],
5. [2,5,2,4]])
6. np.linalg.det(m_n)

Sympyモジュールを使うときには、detはメソッドを使います。

Sympyのdetメソッドによる行列式の計算

1. import sympy
2. # sympy.init_printing()
3. s_a = sympy.symbols('s_a')
4. s_a = sympy.Matrix([[3,2,-2,2],
5. [2,3,-4,3],
6. [4,3,-3,2],
7. [2,5,2,4]])
8. sympy.det(s_a)

結果はいずれも45になります。