Pythonで余因子行列を計算する

余因子行列の計算

余因子行列とは

n次正方行列に対してi行j列を取り除いた行列を考えます（minor matrixということがあります）。行列の行列式を計算し、行と列の合計が奇数の場合にはマイナスします。その行と列を取り除いた要素の行列式をいいます。ただし、このときの符号はi+jが奇数の時には-を付けます。この値を要素(i,j)に対する余因子といいます。そしてこの余因子を全ての要素に対して計算し、i行j列の要素とする行列を余因子行列（cofactor matrix）といいます。

なぜ、このような複雑な計算をする必要があるかはさておき、まずは余因子行列を計算するプログラムを作成します。

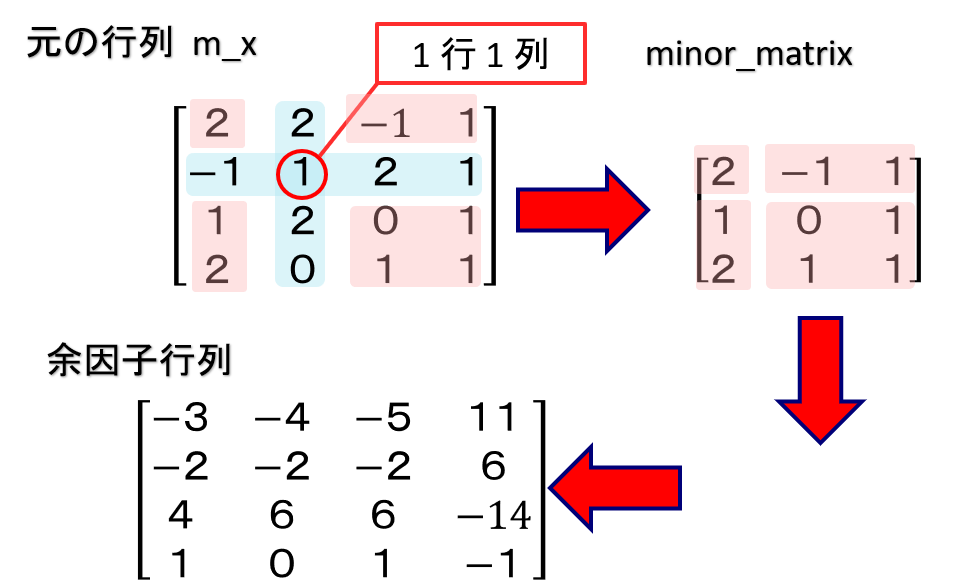
余因子行列の計算

行列の定義

4行4列の行列を定義します。ここでは2次元の配列とします。

行列の定義

m_x =[[ 2, 2,-1, 1],
[-1, 1, 2, 1],
[ 1, 2, 0, 1],
[ 2, 0, 1, 1]]

minor matrixの計算

4行4列の行列に対し、i行j列を取り除いた行列を計算する関数を作成します。

余因子の計算

def minor_submatrix(m, i, j):
mtrx = []
for row in range(len(m)):
if row != i:
mtrx_rows = []
for col in range(len(m[0])):
if col != j:
mtrx_rows.append(m[row][col])
mtrx.append(mtrx_rows)
return mtrx
minor_submatrix(m_x,1,1)

[[2, -1, 1], [1, 0, 1], [2, 1, 1]]

図と比べると、正しく計算されたことがわかります。

行列式の計算

余因子を計算するためには、minor matrixの行列式を計算する必要があります。ここでは以前作成したdet関数を使います。

Pythonで行列式を計算する

import copy
def d_plus(index):
temp = []
dim=len(index[0])+1
for i in range(len(index)):
for j in reversed(range(dim)):
row = copy.deepcopy(index[i])
row.insert(j, dim)
temp.append(row)
return sorted(temp)
def index_m(n,index=[[1]]):
if n ==1:
return index
else:
return index_m(n-1,d_plus(index))
def sgn(L):
sum_of_bigger = 0
for index in range(len(L)-1):
for left in range(index+1, len(L)):
if L[index] > L[left]:
sum_of_bigger += 1
if sum_of_bigger % 2 == 0:
return 1
else:
return -1
def det(m):
dem = len(m)
index = index_m(dem)
det=0
for i,row in enumerate(index):
product = 1
for col in range(dem):
product *= m[col][row[col]-1]
det += sgn(row)*product
return det

かなり面倒なプログラムになりますが、4次元以上の行列となると複雑な計算をする必要があります。

余因子の計算

行列式を求めることができたら、余因子の計算はminor matrixの行列式を計算し、i+jが偶数であれば加算、奇数であれば減算するだけの簡単な計算になります。ここではcofactor関数とします。

def cofactor(m,i,j):
return (-1)**(i+j)*det(minor_submatrix(m_x, i, j))
cofactor(m_x,1,0)

-2

余因子を計算することができました。

余因子行列の計算

cofactor関数では、元の行列の各要素にcofactor関数を適用するだけです。

def cofactor_matrix(m):
mtrx=[]
for i in range(4):
mtrx_rows=[]
for j in range(4):
mtrx_rows.append(cofactor(m,i,j))
mtrx.append(mtrx_rows)
return mtrx
cofactor_matrix(m_x)

[[-3, -4, -5, 11], [-2, -2, -2, 6], [4, 6, 6, -14], [1, 0, 1, -1]]

余因子の使い途

なぜ、余因子の計算はすこし面倒ですが、面白い計算に使えます。

行列式の計算

行列式の計算は前述のとおり、かなり複雑になります。ところが、余因子を使うと次のような面白い性質があります。

3次元の行列の場合、1行目の各要素とその余因子（2行×2列）の積の和を求めると元の行列の行列式と一致します。

3次元の行列式の計算は次の式で計算します。

$a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}$

この式と図を比べると確かに計算結果は一致します。このことは4次元以上の行列にもあてはまります。このことから、再帰関数を使い行列式を計算することを考えます。この関数では前に作成したminor_submatrixを使います。

def det_r(m):
dim=len(m)
det=0
if dim==1:
return m[0][0]
else:
for i in range(dim):
det+=(-1)**i*m[0][i]* det_r(minor_submatrix(m,0,i))
return det
det_r(m_x)

-2

たったこれだけのプログラムで行列式を計算することができるのは驚きです。