Pythonによる行基本変換と逆行列の計算

Pythonで掃き出し法を使い逆行列の計算をします。掃き出し法では、逆行列を求めたい元の行列に対し、行基本変換という行を単位に加減をする操作を繰り返します。そこで、以前に作成した行列の積や行列式を計算するプログラムを確認した上で、Pythonで行基本変換をするプログラムを作成し、これらのプログラムを適用することにより逆行列を計算します。

行列の積と行列式を計算する関数

行列の積と行列式を計算する関数を確認します。

行列の積の計算

行列の積を計算するmulti関数を作成します。引数で2つの行列をleft,rightという引数で指定します。

行列の積の計算

1. def multi(left,right):
2. l_mult=[]
3. for row in left:
4. l_temp=[]
5. for col in zip(*right):
6. elm=0
7. for row_nth,col_nth in zip(row,col):
8. elm+=row_nth*col_nth
9. l_temp.append(elm)
10. l_mult.append(l_temp)
11. return l_mult

行列式の計算

行列式を計算するdet_r関数を作成します。ここでは、余因子行列を利用するため、行列から特定の行列を取り除くためminor_submatrixを利用します。

行列式の計算

1. def minor_submatrix(m, i, j):
2. return [[m[row][col] for col in range(4) if col!=j ]
3. for row in range(4) if row!=i ]
5. def det_r(m):
6. dim=len(m)
7. det=0
8. if dim==1:
9. return m[0][0]
10. else:
11. for i in range(dim):
12. det+=(-1)**i*m[0][i]* det_r(minor_submatrix(m,0,i))

minor_submatrixで、ある特定の要素を含む行と列を取り除いた行列を計算し、ここから余因子展開を使い行列式を計算します。再帰関数を使うと、これだけの簡単なコードで行列式の計算ができるのは驚きです。

行基本変換とその応用

掃き出し法の計算をするため、行基本変換をする変換行列について整理します。行列に対して、次の3つの操作を行基本変換といいます。

1. ある行と他の行を入れ替える
2. ある行をn倍する
3. ある行をn倍した値を他の行に加算する

これらの行基本変換を繰り返すことにより、逆行列を求めるなど複雑な計算をすることができます。行基本変換を行うためには、対象とする行列の左から変換行列という特別な行列を掛けます。そこで、変換行列を作成するプログラムを作成、これらを組み合わせて逆行列を計算します。

行基本変換の考え方

逆行列を計算したい行列m_xに対して、行に関わる変換を掛けるときには、図のような行列を左から掛けます。変換行列l_switchを例に、m_xとの関係でどのような結果になるかを考えます。

1行目に注目すると、l_switchは0列目と1列目の要素は0、2列目の要素は1が設定されています。このことは、計算結果においては1行目は0各要素が1倍されて1行目に加算されることを示します。0列目と0列目は0なので、0行目と1行目の要素は加算されず、結果的に2行目の要素で1行目の要素に置き換わります。

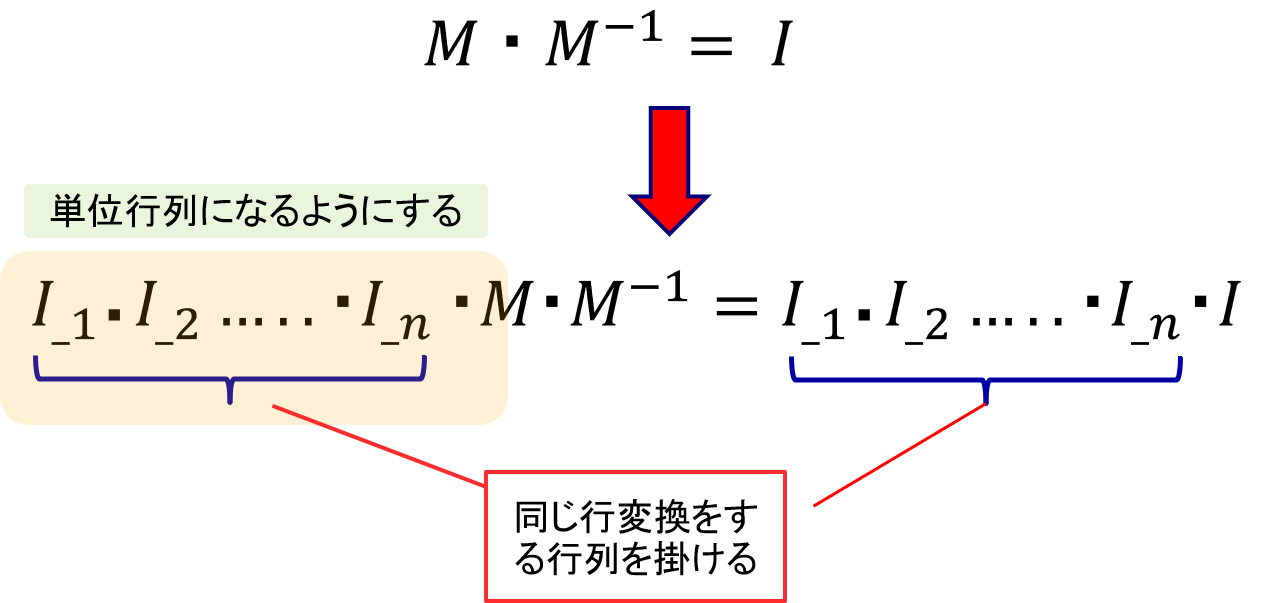
同様に、l_switch の2行目については1列目のみ1なので、結果的に1行目の要素が2行目に置き換わり、最終的に1行目と2行目が入れ替わることになります。

これらのことから、n行目に注目すると、計算結果のn行目の要素の値は、変換行列のn行目のm列の値×m行目の値の合計となります。これらのことから、次節で行基本変換を考えます。

行の入れ替え（Row switching）

行列のある行と別の行を入れ替える変換を考えます。ここでは、2行目と3行目を入れ替えます。前節の通り、2行目を1倍して3行目を置き換え、3行目を1倍し2行目を置き換えます。

行基本変換　行の入れ替え

1. l_switch=[[1, 0, 0],
2. [0, 0, 1],
3. [0, 1, 0]]
4. m_switch=multi(l_switch,m_x)
5. print(m_switch,' 行列式=',det_r(m_switch))

[[2, 4, -1], [3, 5, -1], [-2, -3, 1]]  行列式= -1

なお、この変換により行列式は元の行列式をマイナスした値になります。

ある行をn倍する（Row multiplication）

行列のある行をn倍する変換を考えます。ここでは1行目を2倍します。変換行列の考え方からすると、1行目の1列目が2で他の列は0なので、結果的に1行目が2倍されます。

行基本変換　行をn倍する

1. l_multi=[[2, 0, 0],
2. [0, 1, 0],
3. [0, 0, 1]]
4. m_multi=multi(l_multi,m_x)
5. print(m_multi,' 行列式=',det_r(m_multi))

[[4, 8, -2], [-2, -3, 1], [3, 5, -1]]  行列式= 2

なお、行列式の値は元の行列式のn倍になります。

行をn倍して別の行に加算（Row addition）

行列のある行をn倍して別の行に加える変換を考えます。ここでは、1行目を2倍して2行目に加えます。変換行列の考え方からすると、2行目に注目すると1列目が2、2列目が1なので、1行目を2倍して2列目の1倍に加算されることになります。

行基本変換　行をn倍して別の行に加算

1. l_plus=[[1, 0, 0],
2. [2, 1, 0],
3. [0, 0, 1]]
4. m_plus=multi(l_plus,m_x)
5. print(m_plus,' 行列式=',det_r(m_plus))

[[2, 4, -1], [2, 5, -1], [3, 5, -1]]  行列式= 1

少し意外かもしれませんが、行列式の値は1となります。

行をn倍して別の行のm倍に加算

前節の合わせ技で、行列のある行をn倍して別の行をm倍して加算します。ここでは、1行目を3倍して3行目を2倍した行に加算します。

行をn倍して別の行のm倍に加算

1. l_comp=[[1, 0, 0],
2. [0, 1, 0],
3. [3, 0, 2]]
4. m_comp=multi(l_comp,m_x)
5. print(m_comp,' 行列式=',det_r(m_comp))

[[2, 4, -1], [-2, -3, 1], [12, 22, -5]]  行列式= 2

この場合、行列式の値は加算される行に掛けられたm倍になります。

3次元の行列の逆行列を計算する

必要なモジュールの作成

単位行列を作成する関数

単位行列を作るeye関数を作成します。

#単位行列の作成

1. def eye(dim):
2. return [[1 if row==col else 0 for col in range(dim)] for row in range(dim)]
4. eye(3)

[[1, 0, 0], [0, 1, 0], [0, 0, 1]]

ある行列をn倍して、他の行をm倍したものに加算する関数

掃き出し法で逆行列を計算するうえで欠かせない行基本変換を組み合わせた関数を作成します。ある行をn倍して、他の行をm倍ものに加算します。この関数を使うと、ある行の任意の列の要素を0にすることができます。この関数で計算した行列を左から掛けることにより、行の加算の操作をすることができます。ここでは、multi_row行をmulti_times倍し、added_row行をadded_times倍したものに加えるようにします。

行列の加算

1. def row_m(multi_row,multi_times,added_row,added_times,dim):
2. transformed =eye(dim)
3. transformed[added_row][multi_row]=multi_times
4. transformed[added_row][added_row]=added_times
5. return transformed
7. multi(row_m(0,3,1,2,3),m_x)

[[2, 4, -1], [2, 6, -1], [3, 5, -1]]

行を交換する関数

掃き出し法で逆行列を計算するうえで欠かせない、もう1つの行基本変換をする関数を作成します。ここではp行目とa行目を入れ替えるための行列を作成します。この関数で計算した行列を左から掛けることにより、行の交換をすることができます。

行を入れ替える変換行列

1. def switch(p,a,dim):
2. switch_l= eye(dim)
3. switch_l[p][p]=0
4. switch_l[a][a]=0
5. switch_l[a][p]=1
6. switch_l[p][a]=1
7. return switch_l
9. multi(switch(0,1,len(m_x)),m_x)

[[-2, -3, 1], [2, 4, -1], [3, 5, -1]]

3次元の行列の逆行列を掃き出し法で計算する

掃き出し法の考え方と流れ

掃き出し法の考え方

行列$M$に対して逆行列$M^{-1}$を計算するための掃き出し法（Gaussian elimination）について、図に沿って考えます。$M\cdot M^{-1}=I$とすると、この両辺に行基本変換する行列を次々と掛けていきます。最終的にこれらの行列と$M$の積が単位行列になるようにすれば、右辺は$M$の逆行列になります。よって$M$と$I$に対して、同じ基本変換をする行列を掛けていき、最終ゴールとして左辺の$M$が$I$になるように工夫します。

プログラムの流れ

3次元の行列の逆行列を計算するため、次の手順で計算します。なお、行列は1行、2行と数えますが、Pythonの特質上0行、1行と0からカウントします。

結果的に一番下の2行目は、2列目以外の要素は0になります。

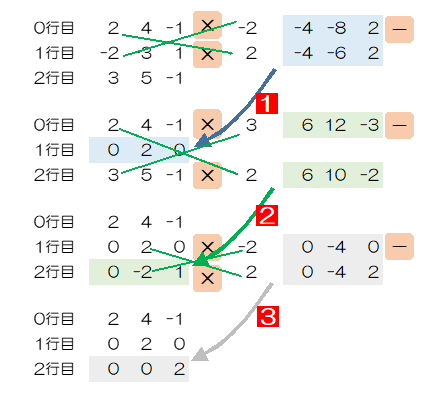
0の要素がある場合の処理

前節の0行0列の値が0の場合、0行目を使って他の行を0にすることができません。そこで、1行目以降で0列の要素の値が0でないものがあるときは、その行と1行目を置き換えます。

1. m_x=[[ 0, 4, -1],
2. [-2,-3, 1],
3. [ 3, 5, -1]]
5. org=m_x
6. inv=eye(3)
7. for i in range(2):
8. #追加開始
9. row_0=0
10. while org[i][i]==0: #消そうとしたとき0なら
11. row_0+=1
12. if row_0 >= 3-i:
13. raise ValueError("逆行列がありません")
14. t_s=switch(i,i+row_0,3)
15. print(t_s)
16. org=multi(t_s,org)
17. inv=multi(t_s,inv)
18. #追加終了
19. for j in range(i+1,3):
20. t=row_m(i,-org[j][i],j,org[i][i],3)
21. org=multi(t,org)
22. inv=multi(t,inv)
23. print(t,org)

[[0, 1, 0], [1, 0, 0], [0, 0, 1]]
[[1, 0, 0], [0, -2, 0], [0, 0, 1]] [[-2, -3, 1], [0, -8, 2], [3, 5, -1]]
[[1, 0, 0], [0, 1, 0], [-3, 0, -2]] [[-2, -3, 1], [0, -8, 2], [0, -1, -1]]
[[1, 0, 0], [0, 1, 0], [0, 1, -8]] [[-2, -3, 1], [0, -8, 2], [0, 0, 10]]

最後の行を使い、それ以外の行の値を0にする

3次元の行列で、最後の行の最終列以外の要素を0にする関数を作成します。

行列の最後の行の最終列以外を0にする

1. m_x=[[ 2, 4, -1],
2. [-2,-3, 1],
3. [ 3, 5, -1]]
5. org=m_x
6. inv=eye(3)
7. for i in range(2):
8. for j in range(i+1,3):
9. t=row_m(i,-org[j][i],j,org[i][i],3)
10. org=multi(t,org)
11. inv=multi(t,inv)
12. print(t,org)

[[1, 0, 0], [2, 2, 0], [0, 0, 1]] [[2, 4, -1], [0, 2, 0], [3, 5, -1]]
[[1, 0, 0], [0, 1, 0], [-3, 0, 2]] [[2, 4, -1], [0, 2, 0], [0, -2, 1]]
[[1, 0, 0], [0, 1, 0], [0, 2, 2]] [[2, 4, -1], [0, 2, 0], [0, 0, 2]]

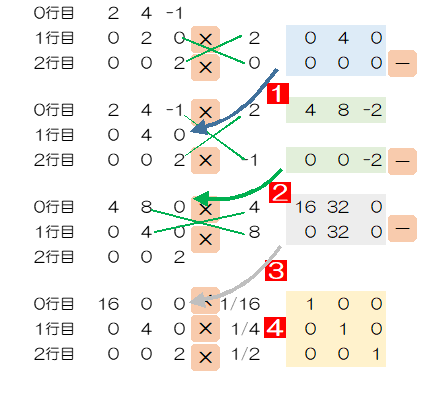
最後の行から順に単位行列に近づける

1. for i in range(-1,-3,-1):
2. for j in range(i-1,-4,-1):
3. t=row_m(i,-org[j][i],j,org[i][i],3)
4. org=multi(t,org)
5. inv=multi(t,inv)
6. print(t,org)
7. print(inv)

[[1, 0, 0], [0, 2, 0], [0, 0, 1]] [[2, 4, -1], [0, 4, 0], [0, 0, 2]]
[[2, 0, 1], [0, 1, 0], [0, 0, 1]] [[4, 8, 0], [0, 4, 0], [0, 0, 2]]
[[4, -8, 0], [0, 1, 0], [0, 0, 1]] [[16, 0, 0], [0, 4, 0], [0, 0, 2]]
[[-32, -16, 16], [4, 4, 0], [-2, 4, 4]]

単位行列に変換する

前節までで、対角行列に変換できたので、これを単位行列にするため、各要素をその値で割るようにします。

単位行列に変換

1. t_m=eye(3)
2. for i in range(3):
3. t_m[i][i]=1/org[i][i]
4. inv=multi(t_m,inv)
5. inv

[[-2.0, -1.0, 1.0], [1.0, 1.0, 0.0], [-1.0, 2.0, 2.0]]

逆行列を計算することができました。