浮動小数点型のしくみと整数部分の計算
Pythonで小数の演算をするときには浮動小数点型を使います。浮動小数点型は、整数だけではなく小数点以下の数字を扱うことができます。ただし、その仕組みは非常に複雑なので、ここでは簡単のため小数部分がない浮動小数点型の数値についての計算について探っていきます。
浮動小数点型の変数の定義
浮動小数点型の割り算、商、余りの計算
python での割り算、商、余りの計算
- qi = 10//3
- ri = 10 % 3
- di = 9/3
- print(q, type(q))
- print(r, type(r))
- print(d, type(d))
- qf = 10.3//3
- rf = 10.3 % 3
- df = 10.3/3
- print(qf, type(qf))
- print(rf, type(rf))
- print(df, type(df))
31 3.0 3.0 1.3000000000000007 3.4333333333333336
4. 整数同士の数値に対し//演算子を使って計算すると、商(割り算の結果小数点以下を切り捨て)を計算することができます。このとき、計算結果は整数型(int型)になります。
5. 同様に%演算子を使って計算すると、余りを計算することができます。このとき、計算結果は整数型(int型)になります。
6. 同様に/演算子を使って演算をすると、割り算の結果を求めることができます。このとき、割り切れたとしても計算結果は3.0のように表示され、浮動小数点型(float型)となります。
10. 演算の中に10.3のような小数が含まれる場合は、商や余りも浮動小数点型(float)になります。
11.12. 割り算の計算の中で計算結果が浮動小数点型になる場合、有効桁数が17桁程度になり、細かいところで誤差が発生します。この誤差は、浮動小数点型のデータの表し方の特徴によるものです。
浮動小数点の考え方
コンピュータはその用途により、10,000,000,000.5のように整数分部の桁数の大きな数値から、0.12345678のように小数点以下の桁数が多い数値まで、さまざまなデータを扱う必要があります。また、数値などのデータを1と0を区別するビットのカタマリとして処理しています。このため、コンピュータがデータの演算や記憶をするときは、使うことができるビット数が多ければ多いほど、桁数の大きな数値を扱ったり小数点以下の数値を精度よく計算したりすることができるわけです。
いっぽう、現在、多くのパソコンは64ビット版のWindowsやMacOSといったOS(オペレーティングシステム)を使っています。これは、64ビットのデータをカタマリとして1回で処理することができることを示しています。このため、数値を64ビットの中で表現することができれば、効率が良くデータを処理することができるのです。
このように、少しでも精度良く計算したいという要求と、64ビットのカタマリで数値を表現したいという、相反する要求がありますが、これらを両立させようとするものが浮動小数点演算です。64ビットの中で小数点の位置を固定してしまうと、10,000,000,000.5のような数値では小数以下の部分が無駄になってしまい、十分に大きな整数部分を表現することができなくなります。いっぽう、0.12345678のような数値では整数部分が無駄になってしまい、小数点以下の部分について十分な精度をもって表現することができなくなってしまいます。そこで、数字の桁数に合わせて小数点の位置を柔軟に移動(つまり浮動)させることで、限られた64ビットの中でいろいろな大きさの数字をうまく表現しようという作戦です。
ところで、少し前までは多くのパソコンは32ビット版のOSを使っていました。そこではデータを32ビットで表現する方法を採っていましたが、浮動小数点型はこのときの仕組みが基本となっています。前述のとおり、現在は64ビットOSが主流となりつつあるので、その倍のビット数を使い数値計算をすることができるようになりました。そこで、この仕組みを倍精度浮動小数点演算といい、現状、Pythonではこの倍精度浮動小数点で数値を表現することを基本としています。
浮動小数点の計算
具体的な浮動小数点の計算
いろいろな大きさの数値を2進数に変換すると、次の表の通りになります。
| 10進数 | 2進数 | 正規化した2進数 |
|---|---|---|
| $3$ | $11.0$ | $1.1\times2^1$ |
| $10$ | $1010.0$ | $1.010\times 2^3$ |
| $50$ | $110010.0$ | $1.10010\times 2^6$ |
| $100$ | $1100100.0$ | $1.100100\times 2^6$ |
| $9999$ | $10011100001111.0$ | $1.0011100001111\times 2^{13}$ |
| $0.1$ | $0.00011001100110011001100\cdots$ | $1.1001100110011001100\cdots\times 2^{-4}$ |
| $0.5$ | $0.1$ | $1\times 2^{-1}$ |
| $0.625$ | $0.101$ | $1.01\times 2^{-1}$ |
2列目が単純に10進数を2進数に変換したものになります。小数点の位置を明らかにするために、敢えて末尾を.0としています。10進数で9999程度の小さな数値でも、2進数にすると整数部分で14桁も使ってしまうことがわかります。一方、小数点以下でも桁数を多く使うものもあります。とりわけ10進数の0.1を、2進数に変換すると1100の繰り返しになり永遠に割り切れることがありません。このような制約の中で64ビットの中で効果的に数値を表現するためには、次のような正規化(Normalized floating point)という手法を採ります。
正規化の考え方
前述のように小数点を固定すると、表現できる数字の大きさや精度が限られてしまいます。そこで3列目のように、すべての数値を’1.XXX’というような形式になるよう小数点の位置を移動し、別の部分でその移動した何桁を記憶しておくようにします。小数点の位置が浮いたように移動していくので浮動小数点方式といわれる所以となっています。
ここで、50と100という整数を例に、正規化の考え方を確認します。
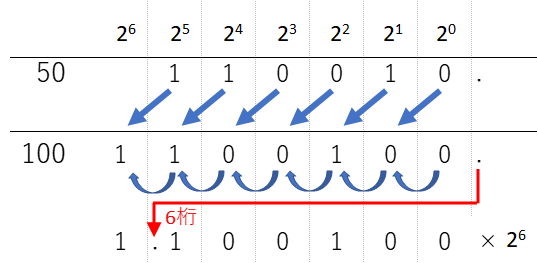
ここで50の1と0の並びを左側に1ビットだけシフト(移動)し、最後の桁に0を補います。すると、すべての項で2の乗数が1つ増え、大きさが2倍になります。ということは全体も2倍になるので$50\times2=100$になることがわかります。逆に100を右側に1ビットだけシフトすると1/2の50になります。このように、ビット全体を左にシフトすると数値そのものが2倍に、右側にシフトすると1/2倍になるわけです。
このことから、2進数で数値を表すときには、”1.XXX”となるように初めに現われる1が1の位になるようにシフトし、シフトした桁数を別の場所に覚えておくようにすれば、いろいろな大きさの数値の小数点の位置を合わせることができます。このような巧みな考え方を使い、64ビットという限られた枠の中で幅広く数値を表現しようとするわけです。
倍精度浮動小数点演算での64ビットの内訳
現在のOSでは、数値を64ビットで表現していますが、このうち、正規化された1と0の組合せを仮数部といい、53ビットが割り当てられています。また、シフトしたビット数を表す部分を指数部といい、11ビットを使用します。また、数値には正と負があるので、これを区別するために符号部として1ビット使用します。
前項で求めた100.0は次の通り表現します。
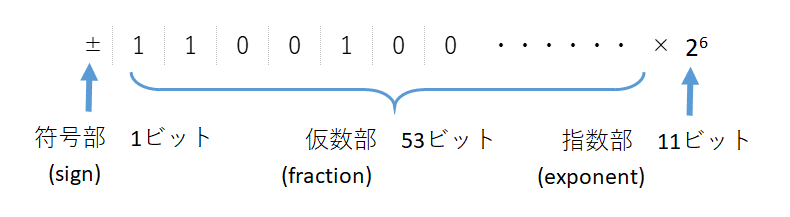
ところで図では、符号部、仮数部、指数部を合わせると65ビットとなります。64ビットから比べると1ビット多くなりますが、この秘密は次節でご紹介します。
整数を倍精度浮動小数点方式に変換するプログラム
倍精度浮動小数点方式で、整数の数値をどのように64ビットに変換するか、Pythonのプログラムを作りながら確認します。
仮数部の計算
整数を2進数に変換する
10進数で100を2進数に変換します。100は2進数に変換すると次のとおりになります。
小数を定義通り2進数に変換
- def dec2bin_int(dec):
- nary = ''
- while dec:
- nary = str(dec % 2) + nary
- dec //= 2
- return nary
- int_list = [3, 10, 50, 100, 9999]
- for i in int_list:
- print(f'{i:>4} : {dec2bin_int(i)}')
3 : 11 10 : 1010 50 : 110010 100 : 1100100 9999 : 10011100001111
dec2bin_int関数では、decで10進数の整数を渡し、変数naryで2進数を文字列として計算します。decを繰り返し2で割っていき、その都度余りをnaryに追加していきます。
3. decが0になるまで処理をくりかえすことを示します。
4. decを2で割った余りを変数naryの先頭部分に追加していきます。
5. decで2を割り、整数部分をdecとして3.に戻ります。
正規化
前述の通り、64ビットを有効に使うために、正規化します。このため、前のプログラムで求めたビットの並びを1.XXXとするためにシフトすべきビット数を計算します。
10進数を仮数部とシフトする桁数に変換する
- def dec2bin_norm_int(dec):
- nary = dec2bin_int(dec)
- frac = '1.'+nary[1:]
- expon = len(nary)-1
- return nary, frac, expon
- int_list = [3, 10, 50, 100, 9999]
- for i in int_list:
- nary, frac, expon = dec2bin_norm_int(i)
- print(f'{i:>4} : {nary:<15} : {frac:<16} : {expon:>2}')
3 : 11 : 1.1 : 1 10 : 1010 : 1.010 : 3 50 : 110010 : 1.10010 : 5 100 : 1100100 : 1.100100 : 6 9999 : 10011100001111 : 1.0011100001111 : 13
def dec2bin_norm_int関数は、前節のdec2bin_int で10進数の整数を正規化された2進数に変換した結果を使い、正規化された2進数とシフトしたビット数を計算します。
2. dec2bin_intで10進数を2進数に変換し、変数naryに代入します。
3. 変数fracで正規化した2進数を計算します。naryの初めのビットは”1”になるので、”1.”とし、naryの2ビット目以降をfracに代入します。
4. naryの長さ-1だけシフトすることになるので、この値を変数exponに代入します。
隠しビットとケチ表現(hidden ビット)
仮数部は53ビットを使い数値を表現しますが、上記のプログラムの結果を見ると正規化により必ず先頭のビットは”1”になることに気づきます。ということは、この“1”を表すために敢えて1ビット使うのは意味がないので、この1ビットを省略するようにします。このよう省略されたビットを隠しビット(hidden ビット)または、implicit MSB(most significant ビット)といい、このしくみをケチ表現(economized form)といいます。64という限られたビットを上手く配分し、少しでも仮数部で表現できる桁数を増やすとための工夫と考えることができます。このことから前の図を書き直すと次のようになります。
/
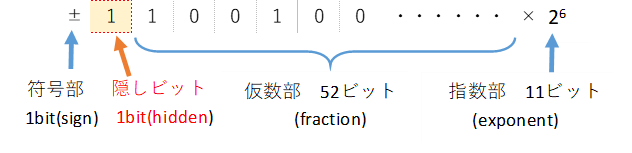
指数部の計算
指数部の計算の考え方
指数部は、仮数部を正規化するときに何ビットだけシフトしたかを表します。このとき、浮動小数点では、0.25のように1より小さい数値を扱うときには右、つまりマイナスの方向にシフトすることがあります。そこで、指数部は1023を足し合わせて計算します。この1023をバイアス値(偏り)いい、またバイアス値を使った計算方法を下駄ばき表現、オフセット・バイナリ (offset binary)といいます。具体的に次の表を見ながら確認します。

10進数で1は2進数で1となるので、仮数部も1となりシフトする必要はありません。つまりシフトするビット数は0になるので、バイアス値は1023となります。1023というのは$2^{10}-1$となるので、2進数11ビットで表現できる整数の範囲のちょうど真ん中の値になります。
次に10進数の2は2進数で”10”となり、正規化すると仮数部は1.0となり1ビットシフトする必要があります。このため、バイアス値は1024(1023+1)となります。同様に10進数の100を2進数にすると”1100100”となるので、正規化され仮数部は1.1001で6ビットシフトする必要があります。このためバイアス値は1029(1023+6)となります。
Pythonで10進数を2進数の仮数部と指数部に変換する
前節の指数部の計算を踏まえ、整数の数値を仮数部と指数部をビットとして計算するプログラムを作成します。ここでは仮数部については、割り切れた場合にも53ビットになるように”0”を補うようにします。指数部については、1023の下駄をはかせたバイアス値を2進数に変換します。
10進数を仮数部(53桁)と指数部(bias)に変換する
- def dec2bin_binary_int(dec, coef_digits=53, bias_digits=11):
- nary, frac, expon = dec2bin_norm_int(dec)
- coef = nary+(coef_digits-len(nary))*'0'
- tmp = dec2bin_int(expon+2**(bias_digits-1)-1)
- bias = (bias_digits-len(tmp))*'0'+tmp
- return coef, bias
- int_list = [3, 10, 50, 100, 9999]
- for i in int_list:
- coef, bias = dec2bin_binary_int(i)
- print(f'{i:>4}:{coef} \n\t{bias:>2}')
3:11000000000000000000000000000000000000000000000000000 10000000000 10:10100000000000000000000000000000000000000000000000000 10000000010 50:11001000000000000000000000000000000000000000000000000 10000000100 100:11001000000000000000000000000000000000000000000000000 10000000101 9999:10011100001111000000000000000000000000000000000000000 10000001100
2. base_dec2binでは10進数を2進数に変換します。
4. whileループの中で10進数を次々に2で割り、余りをnaryの右からつなげていきます。この結果naryに2進数に変換された値が文字列で代入されます。
9. ieeeでは、10進数を2進数の仮数部と指数部に変換します。
10. base_dec2binにより10進数の数値を2進数の文字列にしてnaryに代入します。
11. fracに”1.”、を代入し、それ以降2桁目以降をfracに代入します。
14. biasにはnaryの桁数-1+1023でバイアス値を計算します。
20. 1から10おきに10進数、2進数、仮数部、指数部とバイアス値とその2進数にした値を出力します。
倍精度浮動小数点の表現
これまでの結果から現在、多くのパソコンではIEEE754という基準の倍精度浮動小数点方式により、整数を64ビットの2進数に変換するプログラムを作成します。
ここで、前のプログラムに次の機能を加えます。符号部についてはプラスマイナスをあわらします。-ならば0,プラスなら1となります。
仮数部については53ビットのうち、初めのビットはケチ表現のため表示しないので、52びっとになります。
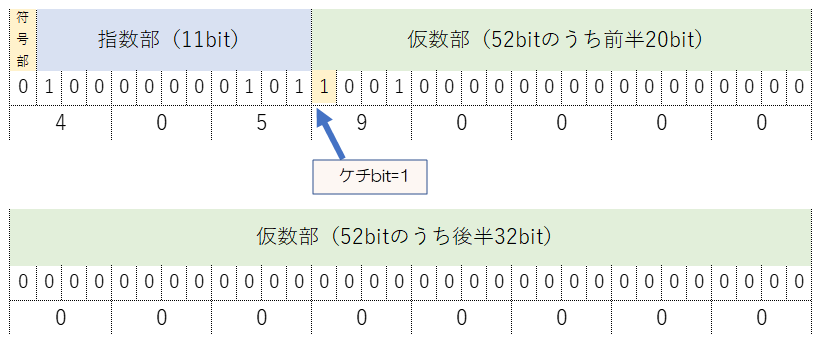
結果は2進数ではみづらいので、通常は下の行のように16進数で表します。これらは次のプログラムで出力することができます。
- def dec2bin_ieee_int(dec, coef_digits=53, bias_digits=11):
- if dec < 0:
- sign = '1'
- dec = -dec
- else:
- sign = '0'
- coef, bias = dec2bin_binary_int(dec, coef_digits, bias_digits)
- Bin = sign+bias+coef[1:]
- Hex = hex(int('0b'+Bin, 2))
- return Bin, Hex
- int_list = [3, 10, 50, 100, 9999]
- for i in int_list:
- Bin, Hex = dec2bin_ieee_int(i, 53, 11)
- print(f'{i:>5} : {Bin} \n\t{Hex}')
3 : 0100000000001000000000000000000000000000000000000000000000000000
0x4008000000000000
10 : 0100000000100100000000000000000000000000000000000000000000000000
0x4024000000000000
50 : 0100000001001001000000000000000000000000000000000000000000000000
0x4049000000000000
100 : 0100000001011001000000000000000000000000000000000000000000000000
0x4059000000000000
9999 : 0100000011000011100001111000000000000000000000000000000000000000
0x40c3878000000000