Pythonで整数部分がない小数を2進数に変換する
Pythonで小数点の計算をすると、おかしなことが起こります。極めて小さな誤差なので多くの場合は大した問題ではありませんが、やはり気になります。そこで、小数点以下の数値の取り扱いについて明らかにしていきます。
小数を2進数に変換するプログラムの考え方
浮動小数点の小数表示の問題点
0.1を単純に60桁まで表示させると、小数点第18位から555111・・・とごくわずかですが誤差が生じてしまいます。これは、Python、というよりコンピュータが2進数で数値を計算しており、そこでは浮動小数点演算が行われているためです。
0.1の小数表示
- #1 0.1の小数表示
- print(f'{0.1:.60f}')
- #0.100000000000000005551115123125782702118158340454101562500000
そこで、なぜ0.1がこのようになってしまうのか、2進数に変換して確認してみます。
小数を2進数に変換するプログラムの考え方
ここでは簡単のため、整数の部分が0である小数、例えば0.625を2進数に変換します。整数の場合には、$2^1$、$2^2\cdots$の桁に”1”が立つかを計算していきます。これに対し、小数を2進数に変換する場合、$2^{-1}=0.5$、$2^{-2}=0.25$、$2^{-3}=0.125$のそれぞれの桁に”1”が立つかどうかで計算していきます。

はじめに、0.625を$2^{-1}=0.5$で割り商(いくつ含まれているか)を求め、その値を小数点第1位とします。2進数の商は1か0なので、0.625が$2^{-1}=0.5$と比べて大きいか等しければ”1”が立つとも考えられます。小数点第1位で”1”が立つので、小数点第2位を求めるため$2^{-1}=0.5$との差、つまり0.125を計算します。
次に、0.125と$2^{-2}=0.25$との大小(商が1か?)を判断し、小数点第2位を求めます。ここでは、0.125は$2^{-2}=0.25$より小さいので”0”になります。さらに0.125を$2^{-3}=0.125$と比較すると等しくなるので(商が1)、小数点第3位は”1”になります。ここで余りは0なので、割り切れたと判断し計算は終了です。結果として、0.625は$2^{-1}=0.5$の桁と$2^{-3}=0.5$の桁が1、$2^{-2}=0.25$の桁が0となるので0.101となります。
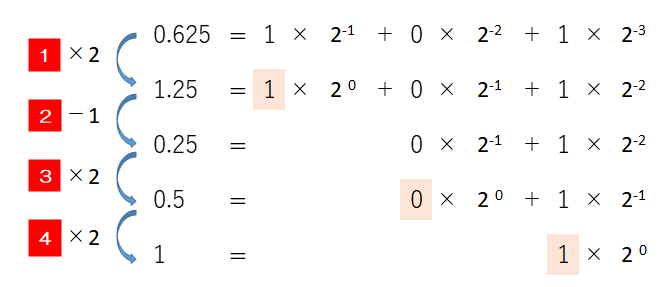
上記の考え方を踏まえ、次の流れで小数を2進数に変換するとプログラミングしやすくなります。
Pythonで整数部分がない小数を2進数に変換する
10進数の小数を単純に2進数に変換する
前節での考え方をもとに、10進数の小数を2進数に変換する関数を作成します。引数として10進数の0以下の小数と有効桁数を設定します。有効桁数(はじめに”1”が立ってからの桁数)は何も指定しないときは初期値として54桁がセットされます。54桁というのは倍精度浮動小数点の仮数部が53桁なので、割り切れなかった時に備えて1桁多くしておく必要があるためです。
10進数の小数点以下の数値を2進数に変換
- from decimal import Decimal
- def dec2bin_frac(dec,digits=54):
- dec=Decimal(str(dec))
- mantissa=''
- nth=0
- first=0
- rb=False
- while dec:
- if dec >= 1:
- mantissa += '1'
- dec = dec -1
- if first==0:
- first=nth
- else:
- if nth!=0:
- mantissa += '0'
- else:
- mantissa += '0.'
- dec*=2
- nth+=1
- if nth-first==digits:
- if dec != 0:
- rb=True
- break
- return mantissa,rb
- frac_list = [0.1, 0.5, 0.625,0.99 ]
- for i in frac_list:
- mantissa,rb=dec2bin_frac(i)
- print(f'{i:>5} : {mantissa:<60}:{rb}')
0.1 : 0.000110011001100110011001100110011001100110011001100110011 :True 0.5 : 0.1 :False 0.625 : 0.101 :False 0.99 : 0.111111010111000010100011110101110000101000111101011100 :True
3. 引数として受け取った数値は、誤差が生じないようDecimal関数を使いdecとします。
4. 2進数に変換後の値を計算するため、変数mantissaという文字列として定義します。mantissaは仮数部の意味ですが、特に小数点以下の部分というニュアンスがあります。
5. 小数点第何位を計算しているのかを把握するため、変数nthを整数型として定義します。
6. はじめに”1”になるのが何桁目かを記録しておくため、変数firstを整数型として定義しておきます。
7. digitsで指定した有効桁数だけ計算しても割り切れないときには、rbをTrueとします。このため、はじめはFalseとしておきます。
8. while文で、変数decの値を順次2倍し、値が1以上であれば1を引くという処理を0になるまで繰り返します。なお.19でdecを2倍にし、.20でいま何桁目を処理しているかを示すnthを1追加しています。
9.~13. while文の中でdecが1より大きければmantissaの末尾に”1”を追加するとともに1を差し引き、1未満であれば”0”を追加する処理を繰り返します。なお、firstが0になっているときは初めて”1”が立ったと判断し、firstにその時に処理をしている桁数nthを代入します。
14.~17. decが1より小さければ、mantissaの末尾に”0”を追加します。なお、nthが0のときには”0.”と小数点を付けます。
21. 割り切れないときは無限ループになることを防ぐため、nth-firstで初めに”1”が立ってからの桁数を計算し、この桁数がdigitsで指定した桁数になったらプログラムを終了するようにします。求めたい桁数(digits)より1桁多く計算しても割り切れないときは、round_rn関数を使い丸め処理をします
2進数の変数を正規化する
仮数部と指数部に分割する
前節の関数dec2bin_fracで、10進数の小数を計算した関数dec2bin_frac の結果を、使い仮数部の2進数のビットの並びと指数部の値を計算します。分けて変換のプログラムを変更し、正規化、つまり仮数部(mantissa)と指数部(expon)を分割します。なお、指数部は英語でexponationといいますが、ここでは省略してexponという変数にします。
10進数の小数点以下の数値を2進数に変換(正規化)
- from decimal import Decimal
- def dec2bin_norm_frac(dec,digits=54):
- mantissa,rb=dec2bin_frac(dec,digits)
- first=mantissa.find('1')
- nary=mantissa[first:]
- frac='1.'+nary[1:]
- expon=-(first-1)
- return nary,frac,expon,rb
- frac_list = [0.1, 0.5, 0.625,0.99 ]
- for i in frac_list:
- nary,frac,expon,rb = dec2bin_norm_frac(i)
- print(f'{i:>5} : {nary} \n\t{frac} : {expon}:{rb}'
0.1 : 110011001100110011001100110011001100110011001100110011 1.10011001100110011001100110011001100110011001100110011 : -4:True 0.5 : 1 1. : -1:False 0.625 : 101 1.01 : -1:False 0.99 : 111111010111000010100011110101110000101000111101011100 1.11111010111000010100011110101110000101000111101011100 : -1:True
4. “0.001xx”となっている変数mantissaからfindメソッドで1番はじめに”1”が立っている桁数を求めます。なお、findメソッドでは小数点(.)も含んでカウントしているので、firstは指数部の値より1だけ大きくなってしまいます。
5. 変数naryには、変数mantissaで初めて”1”が立ったビットから末尾までを代入します。
6. 変数fracには1.XXXになるようにして代入します。
7. 変数exponは小数では右にシフトするので、1だけ大きくなっているfirstから1を差し引き、符号をマイナスにします。
正規化された2進数をIEEE754形式に変換する
前節のdec2bin_binary_frac関数で計算した1.XXXという形式の仮数部と10進数で計算した指数部を、IEEE754形式に変換することができるよう2進数に変換します。
10進数を仮数部(coef)と指数部(expon)に変換する
- def dec2bin_binary_frac(dec,coef_digits=54,bias_digits=11):
- nary,frac, expon,rb = dec2bin_norm_frac(dec,coef_digits)
- coef=nary+(coef_digits-len(nary))*'0'
- bias=format(expon+2**(bias_digits-1)-1,'0'+str(bias_digits)+'b')
- return coef,bias,rb
- frac_list = [0.1, 0.5, 0.625,0.99 ]
- for i in frac_list:
- coef,bias,rb = dec2bin_binary_frac(i)
- print(f'{i:>5} : {coef} \n\t{bias}:{rb}')
0.1 : 110011001100110011001100110011001100110011001100110011 01111111011:True 0.5 : 100000000000000000000000000000000000000000000000000000 01111111110:False 0.625 : 101000000000000000000000000000000000000000000000000000 01111111110:False 0.99 : 111111010111000010100011110101110000101000111101011100 01111111110:True
1. 引数として仮数部の桁数(coef_digits)と指数部の桁数(bias_digits)を受け取ります。この値はさまざまな形式で計算することができるようにするためですが、倍精度浮動小数点方式を基本としているので、仮数部は53、指数部は11をデフォルトとしています。
3. 仮数部が53桁より短い場合、53桁まで"0”を補い、変数coefに代入します。なお、coefは、仮数部を表すもう一つの英語のcoefficient略です。
4. 引数で受け取った指数部の値に、下駄履きをする数値倍精度浮動小数点では2の指数部の桁数-1乗から1を引いた値($2^11-1=1023$)との和を2進数に変換する。このとき、桁数はbias_digitsとします。biasは指数部を下駄ばき表現した2進数をbiased exponentsの略です。
丸めを計算する関数
前節のプログラムで使用する丸め処理をする関数です。小数を2進数に変換するときに、倍精度浮動小数点方式では53bitを仮数部として使いますが、ここまで計算しても割り切れない場合には、最後のbitについて丸め処理をします。前節のプログラムに対し、53桁まで計算しても割り切れない場合には丸め処理をするようにします。また、0.625のように早々に割り切れた場合には、53桁目まで”0”を付け加えるように改良します。このことにより、計算結果とPythonで内部的に把握している値とを比較することができます。さらに仮数部の桁数を53桁だけではなく、自由に設定できるようにします。
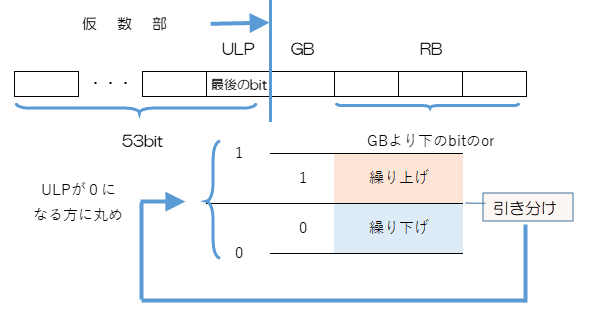
丸め処理において、仮数部(有効な桁)の最後の桁をulp(Unit in the Last Place)といいます。また、その次のbitをgb(Guard bit)といい、さらにそれ以下のbitのうち1つでも”1”が立てば”1”になるようなbitをrb(Round bit)といいます。実際に計算するときはgbまで計算し、ここで割り切れればrb=”0”、割り切れなければrb=”1”とします。
丸め処理ではgbとrbを組み合わせ、その数値が切り上げた値と切り捨てた値のどちらに近いかで判断します。まず、gb=”1”、rb=”1” のときには切り上げた値に近いと考えます。ところが、rb=”0”、つまりgbの桁で割り切れたときには引き分け(どちらとも同じ近さ)となります。ここで常に切り上げるなどと決めてしまうと、全体として数値が大きい方に偏ってしまいます。そこで、ulpが”1”のときには切り上げ、ulpが”0”のときには切り捨てとして、uplが”0”になるように丸めます。これは、10進数で最後の桁が偶数になるように丸めるのと同じで、2進数の場合も、最後の桁がなるべく0になるようにしていると考えられます。一方、gb=”0”の場合は切り捨てた値に近づくので、無条件に切り捨てとなります。これらを表にすると、次の通りです。
| ulp | gb | rb | 結果 |
|---|---|---|---|
| 0 | 0 | 0 | 切り捨て |
| 0 | 0 | 1 | 切り捨て |
| 0 | 1 | 0 | 切り捨て |
| 0 | 1 | 1 | 切り上げ |
| 1 | 0 | 0 | 切り捨て |
| 1 | 0 | 1 | 切り捨て |
| 1 | 1 | 0 | 切り上げ |
| 1 | 1 | 1 | 切り上げ |
2進数の丸め処理をする
- def round_bin(nary,rb):
- ulp=nary[-2] #unit in the last place
- gb =nary[-1] #Guard bit
- sw_up= False
- if gb=='1':
- if rb==True: #Round bit
- sw_up=True
- else:
- if ulp=='1':
- sw_up=True
- result=nary[:-1]
- if sw_up==True:
- return bin(eval('0b'+result) +eval('0b'+(len(nary)-2)*'0'+'1'))[2:]
- else:
- return result
- print(round_bin('110',True))
- print(round_bin('111',True))
- print(round_bin('111',False))
- print(round_bin('101',False))
- print(round_bin('110',False))
- print(round_bin('100',False))
11 100 100 10 11 10
1. 引数naryで仮数部+gb(求めたいbitより1桁だけ多く)までの2進数を文字列として、またgbまで計算して割り切れなかった場合には、rb=Trueとして受け取ります。
4. sw_upはいったんFlaseで定義し、切り上げると判断したときにはTrueを代入するようにします。このため、gb=”0”の場合のように、切り上げの条件にあてはまらなければ自動的に切り捨てられるようになります。
5. gb=”1”のとき、rb=Trueであれば1つ繰り上がるので、sw_up=Trueとします。
8. gb=”1”でrb=Falseのときは、ulp=”0”になるように丸めるため、ulp=”1”の場合に切り上げるようにします。
11. resultにはnaryからgbを取り除いた値が代入されます。したがって切り捨てられるときには、この値が戻り値になります。
12. 切り上げられる場合は、resultを2進数に変換した数値と、仮数部で最小の値(000・・・01)を2進数に変換した数値の和を計算します。この値が切り上げられるときの戻り値になります。
IEEE754形式の倍精度浮動小数点型に変換
これまで作成した関数を使い、整数部分が無い小数をIEEE754形式の浮動小数点型に変換します。ここでは、マイナスの場合の対応と、指定した桁数で割り切れない場合の丸め処理をし、最終的には64桁の2進数と、これを見やすくするため16進数に変換した値を返します。
IEEE754形式に変換する
- def dec2bin_ieee_frac(dec,coef_digits=53,bias_digits=11):
- if dec < 0:
- sign = '1'
- dec = -dec
- else:
- sign = '0'
- coef_prev, bias ,rb= dec2bin_binary_frac(dec,coef_digits+1,bias_digits)
- if rb==True:
- coef=round_bin(coef_prev,rb)
- else:
- coef=coef_prev[:-1]
- Bin = sign+bias+coef[1:]
- Hex = hex(int('0b'+Bin, 2))
- return Bin, Hex
- frac_list = [0.1, 0.5, 0.625,0.99 ]
- for i in frac_list:
- Bin,Hex = dec2bin_ieee_frac(i)
- print(f'{i:>5} : {Bin},\n\t{Hex}')
0.1 : 0011111110111001100110011001100110011001100110011001100110011010, 0x3fb999999999999a 0.5 : 0011111111100000000000000000000000000000000000000000000000000000, 0x3fe0000000000000 0.625 : 0011111111100100000000000000000000000000000000000000000000000000, 0x3fe4000000000000 0.99 : 0011111111101111101011100001010001111010111000010100011110101110, 0x3fefae147ae147ae