Pythonによる整数の桁に関する計算

ある整数が3の倍数であるかを調べるのに、各桁の数字を合計した値が3で割り切れるかで判断することができます。例えば471の場合4+7+1=12となり3で割り切れるので、471は3の倍数です。このように整数を桁ごとに分割するような計算をPythonで行います。

整数の各桁とリストを交互に変換する

整数を桁ごとに分割する

3桁の数字を100の位と10の位と1の位に分割する

3桁の整数を、余りと割り算を使って桁ごとに分割します。

dig_1

1の位の数

dig_10

10の位の数

dig_100

100の位の数

3桁の整数を桁ごとに分割する

1. num=471
2. dig_1=num%10
3. num//=10
4. dig_10=num%10
5. num//=10
6. dig_100=num%10
7. print(dig_100)
8. print(dig_10)
9. print(dig_1)

4
7
1

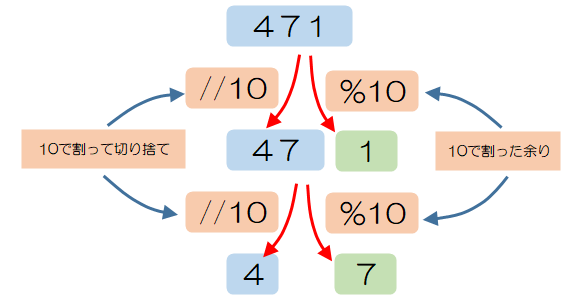
2. 分割したい整数numを10で割って余りを計算することで、1の位を取り出すことができます。この値をdig_1に代入します。

3. 残りの100の位と10の位を分解するために、numを10で割って小数点以下を切り捨て、2桁の整数としてnumを置き換えます。

5.6. 2.3と同じ処理を繰り返すことでdig_100に100の位、dig_10に10の位の数字を代入することができます。

整数の各桁とリストを交互に変換する

整数の各桁を分解してリストにする関数を作成します。この関数を使うと各桁の合計を計算したり大きい順番に並び替えたりすることが、簡単にできるようになります。

整数の各桁をリストに変換する

整数の演算をするため、各桁をリストに変換します。

整数の各桁をリストに変換する

1. def num2lst(num):
2. digits_l = []
3. while True:
4. digits_l.insert(0,num % 10)
5. num //= 10
6. if num == 0:
7. return digits_l
8. num2lst(471)

[4, 7, 1]

4　numで受け取った整数に対し4.において10で割った余りを計算することで、1の位の値を取り出すことができます。この数値は、リストdigits_lに挿入しますが、10の位、100の位と桁が左に行くにしたがって、常にリストの先頭（左方向）に挿入する必要があるので、insertメソッドで、挿入位置を0とします。

5.　末尾の桁を抜き出すことができたら、次の取り出すためｍumを10で割って切り捨てておきます。

6.7. numが0になった時点で全ての桁を取り出したことになるので、リストを返り値として関数を抜けます。

整数を桁ごとに要素とリストを整数に変換する

桁ごとの値を要素とするリスト（digits_l）を整数に戻す関数を作成します。

桁ごとの値を要素とするリストの作成

1. def lst2num(digits_l):
2. num = 0
3. for i in digits_l:
4. num = num * 10 + i
5. return num
7. lst2num([4,7,1])

471

3.　 for文で要素iを順次取り出すと、桁数が大きな順に整数が取り出されます。

4.　1回目のループではiがnumに代入するだけですが、2回目以降はnumを10倍しiを加えていきます。このことにより、値の大きな桁が次々と10倍されていきます。

整数が3で割り切れるか判定する

%演算子を使うことにより、整数をある数で割った余りを計算することができますが、ここでは筆算でもできる方法で判定することを考えます。

3で割り切れるか判断

1. num=123456789
2. d_lst=num2lst(num)
3. total=sum(d_lst)
4. print(total,total%3)

45 0

num2lst関数で、numをリストに変換できるので、sum関数で各桁の合計を計算することができます。123456789の各桁の合計は45になり、いずれも3で割り切れることがわかります。

任意の桁ごとに区切ってリストに変換する

3桁ごとに区切ってリストにする

前節では、整数を1桁ごとに区切ってリストにしましたが、1の位から数えて任意の桁ごとに区切ってリストにする関数を作成します。

整数を3桁ごとに区切る

1. def num2lst_n(num,digits=1):
2. digits_l = []
3. while True:
4. digits_l.insert(0,num % 10**digits)
5. num //= 10**digits
6. if num == 0:
7. return digits_l
9. print(num2lst_n(2354471,3))
10. print(num2lst_n(2354471))

[2, 354, 471]
[2, 3, 5, 4, 4, 7, 1]

1.　引数には対象となる正の整数numと、区切りの単位となる桁数digitsを指定します。digitsを指定しないときは1となるように初期値を与えています。

4.　対象となる整数を割って余りを求めるとき、10のdigits乗にすることで、digitsで指定する桁数ごとに区切ってリストに挿入することができます。

5.　次の区切りの計算をするため、10にdigitsを乗じた数値で割って小数点以下を切り捨てます。

9.　2354471を3桁区切りにリスト化しています。一番上位の100万の桁は1桁となります。

10. 引数digitsを指定しないと、1桁区切りのリストにします。

7の倍数であるかを判定する

ある整数が７の倍数かどうかを判断するときは、3桁ごとに区切って計算した結果を使います。1の位の桁から3桁ごとに区切り、区切りごとに交互にプラス、マイナスをして足しこんでいった値が7の倍数であるときは、元の整数は7の倍数と判断されます。

例えば、2354471の場合、2、354、471のように分け、2-354+471=119となります。119は7の倍数なので2354471も7の倍数になります。

7で割った余りを計算

1. def mod_7(num):
2. d_l=num2lst_n(num,3)
3. total=0
4. for i,item in enumerate(d_l):
5. total+=(-1)**i * item
6. return abs(total)
8. for i in range(7):
9. print(i,mod_7(7*336353+i)%7)

0 0
1 1
2 2
3 3
4 4
5 5
6 6

2.　num2lst_n関数で3桁ごとに区切り、リストd_lに挿入します。

4.　3桁ごとに区切ったリストの要素に対し、enumerate関数を要素の順番iと値itemを取り出します。

5　要素をプラス、マイナス交互に足しこむため、-1をi乗じた値を掛けます。

9.　336353×7＝2354471は7の倍数になるので、これに０から6までを加えた数値にmod_7関数を適用すると、戻り値を7で割った余りは、元の余りと一致します。

文字列

数字を文字列に変換して扱う方が簡単な場合もあります。ここでは、さまざま型同士の変換を確認します。

整数を文字型に変換する

整数を文字型に変換

1. intX=43601
2. strX=str(intX)
3. print(strX[0])
4. print(strX[-1])
5. print(strX[1:2])
6. print(strX[2:])

4
1
3
60

2　intXに整数43601を代入し、str関数で文字列に変換します。

3.～6. 文字列に変換するとインデックスで任意の桁を取り出すことができます。

文字列、リスト、整数間の変換

文字列をリストに変換する

list関数を使うと文字列を1文字ずつに分解し、リストに変換することができます。

文字型をリストに変換

1. strA='43601'
2. lstA=list(strA)
3. print(lstA)

['4', '3', '6', '0', '1']

2.　文字列に対しリスト関数を適用すると、リストに変換することができます。ただし、strAにように全て数字である要素に対しても変換後のリストの要素は文字列になるのでそのままでは計算に使えません。

文字列を並べ替えてリストに変換

文字列にsorted関数を適用すると1文字ずつに分解し、並び替えたのち、リストに変換することができます。

文字型をリストに変換

1. strB='43601'
2. lstB=sorted(strB)
3. print(lstB)
4. lstBr=sorted(strB,reverse=True)
5. print(lstBr)

['0', '1', '3', '4', '6']
['6', '4', '3', '1', '0']

2.　単純にsorted関数を適用すると、昇順（小さい順）に並び替えられます。

4.　sorted関数で、reverse=Trueと指定すると、降順(大きい順)に並び替えられます。

リストを文字列に変換する

文字列に、リストの中身を引数としてjoinメソッドを適用すると、リストを文字列に変換することができます。

リストを文字型に変換

1. lstC=['4','3','6','0','1']
2. strC=''.join(lstC)
3. print(strC)
4. strC=','.join(lstC)
5. print(strC)

43601
4,3,6,0,1

2.　適用する文字列をブランクにすると、単純にリストの各要素が文字列に結合されます。

4.　文字列に指定した内容を区切りとして、新たに文字列が作成されます。

区切りのある文字列をリストに変換

区切りのある文字列をリストに変換

1. strD='4 3 6 0 1'
2. lstD=strD.split()
3. print(lstD)

['4', '3', '6', '0', '1']

カンマで区切った文字列をリストに変換

カンマで区切った文字列をリストに変換

1. strE='4,3,6,0,1'
2. lstE=strE.split(',')
3. print(lstE)

['4', '3', '6', '0', '1']

整数のリストを文字列のリストに変換する

整数型を要素としているリストを一括して文字列を要素とするリストに変換します。このときにはmap関数を使用します。さらに、リストをカンマで区切った文字列に変換するためにはjionメソッドを適用します。

整数のリストを文字列のリストに変換

1. lstFi = [4, 3, 6, 0 ,1]
2. lstFs =list(map(str, lstFi))
3. print(lstFs)
4. strFs=','.join(map(str, lstFi))
5. print(strFs)

['4', '3', '6', '0', '1']
4,3,6,0,1

整数を特定の桁数の文字列に変換する

5桁の整数として扱っているが、たまたま計算結果が3桁になってしまうことがあります。このとき、強引に上の桁か下の桁に0を2桁付け足して5桁の数字として扱いたい場合があります。このときには、文字列にljustメソッド、rjustメソッドを適用します。

文字列を数値型に変換するにあたり０を補う

1. x='123'
2. xl= x.ljust(5,'0')
3. xr= x.rjust(5,'0')
4. print(xl,xr)

12300,00123

2.　3桁の文字列にljustメソッドで桁数と文字列を指定すると、指定した桁数になるまで文字列（ここでは’0’）を右側に補います。

3.　 3桁の文字列にrjustメソッドで桁数と文字列を指定すると、指定した桁数になるまで文字列（ここでは’0’）を左側に補います。

カプレカ数の計算

カプレカ数とは

カプレカ数は、3桁の整数を考える場合、次のような不思議なことがおこります。

1.　3桁の整数を、大きい順番に並べ替えた数から小さい順に並べ替えた数を引き算します。例：381→831-138=693

2.　1.の計算を繰り返します。

例：693→963-369=594→954-459=495

3.　元の数が555のように3つとも同じでなければ、6回以内の計算で495に落ち着きます。この495のような数字を3桁の整数のカプレカ数といいます。なお、3桁とも同じ場合の計算結果は0になります。

なお、カプレカ数は3桁以外の整数についても存在します。

カプレカ数の計算で最大値から最小値の差を計算する関数

桁数を並べ替える

1. def differ(num):
2. min=sorted(str(num).rjust(3,'0'))
3. max=sorted(str(num).rjust(3,'0'), reverse=True)
4. return int(''.join(max))-int(''.join(min))
6. print(differ(381))
7. print(differ(693))
8. print(differ(594))

693
594
495

カプレカ数の計算

1. for i in range(100,1000):
2. Kaprekar=i
3. cnt=0
5. while Kaprekar!= 495 and Kaprekar!= 0:
6. cnt+=1
7. Kaprekar=differ(Kaprekar)
8. print(i,Kaprekar,cnt)

100 495 6
101 495 6
102 495 5
103 495 4
104 495 3
105 495 1
106 495 2
（以下略）