Pythonで計算することができる数の大きさ

Pythonで整数の取り扱いについて、知っておきたいことをご紹介します。

整数型と小数型の違い

数字におけるデータの型

Pythonで割り算をすると

Pythonで割り算をすると次のようになります。

#1 Pythonによる割り算の結果
x=4
y=2
print(x//y)
print(x%y)
print(x/y)
print(type(x%y))
print(type(x/y))

2
0
2.0
＜class 'int’＞
＜class 'float'＞

割り算での商（小数点以下を切り捨てる計算）は”//”で余りは”%”を使い求めることができます。このとき答えが必ず整数になるので2，0のように表示されますが、単純に割り算をするときには、割り切れたとしても強制的に2.0と小数表示になります。この違いを見るためtype関数を使い、計算結果の型を見ると、2はint(整数：integerの略)、2.0はfloat（小数）となります。

自動的に定義される型

ここでみてきた型について、もう少し詳しく見ます。

#2 Pythonによる型の定義
x=2
y=2.0
print(type(x),type(y))
x=2.0
y=2
print(type(x),type(y))

＜class 'int'＞ ＜class 'float'＞
＜class 'float'＞ ＜class 'int'＞

多くのプログラミング言語では、変数を使う前には名前とともに、どのような型（整数や小数など）かを定義します。しかしPythonでは定義することなく、変数の名前を決め、値を代入するだけで使えるようになります。

同じ大きさの数字を代入する際にも、xのように2を代入すると整数となり、2.0を代入すると少数になります。しかも、同じプログラムの中で、値を代入すると変数の型は入れ替わります。

多くの場合、その違いは意識しなくても問題にはなりませんが、無頓着でいると足元をすくわれかねないので、細かいところをみてみます。

Pythonで取り扱うことのできる整数の最大値

小数型での大きな数の計算

データの型が整数か小数かの違いで問題になるのは、大きな数字を取り扱うときです。データの型が小数の場合、Pythonで正確に計算することができる整数の最大値は$2^{53}=9007199254740992$になります。

#3 少数で正しく計算することができる数字の範囲
x=2**53
print(x)
print(x+1.0)
print(x-1.0)
print(x+2.0)
print(x+3.0)
print(x+4.0)

9007199254740992
9007199254740992.0
9007199254740991.0
9007199254740994.0
9007199254740996.0
9007199254740996.0

例えばこの数値に1.0を足すと、型は小数となり9007199254740993.0にもならず、さりとてエラーになることもなく9007199254740992.0となります。さらに$2^{53}$に同様に2.0、3.0、4.0を足していくと1の位が偶数になってしまい、しかも不規則に増加していきます。これに対して1.0を引くときには同じ小数型にもかかわらず正しく計算されます。このように少数の場合は9007199254740993より大きな数値も計算することはできますが、誤差が発生してしまいます。$2^{53}$は約9000兆なので、多くの場合には問題になりませんが、整数を数学的に扱う場合にはうまくいかなくなる恐れがあります。

整数型での大きな数の計算

Pythonでは整数型にすると、$2^{53}$を超える整数であっても正確に表示、計算することができます。

#4 整数で正しく計算することができる数字の範囲
x=2**53
print(x+1)
print(x+2)
print(x+3)
print(x+4)

9007199254740993
9007199254740994
9007199254740995
9007199254740996

このように、整数型の場合には$2^{53}$を超えても正確に計算することができます。結論として、整数型であればコンピュータの性能が許せばどんなに大きな数字でも計算することができます。

大きな数の計算の実例

次のような計算も、整数型ということでPythonは正確に計算します。

# 5 Pythonでは整数型ではどんなに
print(1111 * 1111)
print(11111 * 11111)
print(111111 * 111111)
print(1111111 * 1111111)
print(11111111 * 11111111)
print(111111111 * 111111111)
print(1111111111 * 1111111111)
print(11111111111 * 11111111111)
print(111111111111 * 111111111111)
print(111111111111 * 111111111111*2)

1234321
123454321
12345654321
1234567654321
123456787654321
12345678987654321
1234567900987654321
123456790120987654321
12345679012320987654321
24691358024641975308642

最後の行は123垓というとんでもなく大きな数字になります。ちなみに10,000兆が京（けい）、10,000京が垓となります。

IPアドレス

インターネットに接続された機器の住所を示すような仕組みをIPv6といわれており、この中でIPアドレスという番号を付けています。この番号は128ビットつまり、$2^{128}$通りの番号を扱うことができます。このことから、理論的に何台の機器を接続することができるか考えています。

#6 IPv6で表すことができるIpアドレスの数
print(2**128)
print(2**128+1)

340282366920938463463374607431768211456
340282366920938463463374607431768211457

このようにとんでもない$340×10^{38}$桁というとんでもない数になります。これは340澗2823溝6692穣0938予4634垓6337京4607兆4317億6821万1456という途方もない数字となります。さらにこの数に1を足しても正しく計算してくれます。

大きな数字を少しだけわかりやすく入力する方法

大きな数字を入力するときには桁区切りができると便利です。このときには”,”ではなく”_”を使って区切ります。

#7 大きな桁数の表示
print(340_282_366_920_938_463_463_374_607_431_768_211_456)
print(340_282_366_920_938_463_463_374_607_431_768_211_456*2)

340282366920938463463374607431768211456
680564733841876926926749214863536422912

Excelのように”,”が付けられないので少し違和感がありますが、計算もしっかりしてくれます。

マイクロソフトエクセルの場合

それでは我々がいつもお世話になっているエクセルではどうでしょうか？

マイクロソフトのホームページによると、有効桁数は10の15乗と書かれています。

セルA1に14桁で1番大きな数字999兆9999億9999万9999－1を入力し、列幅を広げた上で整数表示にします。これに対し、数字を1ずつ足し算していくと、おかしなことが起こります。

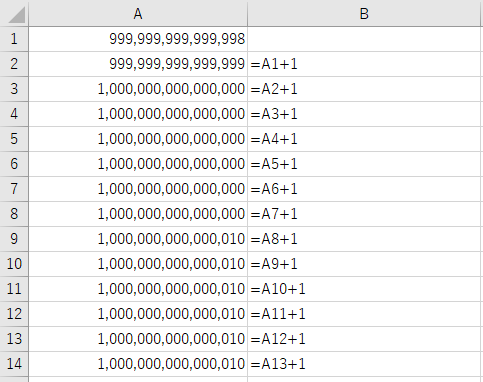
セルA3の1000兆ぴったりまでは良いのですが、それに1を加えても1000兆とおなじ数字が表示されます。そして1000兆6になった時点で1000兆10となり、整数部分を勝手に四捨五入してしまいます。（細かいことをいうと下1桁が5のときは切り下がっているので、JIS丸めによっているものと思います。）おそらく我が国の事務処理の分野で1000兆円を超える数字を扱うのは、財務省で国債の残高を管理している部門くらいだと思います。このような意味ではエクセルでも十分のような気がしますが、次のような計算をすると、下1桁は一目で1と分かるのに、計算結果の下1桁は0と明らかにおかしなことになります。

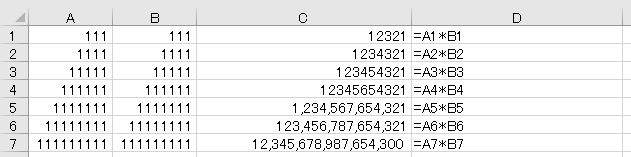
まとめ

Pythonの小数とエクセルについては、かなり大きな数字になると計算はできるものの細かいところで誤差が生じてしまいます。つぎからこのからくりを調べてみます。