Pythonによる約数の計算と素因数分解

Pythonによる約数の計算

約数をリストで求める関数

約数を単純に出力する

pythonで約数を求めるプログラムで、もっとも単純なものを作成します。ここでは正の整数36の約数を1から36までの整数で割って、余りが0の場合に約数として出力します。

約数を列記する
num
約数を求める対象の正の整数、ここでは36を代入
i
numの約数であるかを判断するため、1から36まで順次代入
  1. num = 36
  2. for i in range(1, num+1):
  3. if num % i == 0:
  4. print(i, end=" ")

1 2 3 4 6 9 12 18 36

2.　numを割られる数として、1からnumまでの正の整数iで順次、割っていきます。range(num)とすると、0からnum-1=35までの範囲で計算されてしまうので、range(1, num +1)とします。
3.～4. 割り算の結果、余りが0のときは、iを約数として出力します。print(i)とすると結果が縦に表示されてしまうので、引数としてend=” ”を指定して、横に並べて表示するようにします。

約数をリストで出力する

計算した約数の一覧をリストにしておくと、約数の個数や合計をする場合など、次のステップで活用することができます。

約数のリストを作成する
  1. num = 36
  2. divisors = []
  3. for i in range(1, num+1):
  4. if num % i == 0:
  5. divisors.append(i)
  6. print(divisors)

[1, 2, 3, 4, 6, 9, 12, 18, 36]
2.～5. divisorsというリストを空の状態（[]）で定義し、forループの中で約数が見つかったら5.でdivisorsに約数として追加します。

約数をリストで求める関数

いろいろな数値に対する約数を計算するプログラムを作る場合、関数にしておくと便利です。

約数をリストで返す関数
  1. def divisors_list(num):
  2. divisors = []
  3. for i in range(1, num+1):
  4. if num % i == 0:
  5. divisors.append(i)
  6. return divisors
  8. divisors_list(36)

[1, 2, 3, 4, 6, 9, 12, 18, 36]
9.　divisors_list関数に引数numとして36を渡すと、約数をリストとして返します。

リスト内包表記やラムダ式による約数の計算

リスト内包表記

リスト内包表記で約数を計算することができます。リスト内包表記は処理速度が速いといわれています。

リスト内包表記で約数を求める
  1. num = 36
  2. [i for i in range(1, num+1) if num % i == 0]

ラムダ式

ラムダ式でも約数を計算することができます。

ラムダ式で約数を求める
  1. num = 36
  2. list(filter(lambda i: num % i == 0, list(range(1, num+1))))

いずれも、前と同じく[1, 2, 3, 4, 6, 9, 12, 18, 36]となります。

効率的な約数の計算

前節では約数の計算をするために、正の整数numに対して、1からnumまでの数字をiに順次代入し、割り切れる(num%i==0)場合にiを約数と判断しました。36のような小さな数であれば問題はありませんが、大きな数の約数を計算する場合、計算量が膨大になり時間がかかってしまいます。そこで、少しでも計算量を減らすことを考えます。

約数は対象となる数の半分まで調べれば計算可能

36の約数は次のとおり分類されます。

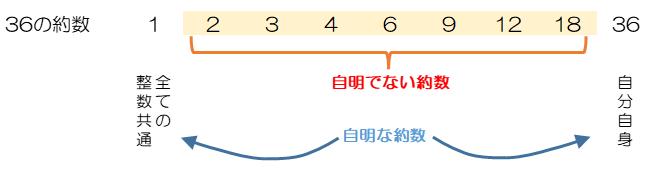
自明の約数
自明の約数

(A) 1（すべての正の整数で共通）

(B) 素数でなければそれ以外の約数

(C) 自分自身（num）

(A)と(C)は言うまでもないので、自明の約数（trivial divisor）といいます。(A)は全ての正の整数で共通なのではじめからリストに入れておきます。(C)は最後にnumをリストに挿入すればよいので、自明でない約数（non-trivial divisor）をfor文で見つければよいことになります。

約数を計算する関数のループを減らして効率化
  1. def divisors_list_h(num):
  2. divisors = [1]
  3. if num == 1:
  4. return divisors
  5. for i in range(2, num//2+1):
  6. if num % i == 0:
  7. divisors.append(i)
  8. divisors.append(num)
  9. return divisors
  11. print(divisors_list_h(1))
  12. print(divisors_list_h(36))

2.　(A)の1はすべての正の整数の約数になるので、リストを定義するときに予めセットしておきます。
5.～7. (B)のfor文では、自明でない約数で一番小さい2から、numをその2で割って切り捨てた値までループさせることで足ります。
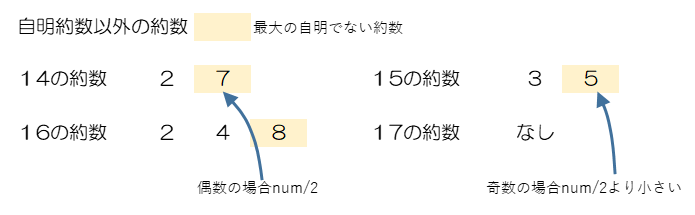
自明の約数
自明の約数
図のようにnumが偶数であれば2が約数になり、自明でない約数の最大値はnum/2になります。numが奇数の場合、自明でない約数の最小値は3以上になるので、自明でない約数のうち最大のものはnum/3（15であれば5）になります。結果として、num/2まで計算すれば漏れがなくなります。このためrange(2, num/2)としたいところですが、range関数は整数しか引数とすることができず、range関数の「まで」の部分は+1する必要があるので、range(2, num//2+1)とします。ちなみにnum//2は2で割って小数点以下を切り捨てた値を返します。
8.　(B)の処理が終わったら、(C)のnumも必ず約数になるので8行目でリストに追加します。

なお、numが1のときには、（A）と(C)がともに1なので、計算結果が[1,1]となってしまいます。このことを防ぐために、2.でnumが1であれば何も処理せず関数の処理を終了します。

計算範囲を対象となる数の平方根までにする

正の整数36を例にとると約数の1つは2であり、36をこの2で割った18もまた36の約数になります。このように、約数を(1,36)、(2,18) 、(3,12) 、(4,9)、(6,6)と積が自分自身36になるようなペアをつくることができます。そこで、約数が1つ計算できたら、同時にペアの約数もリストに追加することにより計算量を減らすことを考えます。

#7 約数を返す関数の相手方も同時に計算することで効率化
  1. def divisor_list_s(num):
  2. divisors = []
  3. for i in range(1, int(num**0.5)+1):
  4. if num % i == 0:
  5. divisors.append(i)
  6. if i**2 == num:
  7. continue
  8. divisors.append(int(num/i))
  9. # return divisors # 昇順にしなくてよいならソートは不要
  10. return sorted(divisors) # 昇順にしたいときはソートする
  12. divisor_list_s(36)
4.　約数が見つかると、5.で約数をリストに追加するとともに、8行目でペアの相手方もリストに追加します。例えば約数2が見つかると18もリストに追加します。
6.7. 36（=6×6）のように重解であるときは、6が重複して追加されることを防ぎます。continue文により、iを1つ増やして次の約数を探します。
9. 10. divisorsを返すと、[1, 36, 2, 18, 3, 12, 4, 9, 6]のように小さな順番に並びません。昇順に並び替えるようにしたい場合は、return sorted(divisors)とします。

3.でfor i in range(1, int(num**0.5)+1)としているのは次の理由です。

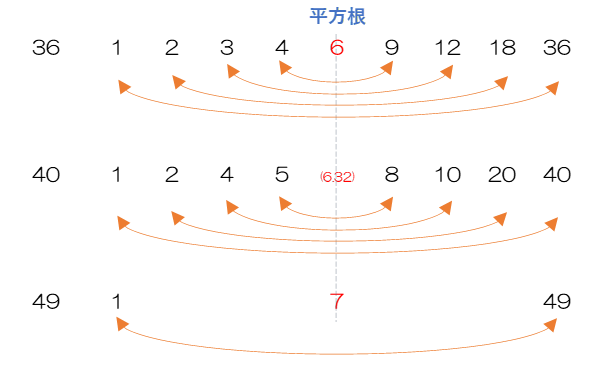
約数のペアの計算
約数のペアの計算

numの平方根がピッタリと整数にならないときは、切り捨てても問題ありません。たとえばnum=40の場合、平方根は約6.32となり、約数のペアのうち小さい方の数は6より大きくなることはありません。また、range関数の特性から+1まで指定する必要があります。

#6と#7を比べると、numが小さいうちは問題ありませんが、num=10,000となると、#6では5,000回ループする必要がありますが、#7では100回で済み効率的です。

素因数分解をする

素因数分解をするプログラムを作成します。例えばnum=24を素因数分解すると、$24=2\times2\times2\times3$のように単純に素因数をリストとして列記する方法が考えられますが、通常は$24=2^3\times3$のように素因数とその乗数で表すのが一般的です。そこで、これを辞書形式で出力することを考えます。以下では、素因数分解を次の変数を使って計算します。

prime
素因数を表します。24の場合、$24=2^3\times3$の2と3を表します。
expon
べき乗を表します。素因数2に対する3乗、3に対する1乗の部分を表します。

素因数分解の考え方

素因数分解は約数とは異なり、素因数をみつけると、その商がさらにその素因数で割り切ることができるか調べる必要があります。24の素因数分解の場合、素因数2を見付けると、商は12、さらに6，4，2とその素因数2で割り続ける必要があります。

# 8 素因数分解の結果をリストで列記する関数
  1. def prime_f_list(num):
  2. divisors = []
  3. for prime in range(2, num+1):
  4. while (num % prime) == 0:
  5. divisors.append(prime)
  6. num //= prime
  7. return divisors
  9. print(prime_f_list(7776))

[2, 2, 2, 2, 2, 3, 3, 3, 3, 3]

3.～6. for文で、primeを素因数の候補としてnumを割り切ることができるか順次調べていきます。
4.～6.文でnumをprimeで割って余りが0となり素因数であることがわかると、primeをリストdivisorsに追加します。同時に素因数分解の対象はnumをprimeで割った値となるので、この値でnumを置き換えます。さらにnumがprimeで割り切れなくなるまで、while文で繰り返し同じ処理をします。
7.　num(＋1)まで約数であるかを調べたらfor文を抜けて、素因数分解をした結果をとリストdivisorsを返します。

素因数分解の結果を見やすくする

素因数分解はのように、べき乗を使って表現するのが一般的です。そこで、辞書形式で素因数分解をするプログラムを作成します。

#9 素因数分解の結果を辞書形式で求める関数
  1. def prime_f_multi(num):
  2. divisors = {}
  3. for prime in range(2, num + 1):
  4. expon = 0
  5. while (num % prime) == 0:
  6. expon += 1
  7. num //= prime
  8. if expon != 0:
  9. divisors[prime] = expon
  10. return divisors
  12. print(prime_f_multi(24))
  13. print(prime_f_multi(7776))

{2: 3, 3: 1}
{2: 5, 3: 5}
3.～9. for文で、primeを素因数の候補としてnumを割り切ることができるか順次調べていきます。
5.～7. while文で、numを割り切るprimeが見つかったら、primeに対するexponを1だけ増やし、numをprimeで割った値に置き換えます。さらにnumがprimeで割り切れなくなるまで、while文で繰り返し同じ処理をします。
8.　while文を抜けたら、辞書devisorsにkeyに素因数prime、valueにべき乗exponを追加します。
12. $24=2^3×3$であることがわかります。
13. $7776=2^5×3^5$のように計算されますが、このように大きな値になるとこの方法はあまり効率的ではありません。例えばnum=7776を引数とした場合、素因数prime=2が見つかり、3888、1944と小さくなりその中で素因数を見付ければすむものを、for文ははじめに命令した通り、prime=7776までループしてしまうためです。そこで、次節ではwhile文を使ってこの問題を解決します。

for文をwhile文に置き換えて効率化する

ここではwhile文を使い、プログラムを効率化します。

#10 素因数分解を辞書形式で求める関数を効率化
  1. def prime_f_dict(num):
  2. divisors={}
  3. prime=2
  4. while(prime <= num):
  5. expon=0
  6. while(num % prime == 0):
  7. expon+=1
  8. num //= prime
  9. if expon != 0:
  10. divisors[prime]=expon
  11. prime += 1
  12. return divisors
  14. print(prime_f_multi(24))
  15. print(prime_f_multi(7776))

{2: 3, 3: 1}
{2: 5, 3: 5}

3　while文を使うために、素因数の候補primeに2を代入し、順次、それより大きな数につき素因数であるか調べていきます。
4.　前節ではfor文で素因数の候補primeをnumまでループさせましたが、かわりにnumがprimeより大きい間はループするように変更します。primeがnumより大きくなれば、それ以降は素因数になることはありえないため、ここまでですべての素因数を見つけ出すことができます。
11. ある素因数primeでの処理が終わったらこれに1を加え、より大きな素因数を探します。

素因数分解の素因数を見付けるために、for文でもwhile文でも同じ結果を得ることができます。for文は約数の候補をコントロールするカウンタ（ここではprime）を順次追加することをしなくてすむ分、効率が悪くなることがあります。一方、while文はカウンタを増やすような処理を入れる必要がある分、細かな調整をし、効率を上げることができることがあります。

sympyモジュールによる約数の計算

sympyモジュールを使うと、約数の計算を簡単にすることができます。

sympyモジュールで約数や素因数を求める関数

Sympyモジュールで約数をリストとして求める

Sympyモジュールのdivisors関数で素因数分解をすることができます。

#11 sympyにより約数、約数の個数を計算
  1. import sympy
  2. print(sympy.divisors(7776))

[1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, 48, 54, 72, 81, 96, 108, 144, 162, 216, 243, 288, 324, 432, 486, 648, 864, 972, 1296, 1944, 2592, 3888, 7776]

Sympyモジュールで素因数分解する

Sympyモジュールのfactorint関数で素因数分解をすることができます。

#12 sympyにより素因数分解
  1. print(sympy.factorint(7776))

{2: 5, 3: 5}

sympyモジュールの関数と比較することで自作関数を検証する

自作のdivisors_list_h 関数はsympyモジュールのdivisors関数を比較

自作のdivisors_list_h 関数はsympyモジュールのdivisors関数は同じ機能を持っていることが期待されます。そこで、実際に1から100000まで実行して結果を比較します。結果が異なる場合は”ng”、等しい場合は全部プリントすると膨大になるので1000行毎に”ok”を出力するようにします。

  1. #13 約数を求める関数を検証
  2. for i in range(1,100000):
  3. if divisors_list_h(i)==sympy.divisors(i) :
  4. if i%1000==0:
  5. print(i,divisors_list_h(i),sympy.divisors(i),'ok')
  6. else:
  7. print(i,divisors_list_h(i),sympy.divisors(i),'======>ng')

少なくとも100000までは結果が一致することがわかります。

自作のprime_f関数とsympyモジュールのfactorint関数を比較

  1. #14 素因数分解を辞書形式で求める関数を検証
  2. for i in range(1,100000):
  3. if prime_f(i)==sympy.factorint(i) :
  4. if i%10000==0:
  5. print(i,prime_f(i),sympy.factorint(i),'ok')
  6. else:
  7. print(i,prime_f(i),sympy.factorint(i),'======>ng')

同じように、前作のprime_f関数とsympyモジュールのfactorint関数も結果は同じです。