Pythonによる完全数、友愛数、婚約数の計算

完全数の計算

完全数とは

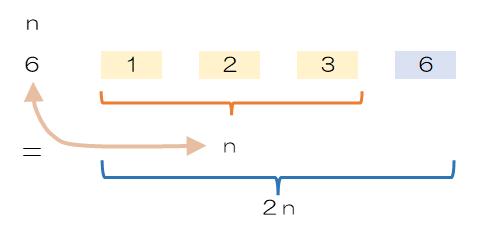
完全数とは、自身が自分自身を除く正の約数の和に等しくなる正の整数のことを指します。1番小さな完全数は6になりますが、n=6について自身6以外の約数は1,2,3となり、その合計は6になります。このため、正の整数nに対して正の約数の合計が2nになるものと考えた方が分かりやすい場合もあります。

完全数
完全数

完全数の計算に特化した、約数の合計を求める関数

整数の約数の個数や合計を計算する関数は、すでに作成しています。

ここでは、完全数の計算に特化した関数を作ります。図のとおり完全数は、自明の約数約数1はカウントしますが、自分自身はカウントされません。そこで、for文で2からnumの平方根までループしnumはカウントされないようにするとともに、1はあらかじめtotalにセットしておきます。

完全数の計算に特化した約数の合計を求める関数
  1. def divisor_perfect(num):
  2. cnt = 1
  3. total = 1
  4. for i in range(2, int(num**0.5)+1):
  5. if num % i == 0:
  6. cnt += 1
  7. total += i
  8. if i**2 == num:
  9. continue
  10. cnt +=1
  11. total+=(int(num/i))
  12. return cnt,total
  14. divisor_perfect(6)

(3, 6)

完全数の計算対象になる約数は1,2,3なので個数3、合計6となります。

完全数の計算

さっそく、完全数を計算します。divisor_perfect関数があれば、すぐに計算できます。とりあえず10000まで計算します。

  1. max=10000
  2. for i in range(2, max+1):
  3. _,total = divisor_perfect(i)
  4. if total == i:
  5. print (i,end=',')

6,28,496,8128,

1も完全数の要件にあてはまりそうな気もしますが、通常は6が一番小さな値になります。10000までの間に4つの完全数がみつかります。これより大きなものは、次の通りです。

33550336,

8589869056,

137438691328,

2305843008139952128,

2658455991569831744654692615953842176,

191561942608236107294793378084303638130997321548169216,

13164036458569648337239753460458722910223472318386943117783728128,

14474011154664524427946373126085988481573677491474835889066354349131199152128

急速に巨大な数値になります。計算が大変なので、完全数を次のようにリストに収めます。

  1. perfect=[6,
  2. 28,
  3. 496,
  4. 8128,
  5. 33550336,
  6. 8589869056,
  7. 137438691328]

友愛数を求める

異なる2つの正の整数の組で、自身を除いた約数の和が、互いに他方と等しくなるような数を友愛数（amicable numbers）といいます。

例えば220の自身を除いた約数は、1,2,4,5,10,11,20,22,44,55,110で、これらの和は 284とりなります。この284の自身を除いた約数は、1, 2, 4, 71, 142 で、その合計は220と元の整数に戻ります。さっそく、友愛数を計算します。

友愛数を計算するプログラム

友愛数の計算
  1. amical_l = []
  2. for i in range(1, 100000 + 1):
  3. amical = divisor_perfect(i)
  4. if amical <= i:
  5. continue
  6. if divisor_perfect(amical) == i:
  7. amical_l.append([i,amical])
  9. amical_l

[[220, 284],
 [1184, 1210],
 [2620, 2924],
 [5020, 5564],
 [6232, 6368],
 [10744, 10856],
 [12285, 14595],
 [17296, 18416],
 [63020, 76084],
 [66928, 66992],
 [67095, 71145],
 [69615, 87633],
 [79750, 88730]]

友愛数を単純に並べる

友愛数は、名前からしてペアになるのでリストの中にさらにペアを入れ込むようにしましたが、これを単純な数字の並びにします。

友愛数を単純に並べる
  1. sum(amical_l,[])

[220,
 284,
 1184,
 1210,
 2620,
 2924,
 5020,
 5564,
 6232,
（以下略）

婚約数の計算

異なる2つの正の整数の組で、1と自分自身を除いた約数の和が、互いに他方と等しくなるような整数を婚約数（betrothed numbers）といいます。早速、婚約数を求めるプログラムを作成します。約数の合計の際に1を含めないだけですが、随分と結果が異なります。

婚約数の計算
  1. betrothed_l = []
  2. for i in range(1, 100000 + 1):
  3. betrothed = divisor_perfect(i)-1
  4. if betrothed <= i:
  5. continue
  6. if divisor_perfect(betrothed)-1 == i:
  7. betrothed_l.append([i,betrothed])
  9. betrothed_l

[[48, 75],
 [140, 195],
 [1050, 1925],
 [1575, 1648],
 [2024, 2295],
 [5775, 6128],
 [8892, 16587],
 [9504, 20735],
 [62744, 75495]]