Pythonで順列、組合せの計算をする

Pythonで順列、組合せの計算をします。

定義通りの方法で順列、組合せの計算をする

順列の計算

Pythonでは順列は次の方法で計算します。Pはpermutationの略です。

$\displaystyle {}_n\ P_r = n(n-1)(n-2)・・・(n-r+1)=\frac{n!}{(n-r)!}$

$_5\ P_3=5×4×3=60$の計算をします。

#1 定義通りの方法で順列の計算をする
def nPr(n,r):
npr=1
for i in range(n,n-r,-1):
npr*=i
return npr
nPr(5,3)

定義の通り、3行目で順列を計算する変数nprを定義します。5行目で掛け算をしていくので初期値は1になります。

n=5、r=3とするとn-r=2となりますが、4行目のrange関数では(5,2,-1)とすると3つめの引数が-1なので5から1ずつ遡り、2の手前の3までの累積を計算します。

組合せの計算

組合せの計算は次のとおりです。Cはcombinationの略です。

$\displaystyle {}_n C_r = \frac{n(n-1)(n-2)\cdots (n-r+1)}{r\times (r-1)\times \cdots 2 \times 1}=\frac{_n P _r}{r!}=\frac{n!}{r!(n-r)!}$

前節の順列をr!で割ればよいので、順列を計算する関数を使います。ここでは$_5\ C_3=(5×4×3)/( 5×4×3)$の計算をします。

#2 定義通りの方法で組合せの計算をする
def nCr(n,r):
factr =1
r = min(r, n-r)
for i in range(r,1,-1):
factr*=i
return nPr(n,r)/factr
nCr(5,3)

nCr関数の中でnPr関数が使われているので、#1があらかじめ実行されていることが前提となります。定義通りの方法で簡単に計算することができますが、nやrが大きくなると階乗を求めるためには計算量が膨大になるため工夫が必要になります。

組合せの公式を使った再帰計算

nとrが1ずつ増える場合の定理

組合せには次の有名な定理があります。

$r\hspace{5px} _n C_r =n\hspace{5px} _{n-1}C_{r-1}\hspace{15px}==>\displaystyle_n C_r =\frac{n}{r}\displaystyle _{n-1}C_{r-1}$

数学的な証明はさておき、n人からr人のメンバーを選び、さらにそのr人のメンバーから1人のｐリーダーを決めることを考えます。組合せは、$r×_nC_r$になります。いっぽう、先にn人の中から1人リーダーを決めて、残ったn-1人からリーダー以外のr-1人のメンバーを選ぶと考えます。組合せは、$n×_{n−1}C_{r−1}$になります。これらの2つの式は同じことを言っているので等しくなります。

#3 組合せの定理から再帰関数により組合せを計算する
def comb_r(n, r):
if r==0:
return 1
return comb_r(n-1, r-1) * n / r
comb_r(5,3)

10.0

１　関数が呼び出されると、5行目でcomb_r(n-1, r-1)、つまりn=4,r=2として２が実行されます。１の制御はしばらく保留されます。

２　5行目でcomb_r(n-1, r-1)、つまりn=3,r=1として３が実行されます。

３　5行目でcomb_r(n-1, r-1)、つまりn=3,r=1として４が実行されます。

４　3行目でr=0なので、３に戻り値1を返します。３では、４からの戻り値にn/r倍して２に戻り値3を返します。２では３からの戻り値6を5/3倍します。

上記の結果、最初に呼び出されたものも含め、関数が5回実行されています。それぞれ、returnの返り値はそれぞれのn,rの組合せの値を1つ前の関数に戻しています。

分割の定理

もう一つ、組合せの分割について有名な定理があります。

$\ _n C_r=\ _{n-1}C_r+_{n-1}C_{r-1}\hspace{15px}(n\geqq r)$

n人からr人を選ぶときに、ある特定の1人に注目します。その人が選ばれない場合、n-1人からr人を選べ組合せを考えればよく、その人が選ばれる場合はn-1人からr-1人を選ぶ組み合わせを考えればよいわけです。両者は独立して起こるので、両者を合計すればよいわけです。ここでは計算を簡単にするため$_4C_2$の計算をします。

#4 組合せの分割の定理から再帰関数により組合せを計算する
def comb(n,r):
if r == 0:
return 1
elif n < r:
return 0
else:
return comb(n-1, r) + comb(n-1, r-1)
comb(4,2)

このプログラムは定理をそのまま表していますが、これでなぜ正しく計算できるのかを見るために、関数に入った時に引数nとrを表示するためprint文を入れます。また、実行順番を示すためiをカウンタとして同時に表示します。

#5 再帰関数の流れを理解する
def C(n,r):
global i
i+=1
print('#'+str(i),'呼び出し n=',n,'r=',r)
if r == 0:
return 1
elif n < r:
return 0
else:
return C(n-1, r) + C(n-1, r-1)
i=0
C(4,2)

#1 呼び出し n= 4 r= 2
#2 呼び出し n= 3 r= 2
#3 呼び出し n= 2 r= 2
#4 呼び出し n= 1 r= 2
#5 呼び出し n= 1 r= 1
#6 呼び出し n= 0 r= 1
#7 呼び出し n= 0 r= 0
#8 呼び出し n= 2 r= 1
#9 呼び出し n= 1 r= 1
#10 呼び出し n= 0 r= 1
#11 呼び出し n= 0 r= 0
#12 呼び出し n= 1 r= 0
#13 呼び出し n= 3 r= 1
#14 呼び出し n= 2 r= 1
#15 呼び出し n= 1 r= 1
#16 呼び出し n= 0 r= 1
#17 呼び出し n= 0 r= 0
#18 呼び出し n= 1 r= 0
#19 呼び出し n= 2 r= 0

１　関数が呼び出されると、11行目のelse節に入り、2つある関数のうち左側のC(n-1, r) ２がn=3、r=2として呼び出され、制御が移動します。右側の13はC(n-1, r-1)は２が終了し返り値を戻した後に実行されるのでかなり先のことになります。

２　１と同様に11行目の左側のC(n-1, r)３がn=2、r=2として実行されます。

３　同様に11行目の左側のC(n-1, r)４がn=1、r=2として実行されます。

４　8行目でnはrより小さいので、戻り値0を３に返します。３では、11行目の右側のC(n-1, r-1)５が呼び出されます。

５　11行目のelse節に入り、2つある関数のうち左側のC(n-1, r)６がn=0、r=1として実行されます。

６　6行目に入り0を５に戻します。５では右側の C(n-1, r-1)７が実行されます。

７　7が戻り値1を５に返すと、5の11行目の2つの関数の結果が出そろうので、合計=1を３に返します。同様に３は２に1を返します。２では11行目の左側の関数が戻り値1を返すので、右側の８C(n-1, r-1)が実行されます。

８　以降同じように動いていきます。ここで９から12の流れが、14からも15から18として繰り返し実行されます。

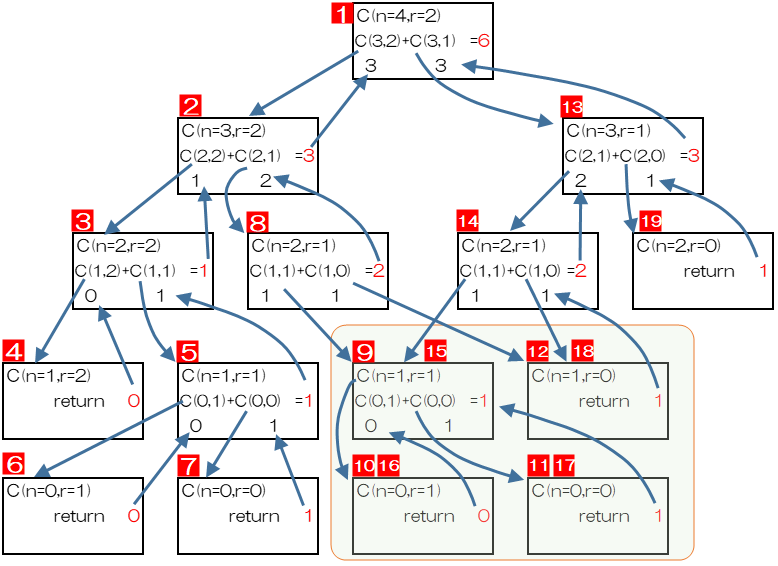
このように、単純な組合せもこの再帰関数でが17回、実行されます。

SciPyモジュールによる順列、組合せの計算

NumPyモジュールやSymPyモジュールには順列や組合せを計算する関数が用意されていません。統計関係の関数はSciPyモジュールに見付けることができます。

#6 scipyモジュールを使った順列、組合せの計算
import scipy.special
print(scipy.special.perm (5,3))
print(scipy.special.comb (5,3))

60.0
10.0

SciPyモジュールにはNumPyのndarray配列を使うと複数の順列、組合せの計算をまとめてすることができます。

#7 SciPyモジュールとNumPyモジュールを使った順列組合せの配列計算
import numpy as np
import scipy.special
np.set_printoptions(precision=2, suppress=True)
n_array = np.array([5, 10, 15, 20])
r_array = np.array([3, 5, 7, 9])
print(scipy.special.perm(n_array, r_array))
print(scipy.special.comb(n_array, r_array))
print(scipy.special.comb(n_array, 3))

[6.00e+01 3.02e+04 3.24e+07 6.09e+10]
[    10.    252.   6435. 167960.]
[  10.  120.  455. 1140.]

5行目、6行目でNumPyのndarray配列を定義し、7行目でSciPiモジュールのperm関数で順列を、8行目ではcomb関数で組合せを、それぞれ配列計算しています。また、9行目ではnを4つの数字を収めた配列、rを数字（スカラー）で指定することもできます。

不思議なことに、配列にすると表示は指数表示になってしまいます。そこで、4行目のset_printoptionsを実行しています。このことにより組合せは整数表示になりますが、順列は指数表示のままです。