Pythonによる三角比の計算

Pythonには三角関数についても強力な機能があります。ここでは、簡単な事例を紹介します。

Pythonにおける三角関数の考え方

degreeとradianの関係

Pythonで関数に角度を引数として渡す場合、30°というようなdegreeよりも、$\pi/6$のようなradianが使われます。30°というのは直感的につかむことができてもradianといわれるとピンとこないのでこの関係を確認します。$\pi$は円周率をあらわし、180°が$\pi(≒3.14)$radianになります。

$\displaystyle \large{ { 1 \mathrm{ [rad] } = \frac{180}{\pi} ^\circ } }$

$\large{ { 180^\circ = \pi \mathrm{ [rad] } } }$

この関係をmathモジュールで$\pi$に関する計算をすることにより確認します。

#1 radianとdegreeの関係
import math
print('pi=','{:.5f}'.format(math.pi))
rad=180/math.pi
print('1[rad] =','{:.3f}'.format(rad),'°')
deg=math.pi/180
print('1degree =','{:.5f}'.format(deg),'[rad]')

pi= 3.14159
1[rad] = 57.296 °
1degree = 0.01745 [rad]

$\pi$は約3.14、1radian=57.296$\circ$、1$^\circ$=0.017radianということになります。

degreeとradianの換算

degreeとradian相互間を変換する関数を確認します。

mathモジュール

mathモジュールでは、radians関数でdegreeからradianに、degrees関数でradianからdegreeに変換することができます。

#2 mathモジュールによるradianとdegreeの変換
print(math.radians(30))
print(math.degrees(math.pi/6))

0.5235987755982988
29.999999999999996

端数の関係で誤差が出ますが、$30^\circ$は$\pi/6$radianなので、うまく計算できていることがわかります。

NumPyモジュール

NumPyモジュールでは、rad2deg関数でradianからdegreeへ、dsg2rad関数で、degreeからradianに変換することができます。NumPyなので配列をまとめて扱うことができます。

ここでは、radpiに様々なradianの値を$\pi$を使ってndarrayの配列として、degreeに変換したのち、radianに戻しています。

#3 NumPyモジュールによるradianとdegreeの変換
import numpy as np
radpi = np.array([np.pi/6,np.pi/4, np.pi/3,np.pi/2, np.pi,3*np.pi/2,2*np.pi])
deg=np.rad2deg(radpi)
print(np.round(deg,0))
rad=np.deg2rad(deg)
print(np.round(rad,3))

[ 30.  45.  60.  90. 180. 270. 360.]
[0.524 0.785 1.047 1.571 3.142 4.712 6.283]

まとめると、次の表のようになります。

Radian	Degree	Radian
π/6	30°	0.524
π/4	45°	0.785
π/3	60°	1.047
π/2	90°	1.571
π	180°	3.142
3π/2	270°	4.712
2π	360°	6.283

SymPyモジュール

SymPyモジュールではdeg関数でradianからdegreeへ、rad関数で、degreeからradianに変換することができます。

#4 SymPyモジュールによるradianとdegreeの変換
import sympy
rad30=sympy.rad(30)
deg30=sympy.deg(rad30)
display(deg30,rad30)

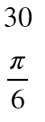
MathモジュールやNumPyモジュールではradianに変換すると少数表示になりますが、SymPyモジュールでは平方根を使った表示になります。

三角比を計算する関数

Pythonで三角比を計算する関数をご紹介します。ここでは、$\pi/6=30^\circ$を例に計算します。

$\sin(30^\circ)=\sin(\pi/6)=\frac{1}{2}=0.5$

$\cos(30^\circ)=\cos(\pi/6)=\frac{\sqrt{3}}{2}\fallingdotseq0.866$

$\tan(30^\circ)=\tan(\pi/6)=\frac{\sqrt{3}}{3}\fallingdotseq0.577$

math関数による三角比の計算

mathモジュールではsin,cos,tan関数を使い三角比を計算します。このときの角度はradianで指定することになります。

radianから三角比を計算する

#6 Mathモジュールでの変換定数
import math
rad=math.pi/6
print(math.sin(rad))
print(math.cos(rad))
print(math.tan(rad))

0.49999999999999994
0.8660254037844387
0.5773502691896257

結果は小数で表示されます。

degreeからradianに変換して三角比を計算する

三角関数に$ 30^\circ$のようなdegreeで引数を渡すときには、radians関数でradianに変換します。

#7 Mathモジュールでdegreeから変換定数
import math
deg=30
print(math.sin(math.radians(deg)))
print(math.cos(math.radians(deg)))
print(math.tan(math.radians(deg)))

0.49999999999999994
0.8660254037844387
0.5773502691896257

結果は、#6と同じです。

NumPy関数による三角比の計算

#6で$\sin( 30^\circ)=\sin(\pi/6)$は0.5であることがわかりました。逆に0.5はsinで何度かを知るためにはarcsin関数を使います。

#8 Mathモジュールでarcsinを計算する
print(math.asin(0.5))
print(math.pi/6)
print(math.degrees(math.asin(0.5)))

0.5235987755982989
0.5235987755982988
30.000000000000004

SymPy関数による三角比の計算

SymPyモジュールでも三角比の計算が可能です。

#10 SymPyモジュールによる三角比の計算
import sympy
rad=sympy.pi/6
display(sympy.sin(rad))
display(sympy.cos(rad))
display(sympy.tan(rad))

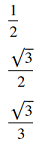
SymPyモジュールの特徴は、ちょうどよい角度のときには平方根を使って表示されることです。