Pythonによる自然対数、logの計算

Pythonには自然対数や対数logについても強力な機能があります。

Pythonにおける三角関数の考え方

自然対数を表示する

mathモジュールによる自然対数の計算

Pythonで自然対数をmathモジュールで計算します。

#1 mathモジュールによる自然対数の計算
import math
print(math.e)
print(math.e**3)
print(math.exp(3))

2.718281828459045
20.085536923187664
20.085536923187668

自然対数は、「鮒一鉢二鉢一鉢二鉢至極惜しい」（”い”は５）と語呂合わせで覚えますが、結果は正しいようです。また、4行目でeを3乗し、5行目でexp関数を使い計算します。最後の桁で誤差が出ています。

decimalモジュールによる自然対数の計算

小数点以下を正確に計算するためにはdeimalモジュールを使います。

#2 decimalモジュールによる自然対数を
import decimal
decimal.getcontext().prec = 30
print(decimal.Decimal(1).exp())
print(decimal.Decimal(3).exp())

2.71828182845904523536028747135
20.0855369231876677409285296546

decimalモジュールでは、getcontext().precで有効桁数を指定することができます。ここでは3行目で30桁まで計算しています。#1のe^3とexp(3)の誤差についてみるとexp関数の方が正しいようです。

自然対数の定義に基づく計算

自然対数の定義は次の通りです。

自然定数の定義

$e=\displaystyle\lim_{h\to\infty}\left(1+\frac{1}{h}\right)^{h}$

定義に従って計算するとhを無限に大きくする必要があります。hを順次増やしていくと次のようになります。hを10000まで計算し、1000毎にprint文で表示しています。

#3 定義に従って自然対数を計算
for h in range(1,10001):
e=(1+1/h)**h
if h%1000==0:
print('h=',h,':',e)

h= 1000 : 2.7169239322355936
h= 2000 : 2.7176025693228403
h= 3000 : 2.7178289198743233
h= 4000 : 2.717942121080266
h= 5000 : 2.718010050101555
h= 6000 : 2.718055339575291
h= 7000 : 2.718087690895448
h= 8000 : 2.7181119553078
h= 9000 : 2.7181308281830128
h= 10000 : 2.7181459268249255

#2と比較するとhを10000まで計算して2.718、つまり小数点以下第3位までは正しく計算できることになります。

NumPy,SymPyモジュールによる自然対数

NumPyモジュールによる自然対数の計算

NumPyモジュールでも自然対数を計算することができます。NumPyモジュールの特徴は配列をまとめて計算できることです。

#4 NumPyモジュールで自然対数の10乗まで計算する
import numpy as np
np.set_printoptions(precision=3,suppress=True)
array = np.arange(1,11)
expon=np.exp(array)
expon

array([    2.718,     7.389,    20.086,    54.598,   148.413,   403.429,
        1096.633,  2980.958,  8103.084, 22026.466])

NumPyモジュールでは数値表現は指数表示になり、慣れない見づらいところがあります。単純に計算すると、2.98095799e+03のような表現になります。e+03というのは10の3乗という意味で、2980.95799を表します。このためprintoptions関数で、小数点以下を3桁に表示するように変更します。

PythonのNumPyモジュールの数値の表示を見やすくする

SymPyモジュールによる自然対数の計算

#5 SymPyモジュールで自然対数の計算をする
import sympy
expon=sympy.E
expon3=sympy.exp(3)
display(Math('e='+str(expon.evalf(30))))
display(Math('e^3='+str(expon3.evalf(30))))

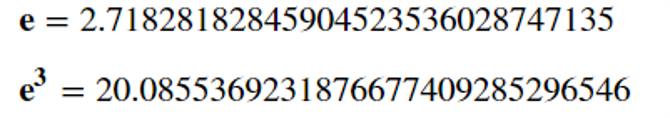
SymPyモジュールでは、自然対数は大文字のEを使って表します。べき乗するときはexp関数を使います。それぞれ、数値の内容を表示するためにはevalfメソッドを使います。evalifの()の中に何も指定をしないと有効桁数15桁程度になりますが、桁数を指定することができます。桁数は1万桁でも指定できますが正確かどうかは検証していません。

対数の計算をする

mathモジュールで対数の計算をする

mathモジュールを使って対数（log）の計算をします。対数の計算は底が2,10,自然対数の場合が多いので、それぞれ関数が用意されています。また、これ以外の数字を底とするための関数もあります。

$2^3=8 \hspace{8pt} \log_2 8=3$

$10^3=1000 \hspace{8pt} \log_{10} 1000=3$

$e^3 \fallingdotseq 20.085536923187668 \hspace{8pt} \log_{e} 20.085536923187668 \fallingdotseq 3$

#6 mathモジュールで対数の計算をする
import math
log_2=math.log2(8)
log_d=math.log10(1000)
log_3=math.log(27,3)
log_e=math.log(20.085536923187668)
print(log_2,log_d,log_e,log_3)

3.0 3.0 3.0 3.0

3行目のようにmathモジュールでは、底が2のときは、log2関数を使います。
4行目のように底が10のときには、log10関数を使います。
5行目のように底が2,10のときは、log関数を使い、2つ目の引数に底を渡します。ここでは、底が3としています。
6行目のようにlog関数に2つ目の引数（底）を省略すると、自然対数eを底として計算します。

NumPyモジュールによる対数の計算

Numpyモジュールでもmathモジュールと同様に対数の計算をすることができます。

#7 NumPyモジュールで対数の計算をする
import numpy as np
log_2 = np.log2(8)
log_d = np.log10(1000)
log_e = np.log(20.085536923187668)
log_3=np.log(27)/np.log(3)
log_1p = np.log1p(19.085536923187668)
print(log_2,log_d,log_e,log_3,log_1p)

3.0 3.0 3.0 3.0 3.0

2,3行目のように、2,10を底にするときは、log2、log10関数を使います。
4行目のように自然対数を底とするときはlog関数を使うことができますが、これ以外の底で計算する関数が見当たりません。
5行目のように、次の式に従い、自然対数などを底として割り算をして求めるほかないようです。$\displaystyle \log_a x = \frac{log_bx}{log_ba}$
その代わり、log_1p関数で、底を自然対数としてlog(1+x)を計算することができます。6行目のように、20.855・・から1を引いた19.855・・を渡すと、4行目と同じ結果を返します。テイラー展開を想定しているものと思われます。

SymPyモジュールによる対数の計算

#8 SymPyモジュールで対数の計算をする
import sympy
log_2 = sympy.log(8,2)
log_d = sympy.log(1000,10)
log_e = sympy.log(20.085536923187668)
log_e = sympy.log(20.085536923187668,sympy.E)
log_3=sympy.log(27,3)
print(log_2,log_d,log_e,log_3)

3 3 3.00000000000000 3

SymPyモジュールの基本的な関数には、log2関数などは用意されていません。その代わり、log関数の2つ目の引数で底を指定することができます。5行目のように、2つ目の引数である底を省略すると自然対数を底として計算されます。6行目にように積極的に自然対数を指定することもできます。