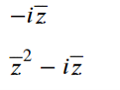Numpy Sympyで複素数の計算をする
Pythonで複素数について計算するときに、NumPyモジュールやSymPyモジュールを使うと、より応用的な計算をすることができます。
NumPy、SymPyモジュールによる複素数の基本的な計算
虚数単位の計算
NumPyモジュールでは、ndarrayとして配列を定義すると、複数の複素数について同時に演算をすることができます。
NumPyモジュールによる複素数の計算
- #1 NumPyモジュールによる複素数の四則演算
- import numpy as np
- a = np.array([1+1j, 1+2j, 1+3j])
- b = np.array([1+1j, 2+1j, 3+1j])
- print(a+b)
- print(a-b)
- print(a*b)
- print(a/b)
- print(type(a+b))
- print(np.real(a))
- print(np.imag(a))
- print(np.conj(a))
[2.+2.j 3.+3.j 4.+4.j] [ 0.+0.j -1.+1.j -2.+2.j] [0. +2.j 0. +5.j 0.+10.j] [1. +0.j 0.8+0.6j 0.6+0.8j][1. 1. 1.] [1. 2. 3.] [1.-1.j 1.-2.j 1.-3.j]
- 3、4行目で複素数を含んだndarray形式の配列を定義します。
- 5~8行目で四則演算をしています。結果は9行目でわかるようにndarray形式で返されます。
- 9行目以下のとおり、実部はreal関数、虚部はimag関数、共役複素数はconj関数で計算することができます。
SymPyモジュールによる虚数の定義と計算
SymPyモジュールでは、虚数単位を大文字のIで表します。
- #2 SymPyモジュールによる虚数の定義
- import sympy
- print(sympy.I)
- print((sympy.I)**2)
I -1
SymPyでは虚数単位は英大文字のIで表します。Iを2乗すると定義通り-1になります。
SymPyモジュールの複素数に関する関数
SymPyモジュールにも複素数に関する基本的な関数が用意されています。
- #3 SymPyモジュールによる複素数に関する基本的な関数
- import sympy
- c = 2+3*sympy.I
- print(sympy.re(c))
- print(sympy.im(c))
- print(c.as_real_imag())
- print(sympy.conjugate(c))
2 3 (2, 3) 2 - 3*I
- SymPyモジュールでは3行目のようにIを使って複素数を定義します。
- 4行目のようにas_real_imagメソッドにより、実部と虚部をタプルにすることができます。
- 5行目以下のとおり実部はre関数、虚部はim関数、共役複素数はconjugate関数で計算することができます。
SymPyモジュールによる代数計算
SymPyモジュールによる代数計算の基礎
SymPyによる複素数の代数としての定義
SymPyモジュールには、複素数の代数計算をする機能が用意されています。
- #4 SymPyモジュールによる代数計算
- import sympy
- sympy.var('z', complex=True)
- display(z)
- display(sympy.expand_complex(z))
- display(sympy.conjugate(z))
- display(sympy.expand_complex(sympy.conjugate(z)))
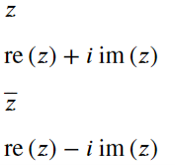
- 2行目にようにSymPyで変数を定義するとき”complex=True”と指定すると、複素数として取り扱うことができます。
- 3行目のように単純に出力するとzとしか表示されませんが、4行目のようにexpand_complex関数を使うと実部と虚部を分けて表示することができます。
- 5行目のようにconjugate関数を使うと$\overline{Z} $のように共役複素数の表現をすることができます。これに対して6行目のようにexpand_complex関数を使うと、共役複素数を実部と虚部を分けて表示させることができます。
SymPyモジュールで代数に複素数の値を代入した場合の計算
SymPyモジュールで、変数に具体的な複素数を代入したのち、前節と同じ計算をすると次のとおりになります。
- #5 SymPyモジュールで代数に複素数の値を代入した場合の計算
- import sympy
- z=1+2*I
- display(z)
- display(expand_complex(z))
- display(conjugate(z))
- display(expand_complex(conjugate(z)))
1+2𝑖 1+2𝑖 1−2𝑖 1−2𝑖 1+2𝑖
変数zに値が代入されているので、expand_complex関数を使っても単純な複素数の表示になります。
SymPyにより複素数の基本的な定理を計算する
SymPyによる共役複素数の計算
共役複素数について基本的な公式は次の通りです。
$\overline{\alpha+\beta}=\overline{\alpha}+{\overline{\beta}}$
$\overline{\alpha\beta}=\overline{\alpha}{\overline{\beta}}$
$\displaystyle \overline{ \left( \frac{\alpha}{\beta} \right) } = \frac{ \overline{ \alpha } }{ \overline{ \beta } }\quad(\beta \neq 0)$
$\overline{\overline{\alpha}}=\alpha$
$\displaystyle \frac{\alpha+\overline{\alpha}}{2}=re(\alpha)$
$\displaystyle \frac{\alpha-\overline{\alpha}}{2}=img(\alpha)$
SymPyの代数計算を使えば、これらの公式をかくにんすることができます。
- #6 SymPyで計算する複素数の基本的な定理
- var('alpha beta',complex=True)
- display(conjugate(alpha+beta))
- display(conjugate(alpha*beta))
- display(conjugate(alpha/beta))
- display(sympy.conjugate(sympy.conjugate(alpha)))
- display(expand_complex((alpha+conjugate(alpha))/2))
- display(expand_complex((alpha-conjugate(alpha))/(2*I)))
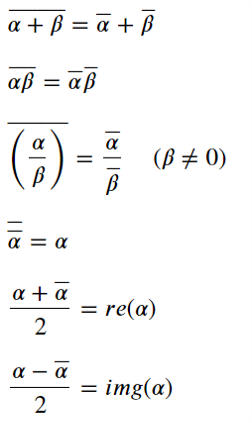
SymPyによる代数計算の応用
次の定理は受験参考書を見ると自明なものとしてでてきますが、しっかり意識しておかないと計算ミスにつながります。このような定理もSymPyの代数計算を使えば確認することができます。
- #7 複素数の基本定理2
- sympy.var('z',complex=True)
- display(sympy.conjugate(sympy.I*z))
- display(sympy.conjugate(z**2+sympy.I*z))