極座標グラフの作成と複素数平面での極形式の計算

複素数を扱うことができる大きなメリットとして、複素数平面によるさまざまな演算ができることが挙げられます。複素数平面について理解するうえで極座標グラフを書くと理解しやすくなります。そこで、matplotlibにより極座標グラフを作成し、複素数平面の考え方を整理したうえで、NumPyモジュール、cmathモジュールやSymPyモジュールを使い、基本的な複素数平面の計算をします。

複素数平面と極座標グラフ

複素数平面の考え方

複素数は次の形式で表現します。

複素数の表現
複素数の表現

極座標グラフを作成する

極形式の考え方

簡単な例として、$z=1+\sqrt{3}i$という複素数を考えると、定義から$a=1,b=\sqrt{3}$になります。ここで、極座標グラフを書くと、x軸に実部$1$を、y軸に虚部$\sqrt{3}$を取ってグラフにすると、下図のようになります。

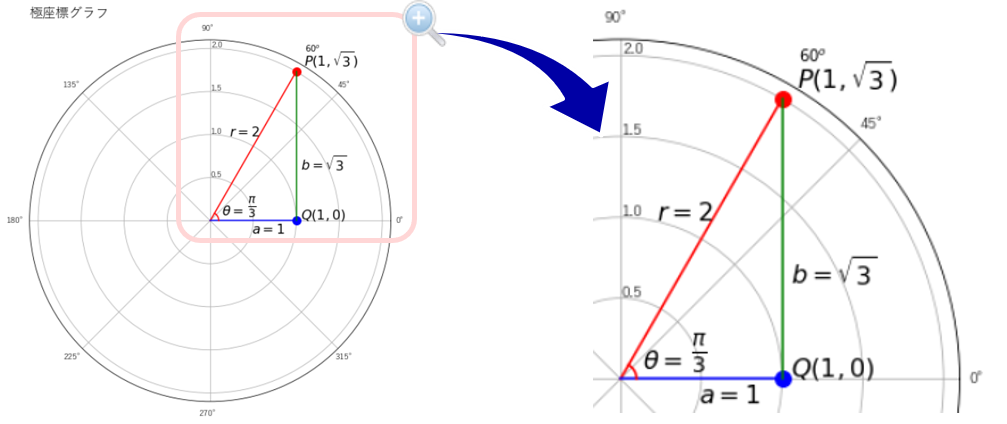
複素数平面のグラフ
複素数平面のグラフ

$a=1,b=\sqrt{3}$を表した点$ P(1,\sqrt{3})$は、原点からの距離r（絶対値）と、半直線OPがx軸の正の向きとなす角度を$\theta$で表すことができます。$\theta$は偏角(argument)といい、$arg z$と表現します。絶対値、偏角は次の通り計算します。

絶対値：$r=|z|=\sqrt{a^2+b^2}=\sqrt{1^2+\sqrt{3}^2}=2$

偏　角：$\displaystyle tan\theta=\frac{b}{a}=\sqrt{3}\qquad \therefore \theta= arctan\sqrt{3}=\frac{\pi}{3} (60^o)$

逆に、絶対値と偏角からzの実部、虚部は、次の通り計算することができます。

実　部:$\displaystyle x= r\cos\theta=2×\cos\frac{\pi}{3}=1$

虚　部:$\displaystyle y= r\sin\theta=2×\sin\frac{\pi}{3}=\sqrt{3}$

そこで、極形式という方法で複素数$1+\sqrt{3}i$を表すと次のようになります。

極形式：$ \displaystyle z=r(\cos\theta+i\sin\theta)=2(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3} )\quad r\gt0 \quad \theta=arg z$

最終的には極形式として$1+\sqrt{3}i$をあらわすと、$\displaystyle r=2$と$\theta=\frac{\pi}{3}$と表現することができます。

matplotlibのpolar projectionによる極座標グラフの作成

matplotlibでpolarというprojectionを使うと描くことができます。極座標グラフの最大の特徴は、座標を$(x,y)$ではなく、絶対値、rと角度thetaの組合せで表すことです。

  1. #1 極座標グラフ（複素数平面のグラフ）を作成する
  2. import numpy as np
  3. import matplotlib.pyplot as plt
  4. from matplotlib import rcParams
  5. %matplotlib inline
  6. # 日本語が文字化けしないようにフォントを設定
  7. rcParams['font.family'] = 'sans-serif'
  8. rcParams['font.sans-serif'] = ['Hiragino Maru Gothic Pro', 'Yu Gothic', 'Meirio', 'Takao', 'IPAexGothic', 'IPAPGothic', 'Noto Sans CJK JP']
  9. #グラフの定義
  10. fig = plt.figure(figsize=(8, 8))
  11. ax = plt.subplot(projection='polar')
  12. #絶対値と偏角の定義
  13. r = 2
  14. theta = np.pi/3
  15. #グラフを描くための変数の定義
  16. n=1000
  17. x_range = np.linspace(0, r * np.cos(theta), n)
  18. theta_range = np.linspace(0, theta, n)
  19. #グラフの部品を個別の描画
  20. ax.set_title('極座標グラフ',fontsize=16) #見出し
  21. ax.plot(theta,r-0.03,marker='o',color='r',markersize=10) #点Pの●
  22. ax.plot((0, theta), (0, r),color='r') #原点から点Pまでの半直線
  23. ax.plot( np.zeros(n), x_range, color='b') #原点から(1,0)までの半直線
  24. ax.plot(theta_range, r * np.cos(theta) / np.cos(theta_range), color='g') #(1,0)から点Pまでの半直線
  25. ax.plot(theta_range, np.ones(n) * 0.1, color='r') #角度のマーク
  26. ax.set_rmax(2) #半径の最大値
  27. ax.set_rticks((0.5, 1, 1.5, 2)) # 軸の目盛
  28. ax.set_rlabel_position(271.5) #軸目盛のラベルの表示位置
  29. ax.text(theta-0.07, r+0.1 , r'$P(1,\sqrt{3})$',fontsize=16) #点Pの座標の表示
  30. ax.text(theta+0.01, r+0.04 , r'$ 60^o$') #60度の角度の表示
  31. ax.text(theta+0.2, 1 , r'$r = 2$') #r=2の表示
  32. ax.text(0-0.2, 0.5, r'$a = 1$') #a=1の表示
  33. ax.text(0.5, 1.2, r'$b = \sqrt{3}$') #b=root3の表示
  34. ax.text(0.45, 0.15, r'$\theta = $') #角度の"theta="の表示
  35. ax.text(0.25, 0.35, r'$\frac{\pi}{3}$',fontsize=16) #n/piの表示
  36. plt.show()

  1. 11行目でグラフを定義するとき、’projection=polar’とすると、極座標グラフを作成することができます。
  2. 13行目で絶対値をr、14行目で偏角をthetaとして定義します。
  3. 極座標グラフでは、座標を表すときには偏角、絶対値の順に定義します。例えば21行目で点$ P(1,\sqrt{3})$を赤点で表示していますが、theta=$\frac{\pi}{3}$、r=2（グラフの見栄えから0.03ほど内側にしています）として定義しています。
  4. 23行目では、原点から点Pまでの赤い直線を描いています。(0, theta), (0, r)とあるのは、偏角=0、絶対値=0つまり原点から、点P (r,theta)=(2, $\frac{\pi}{3}$)まで直線を引くように指示しています。
  5. 24行目では、原点から点Q(1,0)までの青い半直線を描いています。偏角をn(=1000)個に細かく区分し、np.zeros(n)で0がn個入った配列を定義し、r_rangeを0から1までの間で1000個に区分した配列と対応させています。つまり、角度0で、絶対値rを軸に沿って0から1まで増やすことにより描画していることになります。
  6. 25行目で、Q(1,0)から点$ P(1,\sqrt{3})$までの緑色の半直線を描いています。偏角を0からthetaまでn個に区分し少しずつ増やしますのに合わせ、絶対値を1から$\sqrt{3}$まで少しずつ増やすようにしています。絶対値については、この場合r * np.cos(theta)で１を計算し、これを np.cos(theta_range)で割ることにより、theta_rangeが0からthetaまで増えるに従い、$\sqrt{3}$まで増やすようにすることができます。とても単純な直線ですが、極座標だと思いのほか複雑になります。
  7. このほか、極座標グラフの特徴で面白い点として、28行目では軸目盛をグラフの半径で、29行目では軸目盛のラベルの表示位置も角度で指定しています。

絶対値と偏角の計算

組み込み関数とmathモジュールの関数による極形式の計算

複素数関数の定義に従い、pythonの基本的組み込み関数とmathモジュールの関数を使い、絶対値、偏角の計算をします。

  1. import math
  2. z=complex(1,math.sqrt(3))
  3. print((z.real**2+z.imag**2)**0.5)
  4. print(abs(z))
  5. print(math.atan(z.imag/z.real)/math.pi)
  6. print(math.degrees(math.atan(z.imag/z.real)))

2.0
1.9999999999999998
0.3333333333333333
59.99999999999999

  1. 2行目で、変数zをcomplex関数により使い定義します。
  2. 3行目では、real属性とimag属性を取り出し、それぞれ2乗した数値の和に対し、平方根を取った値が絶対値になります。
  3. 偏角はarctanで計算されます。このときの計算結果は小数点つきのradianで計算されるので、とよくわからない数字になってしまいます。
  4. 3の値を$\pi$で割ると0.3333・・、つまり1/3でああり、$\pi/3$であることがわかります。
  5. これをmathモジュールのdegrees関数で弧度法に変換すると60度となり、図の結果と一致します。
  6. このことからr=2,$\theta=60$となります。

NumPyモジュールによる極形式の計算

NumPyモジュールを使うと、複素数の極形式（絶対値、偏角）を配列でまとめて計算することができます。

  1. import numpy as np
  2. zn = np.array([1+np.sqrt(3)*1j,np.sqrt(3)+1j,1+1j])
  3. print(np.abs(zn))
  4. print(np.angle(zn))
  5. print(np.degrees(np.angle(zn)))

[2.         2.         1.41421356]
[1.04719755 0.52359878 0.78539816]
[60. 30. 45.]

  1. 2行目のようにNumPyモジュールでは、複素数をndarray形式で配列として定義し、一括して計算することができます。
  2. 3行目のように、abs関数で絶対値を計算することができます。
  3. 4行目のようにangle関数で、偏角を計算することができます。結果は、radianで表示されます。
  4. 5行目にようにradianを弧度法に変換するためには、degrees関数を使います。

cmathモジュールによる極形式の計算

mathモジュールのドキュメントでは、複素数(complex numbers)を扱うときにはcmathモジュールを使うことを求めています、cmathモジュールは“Mathematical functions for complex numbers”と説明されているので、cmathの”c”はcomplexの頭を取っているものと思われます。

  1. #4 cmathモジュールによる極形式の計算
  2. import cmath
  3. import math
  4. zc=1+cmath.sqrt(3)*1j
  5. print(abs(zc))
  6. print(cmath.phase(zc))
  7. print(cmath.phase(zc)/cmath.pi)
  8. print(cmath.phase(zc)/cmath.pi*180)
  9. print(math.degrees(cmath.phase(zc)))
  10. print(cmath.polar(zc))
  11. print(cmath.rect(2, cmath.pi/3))

1.9999999999999998
1.0471975511965976
0.3333333333333333
60.0
59.99999999999999
(1.9999999999999998, 1.0471975511965976)
(1.0000000000000002+1.7320508075688772j)

  1. 4行目のようにcmathモジュールでも複素数の変数を定義するときは、虚部をjとして表現します。
  2. cmathモジュールには絶対値を単独で計算する関数はありません。5行目のように組み込み関数のabs関数で絶対を計算しています。
  3. 6行目のように、phase関数で偏角をradianで計算することができます。
  4. 7行目のように、radianで計算した偏角を$pi$で割ると$\pi/3$であることがわかります。
  5. 8行目のように、上記の数値に180を掛けると弧度法で計算した偏角を求めることができます。
  6. 9行目では7,8行目をdegree関数でまとめて計算しています。結果はほぼ同じですが小数点以下で誤差が生じてしまいます。
  7. 10行目のように、polar関数を使うと、絶対値と偏角をタプルで計算することができます。
  8. これまでの逆で11行目のように、rect関数に絶対値、偏角を引数として渡すと実部と虚部がタプルで返されます。なぜか、実部も少し誤差が発生し、$\sqrt{3}i$も小数点以下の表記となります。

SymPyモジュールによる複素数の定義と絶対値の計算

SymPyモジュールでは、虚数単位は大文字のIで表し、複素数の計算をします。

  1. #5 sympyモジュールによす複素数の定義と絶対値の計算
  2. import sympy
  3. import numpy as np
  4. zs=3+4*sympy.I
  5. display(abs(zs))
  6. display(np.abs(zs))
  7. display(sympy.Abs(zs))

5
5
5

  1. 4行目のようにSymPyモジュールでは、変数は虚数単位Iを使って複素数を定義します。
  2. 5行目のように絶対値は、組み込み関数のabs関数を使って計算することができます。
  3. 6行目のようにNumPyモジュールのabs関数で同様に計算することができます。
  4. 7行目のように、SymPyモジュールでは大文字のAからはじまるAbs関数（大文字を使って他のモジュールと関数名の重複を避けるのはSymPyモジュールではよくあることです。）で計算することができます。
  5. 機能が豊富なSymPy関数ですが、複素数の偏角などを求める関数を見付けることができません。