Pythonでフィボナッチ数列を計算する

Pythonでフィボナッチ数列を計算します。

フィボナッチ数列の基本的な計算方法

定義通りフィボナッチ数列を計算する

最もシンプルな方法によるフィボナッチ数列の計算

フィボナッチ数列は次の式で与えられる数列です。

F0 = 0,

F1 = 1,

Fn = Fn-1 + Fn-2 (n ≥ 0)

定義通りの方法で100以下のフィボナッチ数列を計算します。

  1. #1 定義通りの方法でn以下のフィボナッチ数列を計算する
  2. a, b = 0, 1
  3. while b < 100:
  4. print(b, end=' ')
  5. a, b = b, a+b

1 1 2 3 5 8 13 21 34 55 89

$a=F_1$、$b=F_2$からはじめ、whileループで$a$に$F_2$を代入し、bに$F_1+F_2$を計算して代入することを同時に行うのが4行目です。昔のプログラミング言語では、tempのような変数を定義し、次のようにする必要がありました。

temp = b

b = a+temp

a = temp

フィボナッチ数列を関数でリストとして返す

#1のプログラムを$F_1$から$F_{10}$までというように、n個のフィボナッチ数列のリストにして戻す関数に作りかえます。

  1. #2 n番目までのフィボナッチ数列をリストにする関数
  2. def fib_l(cnt):
  3. a, b = 0, 1
  4. fib_l=[]
  5. while cnt:
  6. cnt-=1
  7. fib_l.append(b)
  8. a, b = b, a+b
  9. return fib_l
  11. fib_l(10)

[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]

fib_lというリストを定義し、引数cntに対し値を計算するごとにリストに追加するとともに、cntを1つずつ減らします。while cnt:となっているので、cntが0になったらループから抜けて、戻り値としてリストを返します。

再帰関数を使いフィボナッチ数列を計算する

再帰関数でn番目のフィボナッチ数列を計算する

再帰関数を使ってフィボナッチ数列を計算することができます。

  1. #3 再帰関数でn番目のフィボナッチ数列を計算する
  2. def fib_r(seq):
  3. if seq <= 1:
  4. return seq
  5. return(fib_r(seq-1) + fib_r(seq-2))
  7. fib_r(10)

結果は55となり正しく計算されています。

フィボナッチ数列の定義、$F_n = F_{n-1} + F_{n-2}$を表現したのが5行目です。fib_r(seq)が実行されるとすぐに5行目に入りfib_r(seq-1)を呼び出し、最初の関数の実行が一時中断されます。同様にfib_r(seq-2)、 fib_r(seq-3)とfib_rがseqの値を減らしながら呼び出した関数の処理を中断して次々と実行されます。seqが2として実行されると5行目fib_r(1)とfib_r(0)は、3行目のif節に入るので、戻り値としてそれぞれ1,0を返します。関数fib(2)は戻り値を返して終了すると、反転してこれまで中断されていた関数が次々と値を返していきます。最終的に、定義通り1つ前と2つ前の数値を足し上げていきます。

再帰関数の過程を詳しく見る

この数式はフィボナッチ数列の定義をそのまま表していますが、これでなぜ正しく計算できるのか次の3か所にprint文を入れて検証します。

1 関数に入った時に引数seqをptint

2 if文で関数を抜けるときの戻り値をrtnとして戻す

2 2つの関数の合計を返り値としてrtnとして戻す

また、実行順番を示すためiをカウンタとして同時に表示します。

  1. #4 再帰関数でn番目のフィボナッチ数列を計算する
  2. def fib(seq):
  3. global i
  4. i+=1
  5. print('#'+str(i),'fibに入る時 seq=',seq)
  6. if seq <= 1:
  7. i+=1
  8. print('#'+str(i),'１つ目のreturn=',seq)
  9. return seq
  10. rtn=fib(seq-1) + fib(seq-2)
  11. i+=1
  12. print('#'+str(i),'２つ目のreturn=',rtn)
  13. return rtn
  15. i=0
  16. fib(4) 

#1 fibに入る時 seq= 4
#2 fibに入る時 seq= 3
#3 fibに入る時 seq= 2
#4 fibに入る時 seq= 1
#5 １つ目のreturn= 1
#6 fibに入る時 seq= 0
#7 １つ目のreturn= 0
#8 ２つ目のreturn= 1
#9 fibに入る時 seq= 1
#10 １つ目のreturn= 1
#11 ２つ目のreturn= 2
#12 fibに入る時 seq= 2
#13 fibに入る時 seq= 1
#14 １つ目のreturn= 1
#15 fibに入る時 seq= 0
#16 １つ目のreturn= 0
#17 ２つ目のreturn= 1
#18 ２つ目のreturn= 3
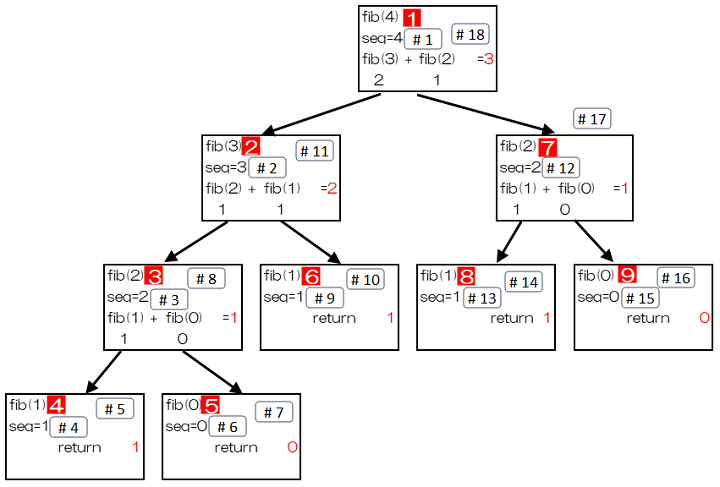
フィボナッチ数列を求める再帰関数
フィボナッチ数列を求める再帰関数

１　関数が実行されると、seq=4(#1)なので10行目の左側のfib(seq-1)がfib(3)となり呼び出されます。右側のfib(seq-2)は、左側のfib(seq-1)が終了し返り値を戻した後に実行されるのでかなり先のことになります。つまり１の実行を保留して２以下が実行されることになります。
２　関数がseq=3(#2)で実行されると１と同様に10行目のfib(seq-1)がfib(2)となり呼び出されます。同じように３(#3)、４(#4)の順に実行されます。
４　関数がseq=1(#4)で実行されると6行目のif文に入り、戻り値として1になり(#5)、３に戻ります。次に10行目の右側がseq=0(#6)で５が実行されます。
５　seq=0なので、6行目のif文に入り戻り値として0(#7)となり、３に戻ります。３ではfib(1)=1とfib(0)=0と結果が出そろい、合計して1(#8)を返り値として２に戻ります。２では10行目の右側から６がseq=1 (#9)で実行されます。
６　seq=1(#9)なので戻り値1(#10)が２に戻ります。２では、３と６の合計2(#11)を１に戻します。１では右側から７がseq=2(#12)が実行されます。
７　seq=2(#12)で呼び出されるので、以下３、４、５と同じ流れが７、８、９で再現されます。結果的に１に７、の返り値1が戻り、２の結果を合計し、最終的にfib(3)＋fib(2)=3(#18)という結果になります。

このように、再帰関数を使うとfib(4)で9回のプログラムが実行されます。プログラミングの練習としては興味深いものがありますが、このままでは実用に耐えるものではありません。

SymPYモジュールによるフィボナッチ数列の計算

フィボナッチ数列は数学的にはとても大切なものなので、当然SymPyモジュールに専用の関数が用意されています。

  1. #5 SymPyモジュールによるフィボナッチ数列の計算
  2. import sympy
  3. fib = sympy.fibonacci(10)
  4. fib

55

$F_{10}$が1から10までの合計と同じ55というのは、ちょっと不思議な感じがします。SymPyモジュールにはn番目の数値を求めるfibonacciしかないので、10番目までをリストで求める場合には次のようにリスト内包表記を使います。

  1. #6 SymPyモジュールによるフィボナッチ数列の計算を配列にする
  2. [sympy.fibonacci(n) for n in range(1, 11)]

[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]

ビネーの公式によるフィボナッチ数列

フィボナッチ数列は漸化式としてとらえると、n番目の数列を一発で求める方法がビネーの公式です。

$F_n = \frac{1}{\sqrt 5}\left(\left(\frac{1\!+\!\sqrt 5}{2}\right) ^n\!-\!\left(\frac{1\!-\!\sqrt 5}{2}\right) ^n\right)$

10番目の値を計算するためには、次の通り実行します。

  1. #7 ビネーの公式によるフィボナッチ数列の計算
  2. seq=10
  3. (((1+5**0.5)/2)**seq-((1-5**0.5)/2)**seq)/(5**0.5)

55.000000000000014

小数点以下で誤差が発生して気持ち悪いので次のように小数点以下を切り捨てる処理を入れた関数を作成します。これを#７のようにリスト内包表記で実行すると次の通りです。

  1. #8ビネーの公式によるフィボナッチ数列の計算を関数にする
  2. def binet(seq):
  3. fib=(((1+5**0.5)/2)**seq-((1-5**0.5)/2)**seq)/(5**0.5)
  4. return int(round(fib))
  6. [binet(n) for n in range(1, 11)]

[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]

結果は正しいようです。