Pythonの小数型で扱うことができる数の大きさ
Pythonで、数値を扱う変数の型の1つとして、浮動小数点型があります。浮動小数点型の変数は、整数だけではなく小数点以下の数字を扱うことができます。浮動小数点型の考え方は非常に複雑で一筋縄ではいかないところがあります。そこで、少しずつその正体に迫っていきます。
浮動小数点型
浮動小数点型の変数の定義
- #1 浮動小数点型の定義
- xi=2
- xf=2.0
- print(xi,type(xi))
- print(xf,type(xf))
22.0
2. 整数を変数に代入すると、4.のように整数型(int)で定義されます。
3. 2.0のように小数点を付けて変数に代入すると、5.のように浮動小数点型(float)で定義されます。
浮動小数点の考え方
コンピュータでは時には10,000,000,000.5のように整数分部の桁数の大きな数値を、またある時は0.12345678のように小数点以下の桁数が多い数値まで、さまざまな数値を扱う必要があります。そこで、数値を表すときに使うbit数が多ければ多いほど、桁数の大きな数値を扱ったり、小数点以下の数値を精度よく計算することができます。
ところで、多くのパソコンは64bitのWindowsやMacOS といったOSを使っています。これは、64bitのデータを一つカタマリとして分割されずに処理することができることを指しています。よって、数値を64bitの中で表現することができれば効率が良く処理することができます。
このように、少しでも精度良く計算したいという要求と64bit以内で数値を表現したいという相反する要求がありますが、これらを両立させるのが浮動小数点方式という考え方です。つまり、小数点の位置を固定してしまうと、64bitで表すことができる数字の範囲が限定されてしまいます。そこで、数字の大きさに合わせて小数点の位置を柔軟に移動(つまり浮動)させることで、限られた64bitの中でいろいろな大きさの数字をうまく表現しようとするものです。
ところで、少し前までは多くのパソコンは32bitOSを使っていました。そこでは数値を32bitで表現する方法を採っていましたが、浮動小数点方式はこのときの仕組みが基本となっています。前述のとおり、現在は64bitOSが主流となりつつあるのでその倍のbit数を使い数値を表せるようになりました。このことから以前より精度よく、数値を表現できることができるようになりました。この仕組みを倍精度浮動小数点方式といい、Pythonではこの倍精度浮動小数点で数値を表現することを基本としています。
浮動小数点の計算
具体的な浮動小数点の計算
いろいろな数値を2進数に変換したものを表にまとめました。
| 10進数 | 2進数 | 正規化した2進数 |
|---|---|---|
| 3 | 11.0 | $1.1×2$ |
| 50 | 110010.0 | $1.10010×2^6$ |
| 100 | 1100100.0 | $1.100100×2^6$ |
| 9999 | 10011100001111.0 | $1.0011100001111×2^{13}$ |
| 0.5 | 0.1 | $1×2^{-1}$ |
| 0.625 | 0.101 | $1.01×2^{-3}$ |
9999程度の数字でも整数部分で14桁を使ってしまいます。一方、小数点以下で桁数を多く使うものもあります。前述のように小数点を固定すると、表現できる数字の大きさや精度が限られてしまうので、正規化という考え方を使い小数点の位置を合わせるようにします。正規化された値は表の一番右側の列になります。
正規化の考え方
正規化について、もう少し具体的に考えます。例えば、50と100を比べると図の通りになります。
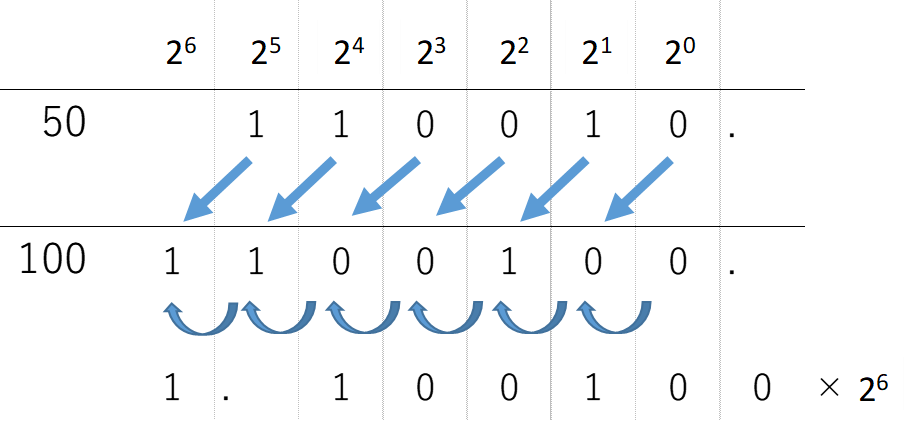
ここで
$50=2^5+2^4+2^1$
$100=2^6+2^5+2^2$
となるので、50の1と0の並びを左側にシフトし最後の桁に0を補うと、すべての項が2倍になるので、100になります。逆に100を右側に1桁シフトすると50になります。このように、ビット全体を左にシフトすると2倍に、右側にシフトすると1/2倍になります。このことから、小数点を表すときには、はじめの1からはじまる数字と、1.XXXというように1からはじまるようにビットをシフトし、シフトした桁数を別の場所に控えておく必要があります。ここで、正規化された1と0の組合せを仮数部といい、移動したビット数を指数部といいます。また、数値には正と負があるので、これを区別するために符号部として1bit使用します。
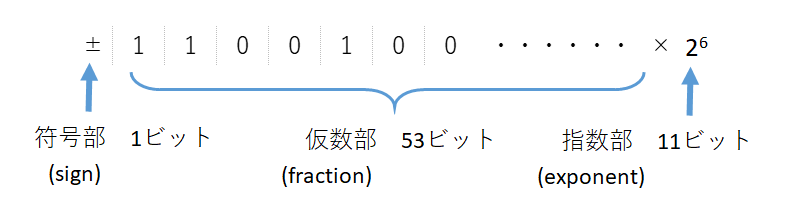
まず、仮数部の計算を簡単のため整数の値を計算します。このとき、どれくらいの大きさの数値まで計算できるのかを調べてみます。
仮数部を2bitとした場合、0(00)1(01)2(10)3(11)の4通りで、最大3までを表現することができます。このように、2進数では最大$2^{bit数}-1$まで計算することができます。このため、倍精度浮動小数点の53bitでは、仮数部は最大$2^{53}-1=9,007,199,254,740,991.0 $約9000兆になります。そこで、$f52=2^{52}-1=4503599627370495、f53=2^{53}-1=9007199254740991、f54=2^{54}-1=18014398509481983$を定義します。
- #3 倍精度浮動小数点で表すことができる整数の大きさ
- f52=4503599627370495.0
- f53=9007199254740991.0
- f54=18014398509481983.0
- print(f'2^52-1={f52:>20.1f} \n 2^52+0.5={f52+0.5:>20.1f} : 2^52+1.0={f52+1.0:>20.1f}')
- print(f'2^53-1={f53:>20.1f} \n 2^53+0.5={f53+0.5:>20.1f} : 2^53+1.0={f53+1.0:>20.1f}')
- print(f'2^54-1={f54:>20.1f} \n 2^54+0.5={f54+0.5:>20.1f} : 2^54+1.0={f54+1.0:>20.1f}')
2^52-1= 4503599627370495.0 2^52+0.5= 4503599627370495.5 : 2^52+1.0= 4503599627370496.0 2^53-1= 9007199254740991.0 2^53+0.5= 9007199254740992.0 : 2^53+1.0= 9007199254740992.0 2^54-1= 18014398509481984.0 2^54+0.5= 18014398509481984.0 : 2^54+1.0= 18014398509481984.0
4. $2^{52}-1$の付近であれば0.5や1.0との和も問題なく計算されます。
5. $2^{53}-1$の付近になると1.0との和は問題なく計算されますが0.5との和は小数点以下が切り上げられてしまいます。
6. さらに$2^{54}-1$の付近になると、整数1桁目で誤差が発生します。このことから$2^53-1$を超えると、大体は正しく計算されますが、整数部分の小さな部分や小数点の部分で誤差が生じるようになってしまいます。
$2^{53}±10$の具体的な計算
さらに、$2^{53}±10$の範囲でどのように計算されるか細かく見ていきます。
- #4 浮動小数点での2^53±10の計算
- f53=9007199254740991.0
- for i in range(-10,0):
- print(f'2^53-1{i:>3}={f53+float(i):>20.1f}')
- for i in range(11):
- print(f'2^53-1+{i:>2}={f53+float(i):>20.1f}')
2^53-1-10= 9007199254740981.0 2^53-1 -9= 9007199254740982.0 2^53-1 -8= 9007199254740983.0 2^53-1 -7= 9007199254740984.0 2^53-1 -6= 9007199254740985.0 2^53-1 -5= 9007199254740986.0 2^53-1 -4= 9007199254740987.0 2^53-1 -3= 9007199254740988.0 2^53-1 -2= 9007199254740989.0 2^53-1 -1= 9007199254740990.0 2^53-1+ 0= 9007199254740991.0 2^53-1+ 1= 9007199254740992.0 2^53-1+ 2= 9007199254740992.0 2^53-1+ 3= 9007199254740994.0 2^53-1+ 4= 9007199254740996.0 2^53-1+ 5= 9007199254740996.0 2^53-1+ 6= 9007199254740996.0 2^53-1+ 7= 9007199254740998.0 2^53-1+ 8= 9007199254741000.0 2^53-1+ 9= 9007199254741000.0 2^53-1+10= 9007199254741000.0
$2^{53}$までは正しく計算されますが、これを超えると整数分部第1位が偶数になり不規則に変化します。このあたりは、とても不思議なところです。
切り捨てられるbitの丸め
浮動小数点で切り捨てられるbitの処理方法は丸め処理というものを行っています。
- for i in range(10):
- xdec=2**53+i
- xbin=base_dec2bin(xdec)
- if xbin[52:]=='11':
- ydec=(base_bin2dec(xbin[:53])+1)*2
- else:
- ydec=base_bin2dec(xbin[:53])*2
- print(xdec,xbin,float(xdec))
9007199254740992 100000000000000000000000000000000000000000000000000000 9007199254740992.0
9007199254740993 100000000000000000000000000000000000000000000000000001 9007199254740992.0
9007199254740994 100000000000000000000000000000000000000000000000000010 9007199254740994.0
9007199254740995 100000000000000000000000000000000000000000000000000011 9007199254740996.0
9007199254740996 100000000000000000000000000000000000000000000000000100 9007199254740996.0
9007199254740997 100000000000000000000000000000000000000000000000000101 9007199254740996.0
9007199254740998 100000000000000000000000000000000000000000000000000110 9007199254740998.0
9007199254740999 100000000000000000000000000000000000000000000000000111 9007199254741000.0
9007199254741000 100000000000000000000000000000000000000000000000001000 9007199254741000.0
9007199254741001 100000000000000000000000000000000000000000000000001001 9007199254741000.0
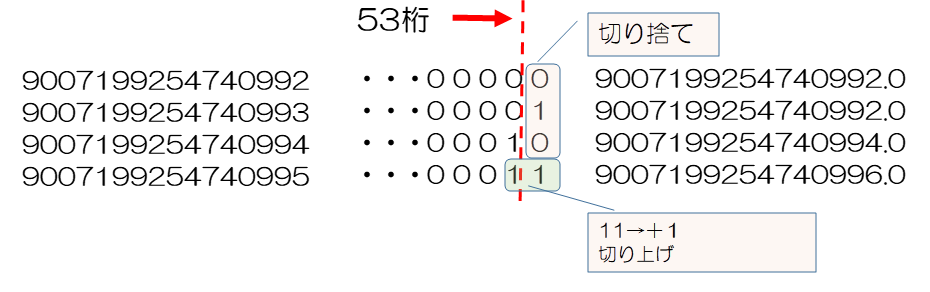
倍精度浮動小数点で$2^{53}$以上の数値は54bit以上になります。そこで、53bitの仮数部に収めるために、最後の1桁を省略し、指数部の方に1bitシフトしたことを記録しておきます。このたき、最後の1桁が1のとき、すべて切り捨ててしまうと、全体的に少しだけ数字が小さくなる傾向になってしまうので、最後の2桁が11の場合は1だけ切り上げるようにしてバランスを取ります。
つまり、最後の2桁が”00”、”01”、”10”の場合は最後の桁を切り捨て、”11”の場合は下二けた目を切り上げます。このように、53bitに収まらない部分は丸められるので、少しだけ誤差は発生するもののおおまかな数値としては正しく計算されます。
指数部の計算
正規化とビットのシフト
指数部の計算の考え方
指数部は、仮数部を正規化するときに何ビットだけシフトしたかを表します。ところで、浮動小数点では、0.25のように1より小さい数値を扱うときには右、つまりマイナスの方向にシフトすることがあります。このため、指数部は1023を足し合わせて計算します。この1023をバイアス値(偏り)いい、またバイアス値を使った計算方法を下駄ばき表現、オフセット・バイナリ (offset binary)といいます。
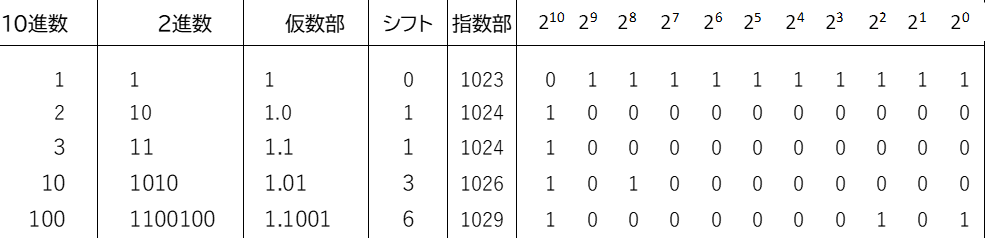
10進数で1は2進数で1となるので、仮数部も1となりシフトする必要はありません。つまり指数部は0になるので、バイアス値は1023($2^{10}-1$)となります。次に10進数の2は2進数で”10”となり、正規化すると仮数部は1.0となり1bitシフトする必要があります。このため、バイアス値は1024(1023+1)となります。同様に10進数の100を2進数にすると”1100100”となるので、正規化され仮数部は1.1001で6bitシフトする必要があります。このためバイアス値は1029(1023+6)となります。
Pythonで10進数を2進数の仮数部と指数部に変換する
- #2 分数を定義通り2進数に変換
- def base_dec2bin(dec):
- nary = ''
- while dec > 0:
- nary = str(dec % 2) + nary
- dec //= 2
- return nary
- def ieee(dec):
- nary=base_dec2bin(dec)
- frac='1.'
- for i in range(1,len(nary)):
- frac+=nary[i]
- bias=len(nary)-1+1023
- return frac,nary,bias,base_dec2bin(bias)
- for i in range(1,101,10):
- frac,nary,bias,expon=ieee(i)
- print(f'{i:>3} {nary:<10} {frac:<10} {bias:<4} :{expon}')
2. base_dec2binでは10進数を2進数に変換します。
4. whileループの中で10進数を次々に2で割り、余りをnaryを右からつなげていきます。この結果naryに2進数に変換された値が文字列で代入されます。
9. ieeeでは、10進数を2進数の仮数部と指数部に変換します。
10. base_dec2binにより10進数の数値を2進数の文字列にしてnaryに代入します。
11. fracに”1.”、を代入し、それ以降2桁目以降をfracに代入します。
14. biasにはnaryの桁数-1+1023でバイアス値を計算します。
20. 1から10おきに10進数、2進数、仮数部、指数部とバイアス値とその2進数にした値を出力します。
