Pythonでの割り算と小数の計算
四則演算のうち割り算の計算をご紹介します。割り算は割り切れないのが通常で、余りを計算するか、または小数点第何位で切り捨てるかということを考える必要があります。このように、割り算や小数点以下の数値を扱う計算をする場合は、細かい部分に気を配る必要が生じます。。
Pythonによる四則演算
Pythonによる割り算
足し算との比較
Pythonでの足し算と割り算は次の通りになります。
- #1 Pythonでの割り算の計算
- print(20+4)
- print(20/4)
24 5.0
2行目のように整数20と整数4の足し算の結果は24となり、整数として表示されます。一方、20÷4は整数であるにも関わらず、5.0と少し異なった表示になります。これは、計算結果が小数であることを示しています。このように、割り算の結果はたとえ割り切れたとしても小数として認識されます。
割り算の結果、商と余りの計算
割り算は、/、商は//、余りは%という演算子を使って計算します。
- # 2 python での割り算、商、余りの計算
- x = 20
- y = 3
- print(f'x / y = {x/y}')
- print(f'x // y = {x//y}')
- print(f'x % y = {x%y}')
x / y = 6.666666666666667 x // y = 6 x % y = 2
3. 割り切れない場合は、16~17桁を表示し、一番下の桁は四捨五入されます。
4. ”//”を使うと商、つまり割り切れない場合は小数点以下が切り捨てられ整数表示されます。
5. ”%”を使うと、割り切れない場合は余りが表示されます。この場合も、結果は整数として表示されます。
変数を使った割り算
変数を使って割り算をしても結果は同じです。
割る数も割られる数も正の場合
割られる数をdividend、割る数をdivisorとすると、割り算はdividend / divisorで計算します。また、余りを考えずに割った結果はresult、余りを考える場合、商はquotient、余りをremainderとします。
- #3 Pythonでの割り算の計算
- dividend = 20
- divisor = 3
- result = dividend / divisor
- print(f'result = dividend / divisor={result}')
- quotient = dividend // divisor
- print(f'quotient = dividend // divisor={quotient}')
- remainder = dividend % divisor
- print(f'remainder = dividend % divisor={remainder}')
- print(f'remainder = dividend-quotient*divisor={dividend-quotient*divisor}')
result = dividend / divisor=6.666666666666667 quotient = dividend // divisor=6 remainder = dividend % divisor=2 remainder = dividend-quotient*divisor=2
4. 通常、割り算は”/”を使い、少数点表示となり割り切れないときは、JupyterNotebookでは有効桁数(整数部分と小数部分を合わせて)17桁程度で、最後の桁は四捨五入して表示されます。
6. 商(小数点以下を切り捨て)を求めるときは、”//”を使います。
8. 商を求めた際の余りは”%”を使います。余りは次の式で計算されます。
10. 3.の結果を検証しています。
割られる数がマイナスの場合
割られる数がマイナスの場合の考え方をご紹介います。
- #4 Pythonでの割り算の計算
- dividend = -16
- divisor = 3
- result = dividend / divisor
- print(f'result = dividend / divisor={result}')
- quotient = dividend // divisor
- print(f'quotient = dividend // divisor={quotient}')
- remainder = dividend % divisor
- print(f'remainder = dividend % divisor={remainder}')
- print(f'remainder = dividend-quotient*divisor={dividend-quotient*divisor}')
result = dividend / divisor=-5.333333333333333 quotient = dividend // divisor=-6 remainder = dividend % divisor=2 remainder = dividend-quotient*divisor=2
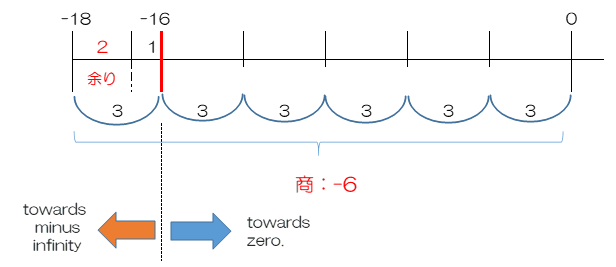
- 4行目のように単純な割り算では結果は-5.33・・・3となり、5行目のように小数点以下を切り捨てた場合、図の通りマイナス無限大方向(towards minus infinity)に切り捨てられ、-6になります。
- 6行目での余りの計算においては、マイナス無限大方向に切り捨てられた、$-18(3\times(-6))$を基準として、割られる数-16との差を取り、2になります。
- これらの関係は前の式、$余り(remainder))=割られる数(dividend:)-商(quotient)×割る数(divisor)$と同じです。
小数点以下の桁数を設定する
10÷6にように割り切れない割り算をする場合、”.1f”,”.2f”とすると小数点第1位、第2位のように表示桁数を指定することができ、一番下の桁数は四捨五入されます。
- #5 小数点以下の桁数の設定
- num=10/6
- print(f'整数表示:{num:.0f} 小数点第1位:{num:.1f} 小数点第2位:{num:.2f}')
整数表示:2 小数点第1位:1.7 小数点第2位:1.67
計算結果を整数表示にする
今度は消費税10%を考慮するため、税抜価格を1.1倍するプログラムを作成します。
- #6 計算結果を出力する
- price=1000
- print(f'本体価格は{exclude:,}円、税込み価格は{exclude*1.1:,}円です')
- include=1000*1.1
- print(f'本体価格は{exclude:,}円、税込み価格は{include:,}円です')
本体価格は1,000円、税込み価格は1,100.0円です 本体価格は1,000円、税込み価格は1,100.0円です
税込み金額の計算では税抜価格を1.1倍しているので、税込み価格は小数として解釈され1,100.0円という変な表示になってしまいます。そこで、波括弧の中で小数点以下の桁数を設定します。“.0f”は小数点以下0桁を表示することを示しています。
小数でも整数表示にする
- #7 小数点以下の出力をする
- price=1000
- tax=1000*0.1
- include=price+tax
- print(f'税抜き価格は{price:,.0f}円、税金は{tax:,.0f}円、税込み価格は{include:,.0f}円です')
本体価格は1,000円、税金は100円、税込み価格は1,100円です
このように、計算結果をどのように表示するかを併せて設定することができます。また、式が煩雑になる場合には、あらかじめ変数に書式付きの文字列を代入し、print関数を使い出力することもできます。
- #8 あらかじめ変数に書式付きの文字列を代入してから出力
- price=1000
- text=f'税抜き価格は{price:,.0f}円、税金は{tax:,.0f}円、税込み価格は{include:,.0f}円です'
- print(text)
本体価格は1,000円、税金は100円、税込み価格は1,100円です
小数に関わる計算
Pythonでプログラミングをしていて、最も戸惑うものの一つとして少数の計算があります。細かいところで誤差が発生したり、十分な桁数まで計算してくれないことがあるためです。
小数の計算での誤差や表示桁数
次の例の場合に問題が生じます。
- #9 小数の計算
- print(10/3)
- print(1.2+1.2+1.2)
- print(1.1+1.1+1.1)
- print(1/81)
3.3333333333333335 3.5999999999999996 3.3000000000000003 0.012345679012345678
- 2行目のように10/3の場合、3.33・・と永遠に3が続きます。ところがPythonでは小数点以下16桁まで表示され、最後の桁はなぜか5と2だけ切り上げられます。
- 3行目のように1.2を3回足すと3.6より少しだけ小さくなります。逆に4行目のように1.1の場合は3.3より少しだけ大きくなります。
- 5行目のように、1/81は何か面白い結果になりそうですが、いいところで終わってしまいます。
小数の表示の問題点の解決法
上記のように小数点以下で誤差が発生しますが、小数点以下16桁くらいのレベルなのでほとんどの場合、問題になることはありません。表示桁数を限定することできれいに表示されます。逆に表示桁数を増やすこともできます。
- #10 小数点以下の誤差が生じる場合の表示
- print(f'{10/3:.5f}')
- print(f'{1.2+1.2+1.2:.1f}')
- print(f'{1.1+1.1+1.1:.1f}')
- print(f'{1/81:.100f}')
3.33333 3.6 3.3 0.0123456790123456783270228243054589256644248962402343750000000000000000000000000000000000000000000000
- 2行目のように、”.5f”として小数点以下5桁目までの表示に限定することができます。
- 同じように3行目、4行目のように1桁までの表示に限定することができます。このとき、コンピュータの内部ではもっと下の桁数までの値を把握していますが、これをprint関数で表示の桁数を限定しているだけですが、通常の場合、ほとんどの場合問題になることがありません。
- 5行目のように、”.100f”とすると桁数を増やすことができますが、小数点以下54桁程度となり、それ以降は0となってしまいます。割る数の81は3の倍数なので割り切れることは考えられないので、コンピュータの内部で把握できる桁数は限りがあることがわかります。
フォーマット済み文字列リテラルやこれまでの数値演算のまとめ
数を表すフォーマット済み文字列リテラル
これまで取り上げたフォーマット済み文字列リテラルは次の通りです。
| 書式の記号 | 効果 |
|---|---|
| d | 整数 |
| , | 3桁表示 |
| .数字f | 小数点以下の表示桁数 |
| .数字g | 有効桁数 |
- #11 小数点以下の桁数を指定する
- print(f'{1.2+1.2+1.2:.1f}')
- print(f'{1000/3:.5f}')
- print(f'{1000/3:.5g}')
- print(f'{1/81:.100f}')
- print(f'{1/81:.100g}')
3.6 333.33333 333.33 0.0123456790123456783270228243054589256644248962402343750000000000000000000000000000000000000000000000 0.012345679012345678327022824305458925664424896240234375
- 2行目のように”:数字f”を指定すると小数点以下の桁数を指定することができます。
- 3行目のように” :数字g”を指定すると整数部分も含めて指定した桁数を表示します。このような指定の方法を有効桁数といいます。
- 4行目に100桁まで指定すると、少数点以下54桁程度まで計算しそれ以降は0となります。
- 5行目のように有効桁数を100桁とすると、計算ができる桁数までに限って表示される。
数字の表示の桁数と幅、左右、中央揃えを指定する
フォーマット済み文字列リテラルでは、数字などを表示する幅や左詰め、右詰め、中央揃えといった設定もすることができます。
| 書式の記号 | 効果 |
|---|---|
| <+数字 | 左揃え、数字で指定した桁数 |
| >+数字 | 右揃え、数字で指定した桁数 |
| ^+数字 | 中央揃え、数字で指定した桁数 |
- #12 数字の表示の桁数と幅、左右、中央揃えを指定する
- print(f'{3000:<20d}')
- print(f'{3000:^20,}')
- print(f'{3000:>20,}')
- print(f'{0.011:<20.2f}')
- print(f'{0.016:^20.2f}')
- print(f'{0.019:>20.1f}')
3000
3,000
3,000
0.01
0.02
0.0
- 2行目のように数字3000に対し、20文字分の幅の左揃えになります。このとき数字の種類は”d”なのでカンマ無しの整数として表示されます。
- 3行目のように数字3000に20文字分の幅の中央揃えになります。このとき数字の種類は”,”なのでカンマ付きの整数として表示されます。
- 4行目のように同じ数字が20文字分の幅の右揃えになります。
- 5行目のように0.011は”.2f”となるので、小数点第2桁まで表示されます。
- 6行目のように0.016は”.2f”となるので、小数点第2桁まで表示されます。このとき、小数点3桁目で四捨五入されていることがわかります。
- 7行目のように0.019は”.1f”となるので、小数点第1位まで表示されます。
数値の表の桁数や幅を変数で指定する
これまで、フォーマット済み文字列リテラルの値を数値で直接指定しましたが、実は変数を使って動的に指定することもできます。この場合には、変数は{}中括弧で囲むようにします。
- #13 数字の表示の桁数や幅を変数で指定する
- width=10
- digits=3
- print(f'{0.01234:^20.2f}')
- print(f'{0.01234:^{width}.2f}')
- print(f'{0.01234:^20.{digits}f}')
- print(f'{0.01234:^{width}.{digits}f}')
0.01
0.01
0.012
0.012
5. 数値を表示する幅をwidthに代入した変数で指定しています。
6. 小数点以下の桁数をdigitsに代入した変数で指定しています。
7. 幅と桁数を変数で指定しています。
四則演算
ようやく四則演算がそろいました。これまで取り上げた四則演算は次の通りです。
| 演算 | 記号 | 概 要 |
|---|---|---|
| 和 | + | 足し算 |
| 差 | - | 引き算 |
| 積 | * | 掛け算 |
| べき乗 | ** | べき乗 平方根はx**0.5で計算 |
| 割り算 | / | 割り算で割り切れない場合は有効桁数17桁程度まで表示 |
| 商 | // | 割り算の結果小数点以下を切り捨て |
| 余り | % | 割り算で賞を求めた時の余り |