回帰分析をするため散布図を描き、回帰直線を引く
あなたは広報部に在籍し、広告の効果を検証する仕事をしているとします。1か月あたりの広告の件数と新規の顧客数の関係を分析し、広告の効果があったかどうかを分析するとともに、新規顧客数を的確に予測し、過不足なく商品を用意することが求められています。このような場合に、回帰分析という手法がとても有効です。ほかにも、回帰分析には次のような使い方が想定されます。
- かき氷屋さんが気温と売上の関係を分析して、天気予報を見ながら明日、用意する氷の量を決め売り切れや売れ残りを防ぐ。
- 開発した血圧を下げる薬は本当に効果があるのか。また効果がある場合、血圧を基準値に戻すためにどれだけ投与すればよいかを分析し、治療効果を上げる。
- ある企業の今月の売上高から3か月後の株価を予測し大儲けしたい。
このように、回帰分析は幅広い分野で活用する強力なツールです。
散布図で2つの数値の関係を表現する
広告件数と新規顧客数という2つの量を考えます。回帰分析では、広告件数のように自分で量を決めたり、あらかじめデータを入手できたりする量を説明変数、新規顧客数のように広告件数に応じて量が変化すると考えられ、より成果を上げるために正確に予測したい量を目的変数といいます。前の例では、気温、薬の投与量、今月の売上は説明変数、かき氷の売上、血圧、株価は目的変数です。
図表1は、ここ数か月の広告件数と新規顧客数の関係を示しています。この表から、広告件数と新規顧客数の関係を読み解きます。
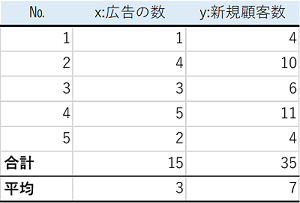
全体像をつかむために散布図というグラフを描きます。通常、説明変数:$x$を横軸、目的変数:$y$を縦軸に取り、それぞれの組み合わせの座標(場所)に点をプロットします。プロットとは、点を打っていくことをいいます。
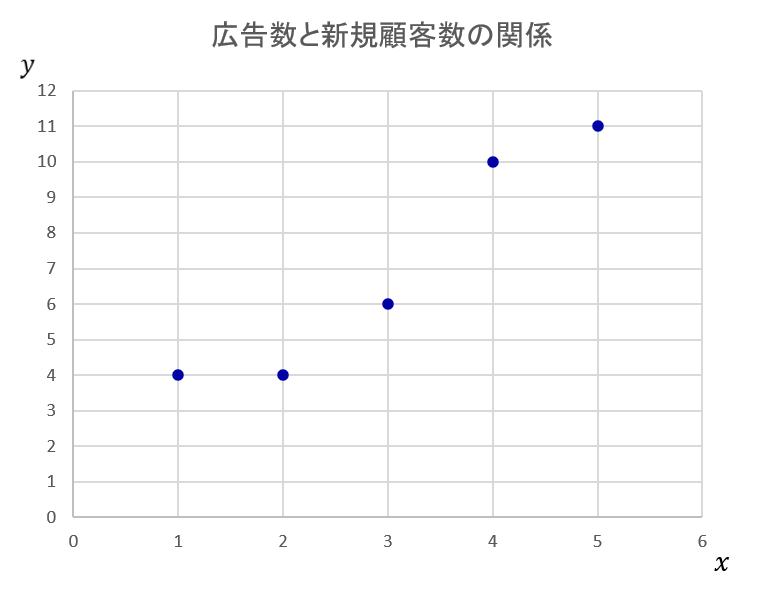
散布図を見ると、広告件数が増えるとそれに応じて新規顧客数が増加していることがわかります。このように2つの量の間に明確な関連がみられる場合、相関関係にあるといいます。
回帰直線を引く
散布図に$x$と$y$ の関係を示す直線を引くと、より的確に相関関係を把握することができます。このような直線を回帰直線といいます。それでは、グラフに回帰直線を引いてみます。
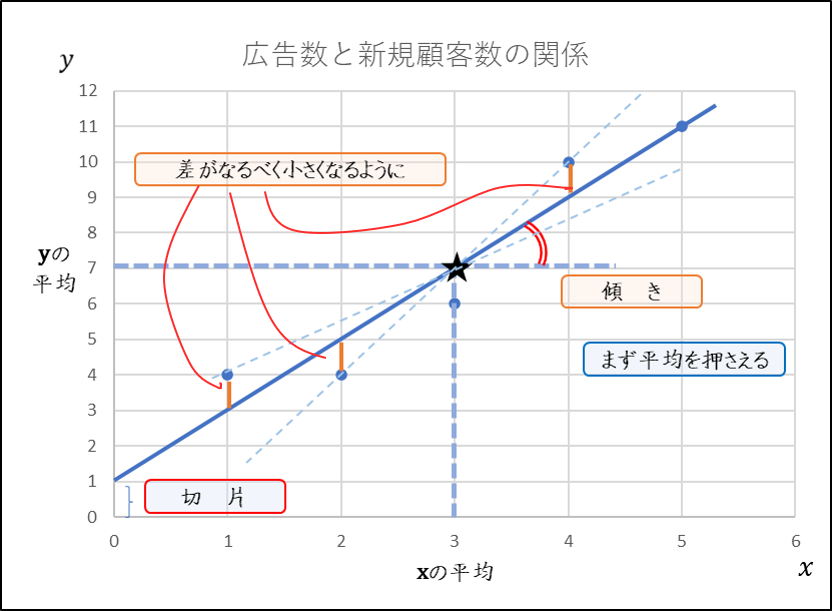
この例は相関関係が明らかな部類に入りますが、それでも線を引くときには少し戸惑うと思います。それでは、どのようにすれば、うまく回帰直線を引くことができるでしょうか。
はじめに$x$と$y$の平均を求めます。平均は各変数の中心となる値なので、回帰直線は$x$と$y$の平均の組み合わせの座標(★)を通ると考えられます。次に、$x$の平均と$y$の平均の点を中心に直線の傾き(角度)を調整して、回帰直線が点のカタマリの中間をうまく突っ切るように、つまり各点との距離の合計がなるべく小さくなるような線を引きます。このようにすると、精度の高い回帰曲線を描くことができます。
回帰直線を数式にする
回帰直線を描いたら今度は数式で表現します。この式を、回帰式といいます。この例では$x$が1増えると$y$が2増えるので傾きは2です。また、回帰直線と$y$軸との交点、つまり$x$が0のときの$y$の値を切片といます。ここでは切片は1です。回帰分析では傾きを$\beta$、切片を$\alpha$とすることが多く、$\beta$=2、$\alpha$=1となります。この結果、回帰直線は次の通りになります。
回帰直線を表す回帰式
回帰直線をあらわす式を作ることにより、次のような予測ができます。
- 広告の件数(説明変数$x$)と新規顧客数(目的変数$y$)には強い相関関係があり、広告には一定の効果がある。
- もし、4件の広告を打つとすると$x=4, y=1+2x$から$y=9$となり、9件の新規顧客が見込める。
このように、広告の効果があったのか、また何件の広告を打つのが最も効果的なのか、根拠をもって答えることができるようになります。
まとめ
散布図による回帰分析を使うと、2つの量の相関関係を調べることができます。散布図を描くことは回帰分析の基本ですが、目分量で回帰直線を引くと人によって結果がまちまちになっています。このため、数式を使って式を推定する必要があり、この計算をするためには、分散、共分散という言葉の理解が必要です。
今回は、1つの説明変数で相関関係を説明することができました。ところが現実には2つ以上の説明変数を使わないとうまく説明できない場合がほとんどです。そうなると、関係が複雑すぎて散布図だけではうまく分析することはできません。数式を使ってすっきりと分析する方法が必要になります。この場合、重回帰分析が有効です。