分散と共分散の簡便な計算方法
分散や共分散の計算は、はじめに平均を求め、その平均と各データの偏差を求めていかなければならないので思いのほか複雑です。そこでもっと簡単に計算する方法を探ってみます。
分散の簡便な計算方法
まず、定義通りの計算方法を振り返りながら、簡便法により計算します。
分散の簡易計算法
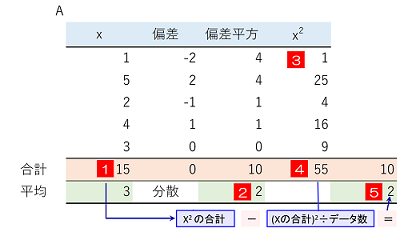
1 定義通りの方法で計算するため$x$の合計と平均を計算
2 偏差平方($x$と平均の差の2乗)を合計して偏差平方和を求め、データ数(ここでは5)で割ることにより分散を計算。ここでの結果は2になる。
3 簡便法で計算するため各データ$x$の2乗を計算
4 3で求めた$x$の2乗を合計
5 4で求めた数字から、データ$x$の合計を2乗してデータ数で割った数字を差し引く。この結果が偏差平方和となり、偏差平方和をデータ数で割ることにより分散を計算
確かに2と5で計算した分散の値は一致しています。少しだけ楽になりましたが、あえて簡便法として特筆する必要はないようにも感じます。それでは、次のデータではどうでしょうか。
簡易計算法を使わない
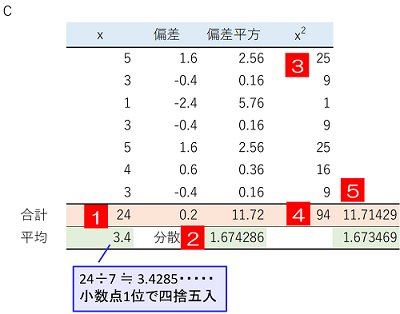
定義通りの方法だと、1の平均の割り算を求める時点で小数点の処理が必要で(ここでは第2位で四捨五入)、以降一つ一つ小数点の計算をする必要があります。ここでは、偏差平方和の11.72を7で割った1.674286が分散になります。一方、簡便法では割り算は最後の5の中の2回で済むので、小数点を含む計算が最小限に抑えることができます。計算の早い段階で小数点の処理をすると、手間がかかる上に、誤差が蓄積され計算結果に影響が出てしまいます。一般的に、割り算は最後に行うのが定石です。
簡便な方法で分散の計算ができる理由
ところで、なぜこの方法で分散が計算できるか、極めてざっくりとしたイメージですが、探ってみたいと思います。
分散の簡易計算法
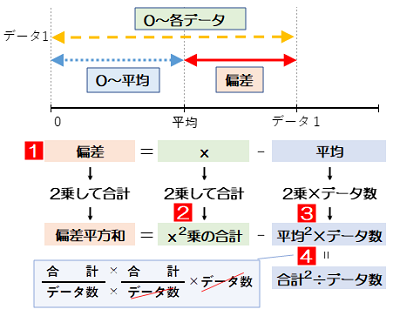
1 偏差=各データ$-$平均 で計算
2 偏差の2乗を合計することに対応して、$x$も2乗して合計
3 平均は同じ大きさなので平均を2乗してデータ数を掛ける
4 偏差平方和=$x$の2乗の合計$-$(平均の2乗×データ数)としてもよいが、小数点の処理の回数を減らすために、平均=合計の2乗÷データ数で置き換える。
繰り返しになりますが、ここでの説明は非常に大雑把ですが、計算方法を直感的に覚える方法としてとらえることができます。大雑把といった理由は2つあります。
- 偏差=$合計-平均$が成り立っても偏差の2乗=合計の2乗$-$平均の2乗は成り立ちません。2乗すると偏差の2乗の方が、(2×合計×平均)だけ大きくなります。
- この図では、平均よりも大きなデータを扱っていますが、平均よりも小さなデータもあります。この場合には偏差=合計$-x$は成り立ちません。
ところが、2つがうまい具合に打ち消しあって、偏差の2乗=合計の2乗$‐$平均の2乗となるのです。この内容の詳しい話は数式を使って証明するしかありません。
共分散の簡易な計算方法
共分散の簡易な計算方法
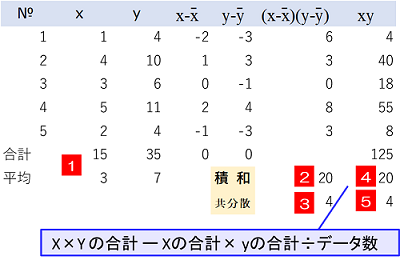
1 定義通りの方法で共分散を求めるため$x,y$の合計と平均を計算
2 $x$の偏差×$y$の偏差を計算して積和を合計
3 2で求めた積和をデータ数で割り、共分散を計算
4 簡便法で共分散を求めるため、$x$×$y$の合計を計算したのち、$x$の合計×$y$の合計÷データ数を差し引き、積和を計算
5 4の積和をデータ数で割って共分散を計算
どちらの方法でも共分散が4となり一致します。なぜ、この方法で共分散を計算することができるのかは、直感的にとらえるのは難しいものがあります。
まとめ
分散、共分散の簡便な計算方法についてイメージをつかむことができました。しかし、厳密には数式を使ってしっかりと証明する必要があります。
共分散の考え方を使うと回帰直線の回帰係数を計算することができます。



