回帰直線の式をPythonで計算する
Pythonを使ってサンプルデータから回帰直線の式を作り、残差や予測値を計算します。はじめに、NumPyを使って積和や偏差平方和を手順通りに計算します。次の特殊な関数や機械学習で使うscikit-learnさらには統計解析で使うstatsmodelsによる方法をご紹介します。
計算の内容
表のサンプルの測定値のデータとして使います。はじめに説明変数を$x$、目的変数を$y$として回帰直線の傾きと切片を求め、ここから元のデータ$x$のそれぞれの値について予測値を計算します。次に、測定値と予測値の残差を計算し、最後にデータ$x$が0および6だった場合の予測値を計算します。
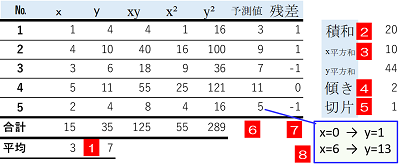
詳しい手順は次の通りです。
なお、全体を通して使う変数は次の通りです。
| 用語 | 変数 | 意味 |
|---|---|---|
| $x$のリスト | $x$ | 説明変数$x$の配列NumPyで計算するのでndarray形式で定義 |
| $y$のリスト | $y$ | 目的変数$y$の配列、ndarray形式で定義 |
| データ | data | 6で代入する$x$の値([0,6]の配列で定義) |
| 平均 | mean | 平均はaverageよりmeanを使うことが多い |
| 偏差平方和 | $T_{xx}$ | 偏差平方和 回帰分析では$T_{xx}$と表現することが多い |
| 積和 | $T_{xy}$ | 積和 回帰分析では$T_{xy}$と表現することが多い |
| 傾き | slope | 回帰直線の式の傾き |
| 切片 | intercept | 回帰直線の式と$y$軸の交点の$y$の値 |
| $x$に対する予測値 | predict_x | $x= [1,4,3,5,2] $に対して計算した予測値 |
| 残差 | resudial_y | $y$の測定値と$x$に対する予測値の差 |
| dataに対する予測値 | predict_d | data=[0,6]に対して計算した予測値 |
NumPyで計算
準備としてサンプルの$x$、$y$および最後に代入するデータをndarray形式で定義します。
NumPyによるデータの定義
- import numpy as np
- x = np.array([1, 4, 3, 5, 2])
- y = np.array([4, 10, 6, 11, 4])
- data = np.array([0, 6])
手順通りの計算
はじめに関数を使わず手順通り計算します。NumPyで使うためで$x,y$を定義し、簡便法を使い積和、偏差平方和を求めたのち、回帰直線の式の傾き、切片を計算します予測値や、残差はNumPyのブロードキャストが使えるのですっきりと表現できます。
最後に0と6の場合を予測する時も、predict_dを求める式に配列を代入すると、配列で答えが返ります。
NumPyを使って簡易法により計算
- n=len(x)
- t_xy=sum(x*y)-(1/n)*sum(x)*sum(y)
- t_xx=sum(x**2)-(1/n)*sum(x)**2
- slope=t_xy/t_xx
- intercept=(1/n)*sum(y)-(1/n)*slope*sum(x)
- print('傾き=',slope,'切片=',intercept)
- predict_x=intercept+slope*x
- print('予測値=',predict_x)
- resudial_y=y-predict_x
- print('残差=',resudial_y)
- predict_d=intercept+slope*data
- print('x=[0,6] --> y=',predict_d)
結果は次の通りです。
傾き= 2.0 切片= 1.0 予測値= [ 3. 9. 7. 11. 5.] 残差= [ 1. 1. -1. 0. -1.] x=[0,6] --> y= [ 1. 13.]
Polyfit関数とpoly1d関数による方法
次にNumPyのpolyfit関数とpoly1dメソッドを使います。これらの概要は次の通りです。polyfit関数の引数に$x$、$y$の配列を指定することで、変数fitに傾きと切片の配列が返ります。
Polyfit関数
次元は$y=2x+1$のような1次式であるため1とする
次に、poly1dメソッドを使って回帰直線の式を求めます。といっても、poly1dメソッドは回帰分析に限ったものではなく、引数で指定した多項式のオブジェクトを構築するものです。
poly1dメソッド
引数に[1,2]を指定すると$x+2y$、[1,2,3]を指定すると$x^2+2X+3$のように、多項式を返す
ここではpoly1dにより、funcオブジェクトに$y=2x+1$の式がセットされます。そこでfuncの引数として$x$を指定すると$y$の予測値が計算されます。以降は、配列の引き算で残差を求め、最後にdataとして配列[0.6]をfuncに代入し予測値を計算します。
NumPyのpolyfitによる回帰式の計算
- fit = np.polyfit(x, y, 1)
- print('[傾き,切片]=', fit)
- func = np.poly1d(fit)
- predict_x = func(x)
- print('予測値=', predict_x)
- resudial_y = y-predict_x
- print('残差=', resudial_y)
- predict_d = func(data)
- print('x=[0,6] --> y=', predict_d)
これらの関数は、もっと奥深いものがあります。詳しくは次を参照してください。
scikit-learn
機械学習でよく使われるサイキットラーン(scikit-learn)による方法です。はじめにlr=LinearRegression()でscikit-learnにある回帰分析の機能を使うことを宣言します(LinearRegressionクラスのインスタンス化といいます)。次にfitメソッドでxとyの組み合わせについて学習をさせます。このときに、配列x:[1 4 3 5 2]をreshape関数で2次元の配列X[[1] [4] [3] [5] [2]]に変換します。もともとscikitlearnは説明変数が複数あることを前提としているためです。ここでは、X(大文字)としてxと区別します。以降は、predictメソッドで予測していきます。x=0,6の予測値も、[[0] [6]]のように変換してから計算します。
sklearnによる回帰式の計算
- from sklearn.linear_model import LinearRegression
- lr = LinearRegression()
- X = x.reshape((len(x), 1))
- lr.fit(X, y)
- print('傾き=',lr.coef_, '切片=', lr.intercept_)
- predict_x = lr.predict(X)
- print('予測値=', predict_x)
- resudial_y = y-predict_x
- print('残差=', resudial_y)
- D = data.reshape((len(data), 1))
- predict_d = lr.predict(D)
- print('x=[0,6] --> y=', predict_d)
傾き= [2.] 切片= 0.9999999999999982 予測値= [ 3. 9. 7. 11. 5.] 残差= [ 1. 1. -1. 0. -1.] x=[0,6] --> y= [ 1. 13.]
これまでに比べると少し複雑ですが、scikitlearnは、注目の機械学習が詰め込まれたモジュールなので、機械学習の考え方を垣間見ることができます。
statsmodelsによる方法
最後にstatsmodelsです。まず、add_constant関数で、配列x:[1 4 3 5 2]をX[[1. 1.] [1. 4.] [1. 3.] [1. 5.] [1. 2.]]に変換します。
これは重回帰分析を想定しているためです。
Scikitlearn と同じようにOLSクラス(Ordinary Least Squares regressionの略)でインスタンス化と、predictメソッドで予測します。ただし、predict_xを予測するときに、esults.predict(X)としても問題ありませんが、測定値についてはすでに学習済みなのでXに対する予測値にはfittedvaluesプロパテティ、残差についてはresidプロパティで計算することができます。
statsmodelsによる回帰式の計算
- import statsmodels.api as sm
- X = sm.add_constant(x)
- model = sm.OLS(y, X)
- results = model.fit()
- print('[切片,傾き]=', results.params)
- predict_x = results.fittedvalues # results.predict(X)でも可
- print('予測値=', predict_x)
- resudial_y = results.resid
- print('残差=', resudial_y)
- D = sm.add_constant(data)
- predict_d = results.predict(D)
- print('x=[0,6] --> y=', predict_d)
- print(results.summary())
[切片,傾き]= [1. 2.] 予測値= [ 3. 9. 7. 11. 5.] 残差= [ 1.00000000e+00 1.00000000e+00 -1.00000000e+00 1.77635684e-15 -1.00000000e+00] x=[0,6] --> y= [ 1. 13.]
statsModels は統計モデル用のライブラリで、このほかにも非常に多彩な機能があります。
まとめ
回帰直線の式を求める方法はさまざまですが、scikit-learn、statsmodelsについては、さらに高度な分析を想定しているので、少し手間が煩雑になっています。