相関係数の考え方

最小二乗法により回帰直線の式を求めることができます。しかし回帰直線を実務に役立てようとするとき、どれくらいあてはまりが良いかを確認しておく必要があります。予測値と測定値の間に差があまりにも大きい時は、説明変数を変えるなど他の方法を検討しなければなりません。回帰式の当てはまりの良さは散布図を見れば直感的にわかりますが、人によっても見方が異なってきます。そこで、当てはまりの良さを示す指標を計算し、ある一定の基準を満たしている場合、その回帰直線を利用するというようにしていく必要があります。

ここでは、相関の強さを示す指標として一番よく使われる相関係数について掘り下げていきます。

一次式による近似直線の表示

相関係数の計算

相関係数は、説明変数と目的変数が一直線上にきれいに正の相関を示している状態を1、逆に一直線上に負の相関を示しているときは-1とし、その間で回帰直線のあてはまりの良さ数値化するものです。相関関係が全く見られない場合はゼロとなります。このように相関係数は共分散と考え方が似ているので、実例をもとに共分散を求めるところからはじめます。

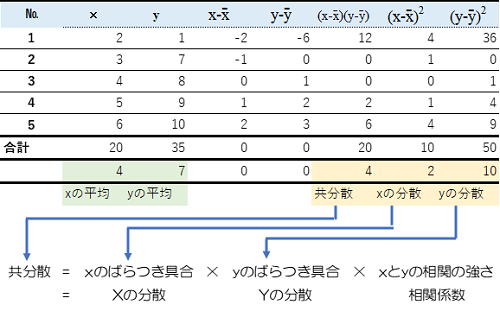
共分散は、$x$のばらつき具合×$y$のばらつき具合×相関の強さの掛け算です。

このため、$x$と$y$の相関の強さを計算するためには、共分散を$x$と$y$のばらつき具合の積で割ることにより計算できます。

具体的には次の式で計算することができます。

ここで、分子の共分散が$x$の偏差×$y$の偏差であるのに対し、分母は偏差の2乗通しの掛け算なので、バランスを取るため分散ではなく、その平方根である標準偏差を使うことに注意が必要です。

相関係数のめやす

相関係数はこれまで見てきたように$x$と$y$の相関の強さを表す指標です。それでは、相関係数がいくら以上であれば相関関係が強いと言えるでしょうか。もちろん、使用する目的によっても異なりますが、一般的には次の通りといわれています。

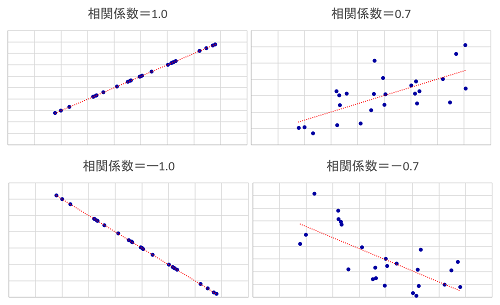
また、それぞれの相関係数に応じた散布図の一例を挙げます。相関係数を見るうえでの目安になると思います。

まとめ

非常におおざっぱではありましたが、相関係数についてご紹介しました。今後の展開に向けて数学的にもう少しきっちりと理解するとより一層理解が深まります。