相関係数を数学的にとらえる

回帰分析において相関係数はとても大切な役割を果たします。相関係数は数学的にどのような意味があるのか掘り下げてみます。

標準化

表のデータを売上実績と考えます。

図表１の左側の表（個数で計算）は、商品の個数を単位として平均、分散、標準偏差を計算しています。一方、この商品の単価を165円とします。右の表は、個数に165を掛けることにより金額をベースに、平均、分散、標準偏差を計算しています。2つの表は同じ内容のデータを分析しているのに、結果を見ると全く異なったものに見えてしまいます。そこで、単位の取り方が分析の結果に影響を及ぼすことがないようにするため、データを平均=0、分散=1のデータになるように変換します。このことを標準化（standardization）といいます。具体的には、各データに次の式をあてはめることにより標準化することができます。

標準化の計算

$\displaystyle標準化されたデータ=\frac{各データ-平均}{標準偏差}$

２つの表のうち標準化の列を見ると、同じ数字が並んでいます。例えば、Eの売上を標準化したデータで見ると0.424なので、平均から見て標準偏差の0.424倍だけ多い位置にいることがわかります。このように、標準化によって、データの分析において単位の取り方による影響を取り除くことができます。

相関係数と標準化

図表2のデータをもとに、相関係数を計算します。

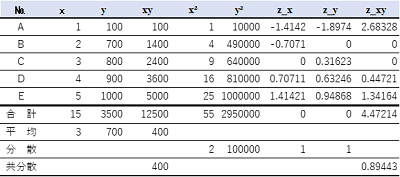
まず、相関係数に標準化の考え方をあてはめてみます。定義通りに相関係数を計算すると次の通りになります。

相関係数の計算

$\displaystyle 相関係数=\frac{xyの共分散}{xの標準偏差×yの標準偏差}$

$\displaystyle \frac{400}{\sqrt{2}\sqrt{100000}}\fallingdotseq 0.8944$

次に$z_x$、$z_y$は$x$、$y$それぞれを標準化されたデータで、その積が$z_xy$です。$z_xy$を合計してデータ数で割った数値は$z_x$、$z_y$の共分散になりますが、前に計算した相関係数と一致しています。このことから、相関係数は2つのデータを標準化した数値の共分散であると考えられます。標準化により、単位の取り方で分析結果が変わることを防ぐことができます。

数式で考える

$x$と$y$の標準化は次の式で計算することができます。

標準化

$\displaystyle z_{xi}=\frac{x_{i}-\bar{x}}{s_{x}}\qquad z_{yi}=\frac{y_{i}-\bar{y}}{s_{y}}$

相関係数を求める式を次のように変換すると、相関係数は標準化したデータの共分散であることがわかります。なお、$S_xy$は共分散、$S_x$、$S_y$は$x$、$y$それぞれの標準偏差です。

相関係数を求める式

$\displaystyle r_{xy} = \frac{S_{xy}}{S_x S_y} $

$\displaystyle = \frac{\sum(x_i-\bar{x})(y_i-\bar{y})/n}{S_x S_y} $

$\displaystyle =\frac{1}{n} \sum\left(\frac{x_{i}-\bar{x}}{s_{x}}\right)\left(\frac{y_{i}-\bar{y}}{s_{y}}\right) $

$=\displaystyle \frac{1}{n} \sum z_{xi} z_{yi}$

相関係数がとりうる値の範囲

相関係数が、平均0、分散1の2つの確率変数の共分散であることから、その値が-1から1の範囲であることは直感的には理解できますが、そのことを数学的に証明します。

このために、コーシー・シュワルツの不等式をご紹介します。

コーシー・シュワルツの不等式

$(x_1y_1+x_2y_2+\cdots+x_ny_n)^2 \le (x_1^2+x_2^2+\cdots+x_n^2)(y_1^2+y_2^2+\cdots+y_n^2)$

この不等式を変形すると次のようになります。

コーシー・シュワルツの不等式の変形

$\displaystyle \frac{(x_1y_1+x_2y_2+\cdots+x_ny_n)^2}{(x_1^2+x_2^2+\cdots+x_n^2)(y_1^2+y_2^2+\cdots+y_n^2)}\le 1$

分子が2乗を取ると

相関係数との対比

$-1\le\displaystyle \frac{x_1y_1+x_2y_2+\cdots+x_ny_n}{(x_1^2+x_2^2+\cdots+x_n^2)(y_1^2+y_2^2+\cdots+y_n^2)}\le 1$

等号は次の場合に成り立ちます。

等号が等しい場合

$\displaystyle\frac{y_1}{x_1}=\frac{y_2}{x_2}=\cdots=\frac{y_n}{x_n}$

ところで、$x_1,x_2, \cdots x_n\quad ,y_1,y_2\cdots y_n$をx,yの偏差（各データ-平均）とすると、式の分子はxとyの積和、分母はxの偏差平方和×yの偏差平方和となるので、商は相関係数になります。

コーシー・シュワルツの不等式は、変数が2つの場合には次の通り証明できます。

変数が2つの場合

$(x_1y_1+x_2y_2)^2 \le (x_1^2+x_2^2)(y_1^2+y_2^2)$

$(x_1^2+x_2^2)(y_1^2+y_2^2)-(x_1y_1+x_2y_2)^2$

$=(x_1^2y_1^2+x_1^2y_2^2+x_2^2y_1^2+x_2^2y_2^2)-(x_1^2y_1^2+2x_1x_2y_1y_2+x_2^2y_2^2)$

$=x_1^2y_2^2-2x_1x_2y_1y_2+x_2^2y_1^2$

$=(x_1y_2-x_2y_1)^2 \ge 0$

等号は次の場合に成り立ちます。

等号が等しい場合

$\displaystyle\frac{y_1}{x_1}=\frac{y_2}{x_2}$

また、変数が3つの場合には、次の通り証明できます。

変数が3つの場合

$(x_1y_1+x_2y_2+x_3y_3)^2 \le (x_1^2+x_2^2+x_3^2)(y_1^2+y_2^2+y_3^2)$

$(x_1^2+x_2^2+x_3^2)(y_1^2+y_2^2+y_3^2)-(x_1y_1+x_2y_2+x_3y_3)^2$

$=x_1^2(y_2^2+y_3^2)+x_2^2(y_1^2+y_3^2)+x_3^2(y_1^2+y_2^2)-2(x_1x_2y_1y_2+x_2x_3y_2y_3+x_3x_1y_3y_1)$

$=(x_1y_2-x_2y_1)^2+(x_2y_3-x_3y_2)^2+(x_1y_3-x_3y_1)^2 \ge 0$

等号が成り立つのは次の場合になります。

等号が等しい場合

$\displaystyle \frac{y_1}{x_1}=\frac{y_2}{x_2}\qquad\frac{y_2}{x_2}=\frac{y_3}{x_3}\qquad \frac{y_3}{x_3}=\frac{y_1}{x_1}$

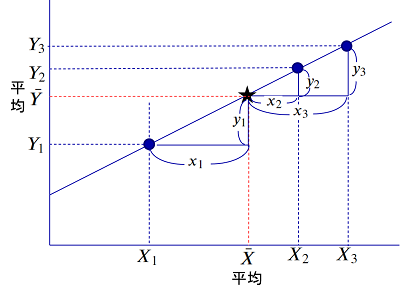
&つまり、$x$と$y$の比が等しい場合です。

$\displaystyle \frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{y_3}{x_3}$

この式で、図のように$x_i$と$y_i$の比が等しいということは、グラフのように点がすべて一直線に並んでいることを示しています。これは、相関係数が1で正の相関のケースです。

まとめ

次に向けて、回帰分析の各数値の間の関係を知る必要があります。

回帰分析の特徴を直感的にとらえる