Excelで回帰係数、相関係数を計算する
最小二乗法による式や相関係数の計算においても、Excelは強力な機能を持っています。
EXCELの表と列の意味
各セル(列)の概要を確認します。
| 列 | 計算式 | 概 要 |
|---|---|---|
| C | $x$ | 説明変数$x$の値を入力し、11行目に合計、12行目に平均$\bar{x}$を計算 |
| D | $y$ | 目的変数$y$の値を入力し、11行目に合計、12行目に平均$\bar{y}$を計算 |
| E | $x-\bar{x}$ | $x$と平均との偏差。合計すると0になる。 |
| F | $y-\bar{y}$ | $y$と平均との偏差。合計すると0になる。 |
| G | $(x-\bar{x})^2$ | $x$の偏差の2乗。G11で合計した値が偏差平方和。G12はG11÷データ数nより分散を計算 |
| H | ($y-\bar{y})^2$ | $y$の偏差の2乗。H11で合計した値が偏差平方和。H12はH11÷データ数nより分散を計算 |
| I | $(x-\bar{x̄})(y-\bar{y})$ | $x$の偏差と$y$の偏差の積。I11の合計が積和、I12でI11をデータ数で割ることにより共分散を計算 |
| J | $xy$ | $x$と$y$の積。J11の合計値を共分散の簡便法の計算で使用。 |
| K | $x^2$ | $x$の2乗。K11の合計値は$x$の偏差平方和、分散の簡便法の計算で使用 |
| L | $y^2$ | $y$の2乗 。L11の合計値は$y$の偏差平方和、分散の簡便法の計算で使用 |
各数値の計算
偏差平方和($T_{xx}$、$T_{yy}$)分散($S_{xx}$、$S_{yy}$)
図表1にもとづき式を入力し、C6:D10にデータを入力すると図表2のようになります。
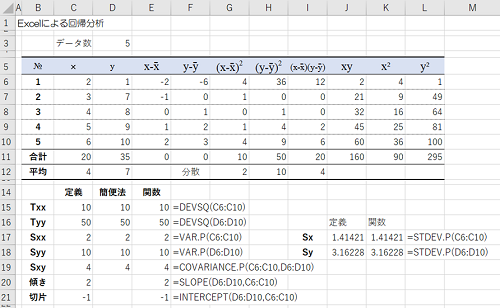
すでにG11で計算した$x$の偏差平方和$T_{xx}$をセルC15で表示しています。D15では簡便法で計算しています(=K11-C11^2/D3)。また、E15では偏差平方和をDEVSQ関数で計算しています。
DEVSQ関数
ちなみに偏差平方和は英語ではDeviation sum of squaresであり、Deviationは偏差をいいます。
またC17では分散の値を表示していますが、これもすでにG12で計算済です。E17では分散をVAR.P関数で計算しています。さらに分散の平方根が標準偏差でありJ17その計算をしています。K18ではSTDEV.P関数を使い標準偏差を計算しています。
VAR.P関数
STDEV.P関数
なお、VAR.P関数、STDEV.P関数はデータを母集団として偏差平方和をデータ数nで割って計算します。いっぽう、データが標本の場合にはデータ数n$-$1で割る必要があります。この場合にはVAR.S関数、STDEV.S関数を使います。
積和、共分散($T_{xy}$)
積和については、I11で計算しており、これをデータ数で割ったものがI12の共分散になります。この共分散はC19で表示するとともにD19では簡便法で計算しています(=(J11-C11*D11/D3)/D3)。
積和に関する関数は無く、共分散はE19でCOVARIANCE.P関数を使って計算します。
COVARIANCE.P関数
なお、COVARIANCE.P関数はデータを母集団として偏差平方和をデータ数nで割って計算します。いっぽう、データが標本の場合にはデータ数n$-$1で割る必要があります。この場合にはCOVARIANCE.S関数を使います。
covarianceは英語で共分散を指します。
回帰曲線の傾き(SLOPE、INTERCEPT)
回帰曲線の傾きは$S_{xy}/S_{xx}$で計算することができます。そこで、この計算をC20で行っています(=C19/C17)。
SLOPE関数
引数は(目的変数、説明変数)の順番であることに注意
INTERCEPT関数
引数は(目的変数、説明変数)の順番であることに注意
英語では傾きはSLOPE、切片は INTERCEPTで関数名もそのままです。
まとめ
EXCELの回帰分析における機能のうち、きわめて基本的なものを挙げました。しかし、まだまだ豊富な機能がEXCELには備わっています。