回帰係数の傾き、分散を数学的に計算する

使用する変数と計算の前提

使う変数の概要

回帰分析における傾き、切片（回帰係数）の期待値と分散を数学的に求めます。計算で使う主な変数は次の通りです。ここでの特徴として、測定データそのものの値は大文字で表すこととし、説明変数は$X$の目的変数は$Y$とします。一方、平均との差である偏差は小文字で表すこととし、それぞれ$x$、$y$とします。

用語 記号 意　　　　　　味
データ数 $n$ 回帰分析をするにあたり測定したサンプルの数
測定値 $X_i,Y_i$ サンプルを測定した結果、得られたi番目のデータ
予測値 $\hat{Y_i}$ サンプルから導かれた回帰直線の式によって、$X_i$から計算された$Y_i$の値
平均 $\bar{X},\bar{Y}$ 平均　$\bar{X}=\sum X_i / n$、$\bar{Y}=\sum Y_i / n$で計算
真の傾き $\beta$ 母集団の回帰直線の傾き
傾きの推定量 $\hat{\beta}$ 回帰分析によって導かれた回帰直線の式の傾きの推定量
真の切片 $\alpha$ 母集団の回帰直線の切片
切片の推定量 $\hat{\alpha}$ 回帰分析によって導かれた回帰直線の式の切片の推定量
誤差 $\epsilon$ 母集団の$Y_i$と回帰直線により計算した$Y$の値の差
残差 $e_i$ サンプルにおける測定値$y_i$と予測値$\hat{y_i}$の差　
重み $w_i$ $\hat{\beta}$を計算する際に各$Y_i$に掛ける重み
回帰係数 $\alpha,\beta$ 回帰直線の式での傾きと切片を合わせたもの

想定する回帰直線の式

回帰分析で想定する回帰直線の基本的な式を確認します。回帰分析では、目的変数$Y_i$を予測、説明するため、傾き$\beta$と切片$\alpha$を使い、説明変数$X_i$が決まると、$\alpha+\beta X_i$の式に代入して$Y_i$の値を推定します。この推定値は、大体これくらいになることが期待されるという意味で、$Y_i$の期待値といい、$ E[Y_i] $で表します。

\mathrm E[Y_i]=\alpha+\beta X_i\tag{前提1}$

しかし、現実的にはいろいろな要因から$Y_i$の実際の値と期待値の間では誤差$\epsilon$が生じます。$Y_i$の期待値$ E[Y_i] $と実際の$Y_i$は次の関係にあります。

Y_i=\mathrm E[Y_i]+\epsilon_i\tag{前提2}$

このため、回帰分析では次の式を基本的な式として想定します。

Y_i=\alpha+\beta X_i+\epsilon_i\quad i=1,2,\cdots ,n\tag{前提3}$

前提となる仮定

次に、回帰直線の式の傾き、切片の期待値、分散を求めるにあたって、前提となる仮定をまとめておきます。

誤差の期待値は0である

回帰直線は各データの中間を貫くように引くので、誤差はプラスになる場合もマイナスになる場合もあり、全体を均してみるとプラスマイナスがバランスして期待値は0になると仮定します。

\mathrm E[\epsilon_i]=0\tag{仮定1}$

誤差$\epsilon$の分散$\sigma^2$は$X_i$の大きさにかかわらず一定である

$\epsilon$の分散は、$E[\epsilon_i-\mathrm E[\epsilon_i]]^2$で計算しますが、$\mathrm E[\epsilon_i]=0$なので、$\mathrm E[\epsilon^2]$と等しくなります。$X_i$の値に応じて$Y_i$も変動しますが、$Y_i$の大きさに関わらず分散は一定であると仮定しており、その値を$\sigma^2$とします。

\mathrm V[\epsilon_i]=E[\epsilon_i-\mathrm E[\epsilon_i]]^2=\mathrm E[\epsilon_i^2]=\sigma^2\tag{仮定2-1}$

同じように、$Y_i$の分散（$X_i$に対する$Y_i$の期待値との間のばらつき）は$\epsilon$の分散と同じことになり、やはり$\sigma^2$となります。

\mathrm V[Y_i]=E[Y_i-\mathrm E[Y_i]]^2=\mathrm E[\epsilon_i^2]=\sigma^2\tag{仮定2-2}$

誤差項の分散は独立である。

誤差はいろいろな要因で発生するので、その出方はばらばらであり、前の点が期待値より大きかったから、今回は少し小さめにしようというような意図は働かないということです。数学的には、異なるデータ間の誤差の共分散は0であることを示しています。

cov[\epsilon_i \epsilon_j]=\mathrm E[\epsilon_i \epsilon_j]=0\quad i\ne j \quad i=1,2,\cdots ,n\tag{仮定3}$

$X$は確率変数ではない

説明変数$X$を広告件数、目的変数$Y$を新規顧客数とした場合、同じだけ広告を打っても、新規顧客数が同じになるとは限りません。この時の目的変数のばらつき（誤差）を$\epsilon$とすると、$Y$や$\epsilon$は$X$が与えられても、何パーセントの確率でこの範囲としか決められないので確率変数となります。一方、$X$は一度、これだけ広告を打つと決めてしまえば確定するので、定数、非確率変数といわれています。確率変数と定数とでは期待値や分散を計算するときに扱いが異なってきます。たとえば確率変数を$P$、定数を$a$、$b$とした場合、期待値は次の通りになります。

E[aP+b]=aE[P]+b$

期待値を求める場合、定数は$E[ ]$の外に出すことができます。一方、分散は少し複雑です。

V[aP+b]=a^2V[P]$

分散は、各データを2乗して計算するので、確率変数にある数を掛ける場合、$V[ ]$から出すことはできますが、このときには2乗する必要があります。一方、分散はそもそもばらつきを表しているので、$b$はばらつかない数なので計算の対象に含まれません。

傾きの期待値と分散の計算

回帰係数の計算の考え方

回帰分析の直線の傾きは次の通り計算することができます。

回帰直線の傾きの計算
\displaystyle\hat{\beta}=\frac{T_{xy}}{T_{xx}}=\frac{\displaystyle\sum_{i=1}^n{(X_i-\bar{X})(Y_i-\bar{Y})}}{\displaystyle\sum_{i=1}^n(X_i-\bar{X})^2}=\frac{\displaystyle\sum_{i=1}^nx_iy_i}{\displaystyle\sum_{i=1}^nx_i}$

このうち$x_i$は確率変数ではなく定数なので、$x_i$に関わる部分だけを取り出して、$w_i$を定義します。

\displaystyle　w_i=\frac{(X_i - \bar{X})}{\displaystyle\sum_{i=1}^n(X_i - \bar{X})^2}=\frac{x_i}{\displaystyle\sum_{i=1}^nx_i^2}$

$w_i$は重み（weight）という意味で、$\hat{\beta}$は次のように表現することができます。

\displaystyle \hat{\beta}=\sum_{i=1}^nw_i y_i$

この$w_i$は$x_i$が定数であることから定数となり、次の通りとても面白い性質があります。

\displaystyle \sum_{i=1}^n w_i=0\tag{1-1}$
\displaystyle\sum_{i=1}^n w_i X_i=\sum_{i=1}^n w_i x_i=1\tag{1-2}$
\displaystyle \sum_{i=1}^n w_i^2=\frac{1}{\sum_{i=1}^n(x_i)^2}\tag{1-3}$

図表1でこれらの式を検証しています。

式1－1については、H列で$w_i$の合計が0であることがわかります。

式1－2については、J列で$w_i X_i$、K列で$w_i x_i$の合計が1であることがわかります。

式1－3については、I列の$w_i^2$の合計がF列の$x_i^2$の合計の逆数になっていることがわかります。

さらに面白いことに、$\bar{Y}$は定数で、式(1-1)であることから次のことがいえます。

\displaystyle \hat{\beta}=\sum_{i=1}^nw_iy_i=\sum_{i=1}^nw_i(Y_i-\bar{Y})=\sum_{i=1}^nw_iY_i-\bar{Y}\sum_{i=1}^nw_i=\sum_{i=1}^nw_iY_i\tag{2}$

となります。

$\hat{\beta}$は、サンプルの目的変数$Y_i$（またはその偏差$y_i$）一つ一つが何らかの影響を与えて決められます。ただ、どの点も同じだけ影響を与えているわけでなく、重みが微妙に異なります。具体的にはH列で$w$の値を見ると、平均から離れている点の方がテコの考え方で絶対値が大きくなります。

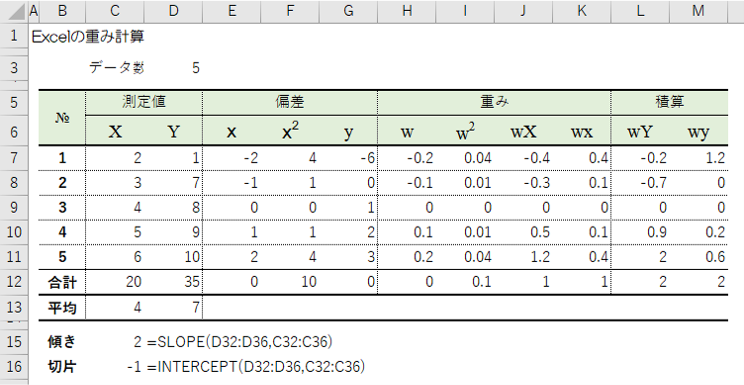
重みづけから傾きの予測値を計算
重みづけから傾きの予測値を計算

列 概要
C 説明変数のデータを入力し合計と平均を計算します。
D 目的変数のデータを入力し合計と平均を計算します。ここからセルC15でslope関数で傾きを計算。結果が2であることを確認します。
E Xの偏差$x_i=(X-\bar{X})$を計算します。合計すると0であることを確認します。
F Xの偏差の2乗を計算して合計します。合計すると10であることを確認します。
G Yの偏差($y_i=Y-\bar{Y})$を計算します。合計すると0であることを確認します。
H 重み$w_i$を計算します。$w_i$は、合計は0ですが、平均から離れるほど絶対値が大きくなることを確認します。
I 重み$w_i$に$X_i$の測定値の積を計算し合計します。合計が0になることを確認します。
J 重み$w_i$に$x_1$の測定値の積を計算し合計します。合計が0になることを確認します。
k 重み$w_i$の2乗を求め合計します。合計がセル$x^2$の合計値の逆数であること確認します。
L 重み$w_i$×目的変数$Y$を計算して合計します。合計は2と傾きの予測値と等しいことを確認します。
M 重み$w_i$×目的変数の偏差$y$を計算して合計します。合計は2と傾きの予測値と等しいことを確認します。

傾きの期待値と分散の計算

このことから$\hat{\beta}$は次の通り表現することができます。

\displaystyle \hat{\beta}=\sum_{i=1}^nw_iY_i$
\displaystyle =\sum_{i=1}^nw_i(\alpha+\beta X_i+\epsilon_i)$
\displaystyle =\alpha\sum_{i=1}^nw_i+\beta \sum_{i=1}^nw_iX_i+\sum_{i=1}^nw_i\epsilon_i$
=\displaystyle \beta+\sum_{i=1}^n w_i \epsilon_i$

2行目は（前提3）より$Y_i$を展開することができます。また、式(1-1)より$\sum w_i=0$、式(1-2)より$\sum w_iX_i=0$なので、3行目の式は簡単に整理することができます。

このため、$\hat{\beta}$の期待値は次の通り計算することができます。

\displaystyle E[\hat{\beta}] =E\left[\beta+\sum_{i=1}^n w_i \epsilon_i\right]=\beta + \sum_{i=1}^n{w_iE[\epsilon_i]}=\beta $

ここで、$w_i$は定数なので$E[ ]$の外に出すことができ、仮定1より$[\epsilon]=0$

となるためです。さらに、$\hat{\beta}$の分散は次の通り計算することができます。

V[\hat{\beta}]=E[(\hat{\beta}-E[\hat{\beta}])^2]$
\displaystyle =E[(\hat\beta-\beta)^2]=E\left[\left(\sum_{i=1}^n w_i \epsilon_i\right)^2\right]$
\displaystyle =\sigma^2\sum_{i=1}^n w_i^2=\frac{\sigma^2}{\displaystyle\sum_{i=1}^n(X_i-\bar{X})^2}=\frac{\sigma^2}{\displaystyle\sum_{i=1}^n x_i^2}$

まとめると、次の通りになります。

\displaystyle\hat{\beta}=\frac{T_{xy}}{T_{xx}}\sim N\left(\beta,\dfrac{\sigma^2}{\sum_{i=1}^n(X_i-\bar{X})^2}\right)= N\left(\beta,\dfrac{\sigma^2}{\sum_{i=1}^n x_i^2}\right)=N\left(\beta,\dfrac{\sigma^2}{T_{xx}}\right)$

切片の期待値と分散の計算

切片$\alpha$については、導くことができます。

切片の期待値の計算
\bar{Y}=\alpha+\beta\bar{X}+\bar{u}$
\hat{\alpha}=\bar{Y}-\beta\bar{X}$
=\alpha-(\hat{\beta}-\beta) \bar{X}+\bar{u}$
\mathrm{E}(\hat{\alpha})=\alpha-\mathrm{E}(\hat{\beta}-\beta) \bar{X}+\mathrm{E}(\bar{u})=\alpha$

同様に、分散についても次の通り計算することができます。

切片の分散の計算
\mathrm{V}(\hat{\alpha}) =\mathrm{E}(\hat{\alpha}-\alpha)^{2}$
=\mathrm{E}(-(\hat{\beta}-\beta) \bar{X}+\bar{u})^{2} $
=\bar{X}^{2} \mathrm{E}(\hat{\beta}-\beta)^{2}-2 \bar{X} \mathrm{E}((\hat{\beta}-\beta) \bar{u})+\mathrm{E}\left(\bar{u}^{2}\right)$
=\sigma^{2}\left(\frac{\bar{X}^{2}}{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}}+\frac{1}{n}\right)$

このことから、切片$\alpha$は次の分布に従います。

\displaystyle\hat{\alpha}=\frac{T_{xy}}{T_{xx}}\sim N\left(\alpha, \frac{\bar{X}^{2}}{\sum_{i=1}^{n}x_i^{2}}+\frac{1}{n} \right)$

$w_i$に関する式の導出

式1-1~1-3の導出は次の通りです。まず、$\sum x_i$（$X_i$の偏差の合計）は0になります。

\displaystyle \sum x_i=\sum(X_i-\bar{X})=0$

そこで、式1-1は分母が0になるので0になります。

\displaystyle \sum w_i=\frac{\displaystyle \sum x_i}{\displaystyle\sum nx_i^2}=0\tag{1-1}$

式1-1および$\bar{X}$が定数であることから$\sum w_i\bar{X}$=0になるので、$\sum w_iX_i=\sum w_ix_i$になります。

\displaystyle \sum w_iX_i=\sum w_iX_i-\sum w_i\bar{X}=\sum w_i(X_i-\bar{X})=\sum w_ix_i$

このことから式1-2のとおり$\sum w_ix_i$は、分母と分子が等しくなるので1になります。

\displaystyle \sum w_ix_i=\frac{\displaystyle \sum x_i}{\displaystyle\sum x_i^2}x_i=\frac{\displaystyle \sum x_i^2}{\displaystyle\sum x_i^2}=1\tag{1-2}$

最後に、$w_i^2$は、次の通り$\frac{1}{\sum x_i^2}$と等しくなり式1-3の通りになります。

\displaystyle \sum w_i^2=\left(\frac{1}{\sum x_i^2}\right)^2 \sum x_i^2=\frac{1}{\sum x_i^2}\tag{1-3}$